Sei $I=[0,1]$, $C(I)$ der Raum der stetigen Funktionen auf $I$ mit der Norm $\norm f\colon=\sup\{|f(x)|:x\in I\}$. Weiters sei $\vp(x)=x^+\colon=\max\{x,0\}$ und für $y\in I$: $L_x\vp(y)\colon=\vp(y-x)$ die Translationen von $\vp$. Dann ist der von der konstanten Funktion $1$ und den Funktionen $L_x\vp$, $x\in I$, aufgespannte Unterraum $E$ von $C(I)$ dicht in $C(I)$.
1. Sei $f\in C^2(\R)$. Nach der Taylor-Formel gilt für alle $y > 0$:
$$
f(y)
=f(0)+f^\prime(0)y+\int_0^y(y-t)^+f^\dprime(t)\,dt
=a+by+\int_0^y(y-t)^+f^\dprime(t)\,dt
$$
und somit liegt $f|[0,1]$ im Abschluß von $E$; ferner ist mit $\mu(a,b]=D_+f(b)-D_+f(a)$ - d.h. falls $f\in C^2$: $\mu(a,b]=\int_a^b f^\dprime(y)\,dy$:
$$
f(y)
=a+by+\int_0^y(y-t)^+\,\mu(dt)~.
$$
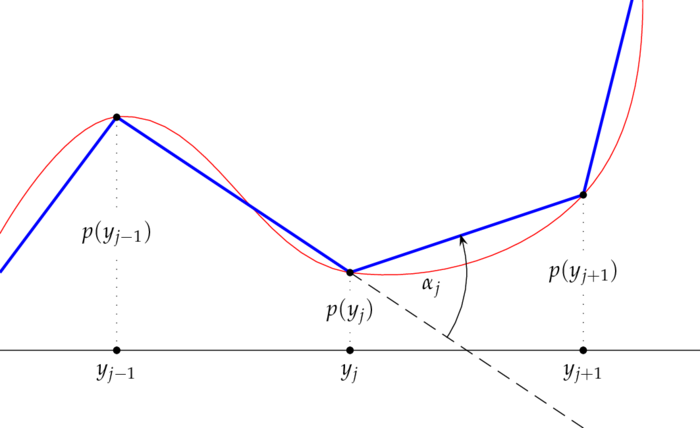
2. Beweis durch Zeichnung: Sei $f\in C(I)$ und $p$ ein Polygonzug, d.h. es gibt eine Zerlegung $0=y_0 < y_1 < \cdots < y_{n-1} < y_n=1$, so daß erstens $p(y_j)=f(y_j)$, zweitens $p$ auf allen Intervallen $[y_j,y_{j+1}]$ affin ist, also von der Form $p(y)=a_jy+b_j$, und drittens $\norm{f-p}$ beliebig klein. Dann ist
$$
p(y)=p(0)+\l_0\vp(y)+\sum_{j=1}^{n-1}\l_j L_{y_j}\vp(y)
$$
mit $\l_0=(p(y_1)-p(y_0))/(y_1-y_0)$ und für $j > 0$: $\l_j=\tan(\a_j)$, wobei die Winkeln $\a_j$ wie in folgender Grafik definiert sind.