Sei $1/2 < a < 1$ und $f_a(z)\colon=(1+z^2)^{-a}\colon=\exp(-a\log(1+z^2))$.
Zeigen Sie, daß $f_a$ auf $\O\colon=\C\sm\{it:t\in\R\sm(-1,1)\}$
differenzierbar ist und daß
$$
\int_\R f_a(x)\,dx
=\sin(a\pi)\int_0^\infty\frac{dt}{t^a\sqrt{1+t}}~.
$$
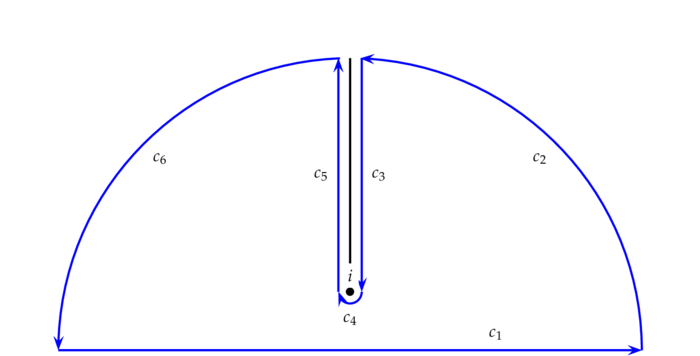
Wir betrachten für $n\to\infty$ und $\e\dar0$ folgende Wege: $c_1$ sei die
Strecke von $-n$ nach $n$, $c_2$ der Viertelkreisbogen von $n$ nach $in+\e$,
$c_3$ die Strecke von $in+\e$ nach $i+\e$, $c_4$ der negativ durchlaufene
Halbkreis von $i+\e$ nach $i-\e$, $c_5$ die Strecke von $i-\e$ nach $in-\e$
und schließlich $c_6$ der Viertelkreisbogen von $in-\e$ nach $-n$. Da
$$
\lim_{n\to\infty}\int_{c_2}f_a(z)\,dz
=\lim_{n\to\infty}\int_{c_6}f_a(z)\,dz
=\lim_{\e\dar0}\int_{c_4}f_a(z)\,dz=0
$$
sowie mit $c_3^{-1}(t)=i\sqrt{1+t}+\e$, $t\in\R$:
$$
\lim_{\e\dar0}\int_{c_3}f_a(z)\,dz
=-\tfrac12i\int_0^\infty\frac{e^{-a(\log(-t)+i\pi)}}{\sqrt{1+t}}\,dt
=-\tfrac12ie^{ia\pi}\int_0^\infty\frac{dt}{t^a\sqrt{1+t}}\,dt
$$
und analog:
$$
\lim_{\e\dar0}\int_{c_5}f_a(z)\,dz
=\tfrac12ie^{-ia\pi}\int_0^\infty\frac{dt}{t^a\sqrt{1+t}}\,dt
$$
Nach dem Cauchyschen Integralsatz folgt daher:
$$
\lim_n\int_{c_1}f_a(z)\,dz
=\tfrac12i(e^{ia\pi}-e^{-ia\pi})\int_0^\infty\frac{dt}{t^a\sqrt{1+t}}\,dt
$$