Zeigen Sie, daß die Fourier-Transformierte der Funktion $f(x)\colon=1/\sinh(x)$ gegeben ist durch
$$
\wh f(y)\colon=\frac1{\sqrt{2\pi}}\pv\int_\R \frac{e^{-ixy}}{\sinh(x)}\,dx
=-\frac{i}{\sqrt{2\pi}}\int_\R \frac{\sin(xy)}{\sinh(x)}\,dx
=-i\sqrt{\pi/2}\tanh(\pi y/2)~.
$$
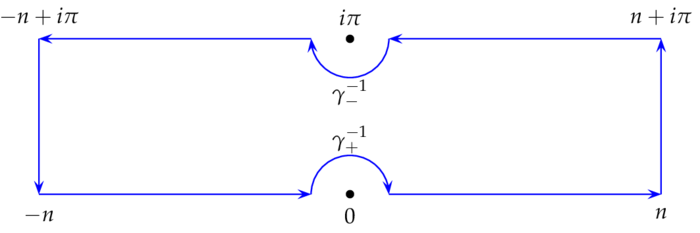
Wir integrieren über das Rechteck mit den Eckpunkten $-n,n,n+\pi i,-n+\pi i$.
In diesem Bereich hat die Funktion $f(z)=e^{-izy}/\sinh(z)$ nur zwei Pole: $0$ und $i\pi$, die beide auf dem Integrationsweg liegen; ihre Residuen sind
$$
\Res(0,f)=1\quad\mbox{bzw.}\quad
\Res(i\pi,f)=-e^{\pi y}~.
$$
Nach dem Residuensatz erhalten wir also mit $n\to\infty$ und $\g_+(t)=re^{it}$, $t\in(0,\pi)$ bzw. $\g_-(t)=i\pi+re^{it}$, $t\in(\pi,2\pi)$:
\begin{eqnarray*}
0
&=&\pv\int_\R f(x)\,dx-\lim_{r\dar 0}\int_{\g_+}f(z)\,dz
-\pv\int_\R f(x+i\pi)\,dx-\lim_{r\dar 0}\int{\g_-}f(z)\,dz\\
&=&(1+e^{\pi y})\pv\int_\R\frac{e^{-ixy}}{\sinh(x)}\,dx
-i\pi(\Res(0,f)+\Res(i\pi,f))
\end{eqnarray*}
Es folgt:
$$
\pv\int_\R\frac{e^{-ixy}}{\sinh(x)}\,dx
=i\pi\frac{1-e^{\pi y}}{1+e^{\pi y}}
=-i\pi\tanh(\pi y/2)~.
$$