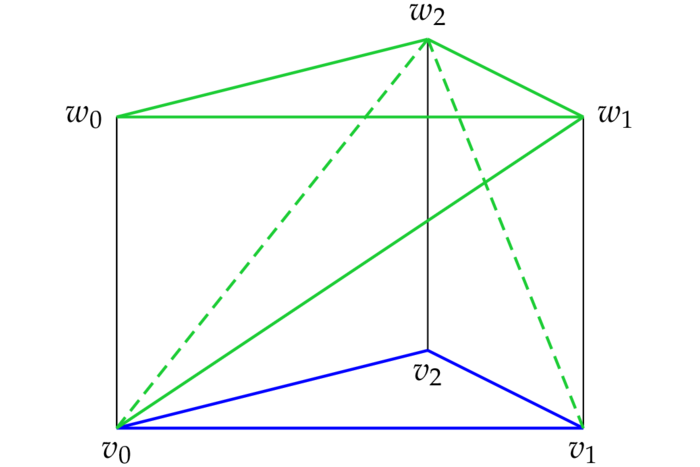
Prove that for any simplex $S$ in $\R^n$ the prism $S\times[0,1]$ is the disjoint union of $n+1$ simplices with pairwise disjoint interior, all the same volume $\vol n(S)/(n+1)$.
Suppose $e_0,\ldots,e_n$ are the vertices of an $n$-simplex $S$ in $\R^n$; put
$$
v_k\colon=(e_k,0)\in\R^{n+1},
\quad\mbox{and}\quad
w_k\colon=(e_k,1)\in\R^{n+1}~.
$$
Define $\vp_{-1},\vp_0,\ldots,\vp_n:S\rar[0,1]$ by
$$
\vp_k(\sum t_je_j)\colon=\sum_{j > k}t_j~.
$$
For $j\leq k$ we have: $\vp_k(e_j)=0$ and for $j > k$: $\vp_k(e_j)=1$. As $\vp_k$ is an affine function its graph $\{(x,\vp_k(x)):x\in S\}$ coincides with
$$
\convex{v_0,\ldots,v_k,w_{k+1},\ldots,w_n}~.
$$
Since $\vp_n=0$, $\vp_{-1}=1$ and $\vp_k\leq\vp_{k-1}$ the sets
$$
S_k=\{(x,t)\in S\times I:\,\vp_k(x)\leq t\leq\vp_{k-1}(x)\}
$$
have pairewise disjoint interior and their union is $S\times I$. Moreover
$$
S_k=\convex{v_0,\ldots,v_k,w_k,\ldots,w_n}~.
$$
By Cavalieri's principle the volume of $S_k$ coincides with the volume of the pyramid over $S$ with vertex $w_k$, which is $\vol n(S)/(n+1)$.