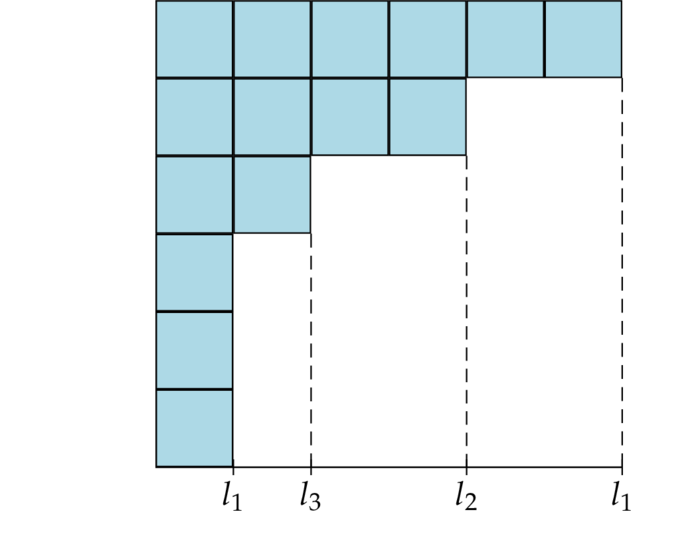
The dimension of the irreducible representation with character $\chi_p$ is given by
$$
\chi_p(e)
=\frac{n!}{\l_1!\cdots\l_k!}
\prod_{i < j}(\l_i-\l_j)~.
$$
Cf.
For any transposition $\t$ we have (cf.
W. Fulton and J. Harris p.52):
$$
\frac{\chi_p(\t)}{\chi_p(e)}
=\frac1{n(n-1)}\sum_{j=1}^r(b_j(b_j+1)-a_j(a_j+1))~.
$$