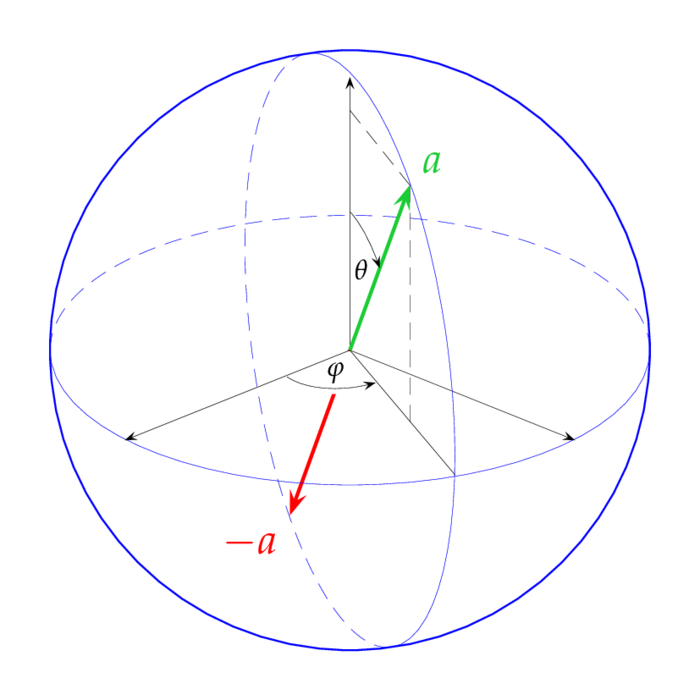
We already know that $\exp(-itS_a)\in\SU(2)$ and that $\pm1/2$ are the eigen values of $S_a$ , cf. exam. So let's compute the eigen-vectors: $x=x_1e_1+x_2e_2$ is a normalized eigen-vector of $S_a$ for the eigen-value $1/2$ iff $$ |x_1|^2+|x_2|^2=1 \quad\mbox{and}\quad (a_3-1)x_1+(a_1-ia_2)x_2=0~. $$ which implies $$ \frac{x_2}{x_1}=\frac{1-a_3}{a_1-ia_2} =\frac{1-\cos\theta}{\cos\vp\sin\theta-i\sin\vp\sin\theta} =\frac{e^{i\vp}\sin(\theta/2)}{\cos(\theta/2)}~. $$ Thus the eigen-vector of $S_a$ for the eigen-value $1/2$ is given by $$ x=e^{-i\vp/2}\cos(\theta/2)e_1+e^{i\vp/2}\sin(\theta/2)e_2 $$ Analogously the eigen-vector of $S_a$ for the eigen-value $-1/2$ is given by: $$ y=-e^{-i\vp/2}\sin(\theta/2)e_1+e^{i\vp/2}\cos(\theta/2)e_2~. $$
