Exam

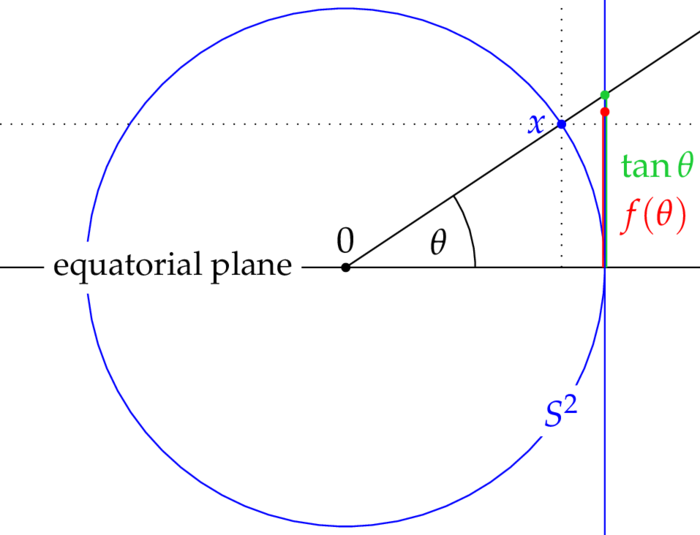
Find a smooth increasing function $f:(-\pi/2,\pi/2)\rar\R$, $f(0)=0$, such that the Mercator map $F:(M,g)\rar(-\pi,\pi)\times\R$, $(\vp,\theta)\colon=(\vp,f(\theta))$ is conformal. Here $g$ denotes the Riemannan metric $g$ of exam and $(-\pi,\pi)\times\R$ carries the canonical Euclidean metric. The Mercator map is also called cylindrical projection and has been rampant in navigation. Remarkably, the problem of finding an appropriate function $f$ was solved in 1668 by James Gregory and two years later by Isaac Barrow, at a time when calculus was not yet well established.

We are looking for a smooth increasing function $f$ such that $F:M\rar(-\pi,\pi)\times\R$ is conformal with respect to the pull back metric $g$ on $M$ and the euclidean metric on $(-\pi,\pi)\times\R$. The Jacobi matrix $DF(\vp,\theta)$ of $F$ is given by $$ \left(\begin{array}{cc} 1&0\\ 0&f^\prime(\theta) \end{array}\right)~. $$ Denoting the coordinates on $(-\pi,\pi)\times\R$ by $\phi$ and $z$ we thus get: $TF(E^\vp)=E^\phi$ and $TF(E^\theta)=f^\prime(\theta)\,E^z$ with Gramian $$ \left(\begin{array}{cc} 1&0\\ 0&f^{\prime2}(\theta) \end{array}\right)~. $$ As the Gramian of $E^\vp$ and $E^\theta$ on $M$ is $$ \left(\begin{array}{cc} \cos^2\theta&0\\ 0&1 \end{array}\right)~. $$ we infer that $F$ is conformal with scaling function $h > 0$ if $h^2\cos^2\theta=1$ and $h^2=f^{\prime2}$, i.e. $$ f^\prime(\theta)=h(\theta)=\frac1{\cos\theta} \quad\mbox{and thus}\quad f(\theta)=\frac12\log\frac{1+\sin\theta}{1-\sin\theta}~. $$ Neglecting a few points we may identify $(M,g)$ with $S^2$ by exam and $(-\pi,\pi)\times\R$ with the cylinder $S^1\times\R$. Since $|f(\theta)|\leq|\tan\theta|$ the point $(\vp,f(\theta))\in S^1\times\R\sbe\R^3$ is a little bit closer to the image $S^1\times\{0\}$ of the equator than the point $(\vp,\tan\theta)$, which is just the intersection of the cylinder $S^1\times\R$ and the one dimensional subspace generated by the point $x$ on the sphere $S^2$ with longitude $\vp$ and latitude $\theta$.