← Inner Products → Tensors
What should you be acquainted with? 1. Linear Algebra in particular: inner product spaces, also called spaces with a Euclidean product over the real numbers. 2. Only the last section on conformal mappings requires some knowledge from analysis.

Lorentz Spaces and Relativity

Lorentz Spaces

Cf. students version in german

Time-, space- and light-like vectors

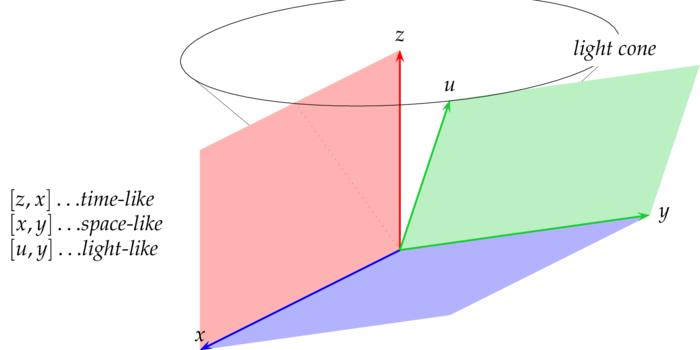
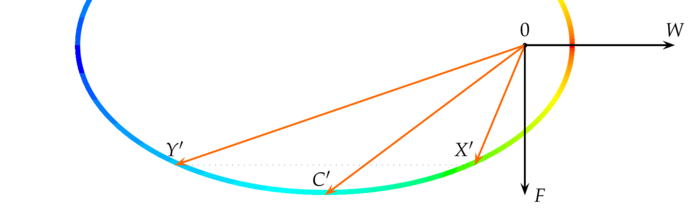
Let $(E,\la.,.\ra)$ be a Lorentz space of dimension $n+1$, i.e. there is a basis $e_0,\ldots,e_n$ for $E$, such that $$ \la e_j,e_k\ra=\e_j\d_{jk} \quad\mbox{where}\quad \e_0=-1 \quad\mbox{and}\quad \forall j\geq1:\e_j=+1 $$ The causal character of a vector $x\in E\sm\{0\}$ depends on the value of $\la x,x\ra$: it is called time-like if $\la x,x\ra < 0$, causal if $\la x,x\ra\leq0$, light-like if $\la x,x\ra=0$ or space-like if $\la x,x\ra > 0$. A non-degenerated subspace $F$ of $E$ must have index $0$ - in which case $(F,\la.,.\ra)$ is Euclidean - or $1$ - in which case $(F,\la.,.\ra)$ is a Lorentz space. In the former case we say $F$ is space-like and in the latter case: $F$ is time-like. If $F$ is neither Euclidean nor a Lorentz space, then $F$ is degenerated and we say $F$ is light-like.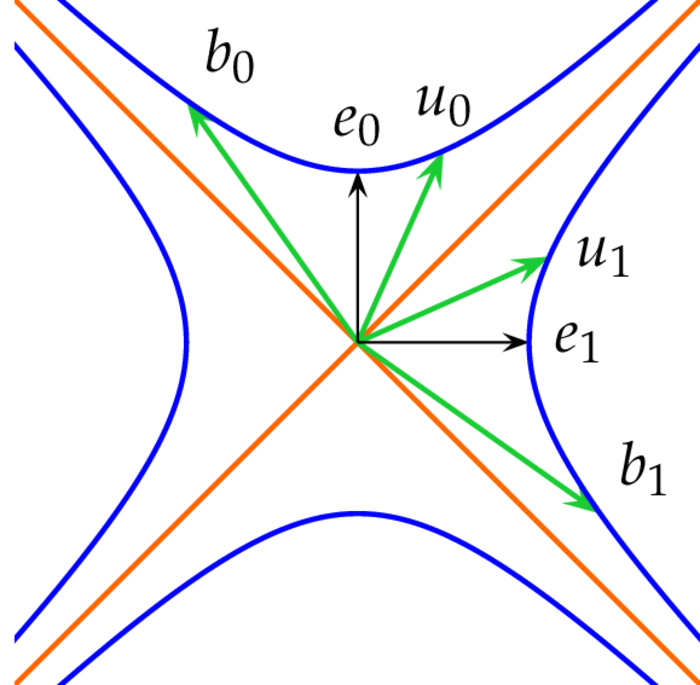
Minkowski space
In the picture above the pairs $b_0,b_1$ and $u_0,u_1$, respectively, form orthonormal bases for $\R_1^2$: $b_0,u_0$ are time-like and $b_1,u_1$ are space-like. Points on the upper or lower arc represent normed time-like vectors and point on the left or right arc are normed space-like vectors - both are also called unit vectors. All four arcs comprise the unit sphere $S_1^1$ of $\R_1^2$. Points on the diagonals represent light-like vectors, which cannot be normalized.
If $b_0,b_1$ is any orthonormal basis for $\R_1^2$ and $x=x_0b_0+x_1b_1$ is any vector, then the vector $y\colon=x_1b_0+x_0b_1$ is orthogonal to $x$. Hence, swapping the components of a vector $x$ produces a vector $y$ orthogonal to $x$.
Let $F$ be a subspace of the Lorentz space $E$. If $\dim F\geq2$ and if $F$ contains a time-like vector $x$, then $F$ contains a space-like vector and a light-like vector.
Let $x$ be time-like, then $x^\perp$ is space-like and $E=\lhull{x}\oplus\lhull{x}^\perp$.
$\proof$ Since $\la.,.\ra$ is trivially non-degenerated on $\lhull{x}$, it follows by lemma that: $E=\lhull{x}\oplus\lhull{x}^\perp$. For all $y\in F^\perp\sm\{0\}$ the vector $y$ is linearly independent from $x$ - because $\lhull{x}$ is non-degenerated - and $\la y,x\ra=0$; now suppose $y$ is causal, i.e. $\la y,y\ra\leq 0$, then: $$ \forall s,t\in\R:\quad \la sy+tx,sy+tx\ra=s^2\la y,y\ra+t^2\la x,x\ra\leq0~. $$ Therefore all non-zero vectors in $\lhull{x,y}$ are causal. On the other hand the two dimensional space $\lhull{x,y}$ must contain a space-like vector. $\eofproof$
Suppose $x,y$ are two causal vectors such that $\la x,y\ra=0$. Then $x,y$ are linearly dependent. Suggested solution.
Let $e_0$ be a time-like vector in the $(n+1)$-dimensional Lorentz space $E$ such that $\la e_0,e_0\ra=-1$. Then there are space-like vectors $e_1,\ldots,e_n\in e_0^\perp$, such that the vectors $e_0,e_1,\ldots,e_n$ form an orthonormal basis for $E$.
The Gram-Schmidt algorithm terminates successfully in a Lorentz space if the first vector is time-like. By rearranging vectors the algorithm works if one of the vectors is time-like.
Suppose $(E,\la.,.\ra)$ is Euclidean and $z\in E$ a unit vector. Then $$ g(x,y)\colon=\la x,y\ra-2\la x,z\ra\la y,z\ra $$ is a Lorentz product on $E$ and $z$ is a time-like unit vector in $(E,g)$. 2. Conversely if $(E,\la.,.\ra)$ is a Lorentz space and $z\in E$ a time-like unit vector, then $$ g(x,y)\colon=\la x,y\ra+2\la x,z\ra\la y,z\ra $$ is a Euclidean product on $E$ and for all $x,y\in E$ we have (suggested solution): $$ |\la x,y\ra|\leq3|x||y| \quad\mbox{where}\quad |x|^2\colon=g(x,x)~. $$
The previous example shows how to define a Euclidean product and thus a metric and a compatible topology on a Lorentz space. Compatibility means that addition and scalar multiplication are continuous operations. Well, all compatible topologies on a finite dimensional vector space are equivalent, but still there are bases of topologies on Lorentz spaces which are somehow better adapted, e.g. the one discussed in exam.
If $z$ is a light-like vector in the Lorentz space $(E,\la.,.\ra)$, then $$ \forall x,y\in E:\quad g(x,y)\colon=\la x,y\ra+\la x,z\ra\la y,z\ra $$ is again a Lorentz product on $E$. Suggested solution.
As for the causal character of a subspace $F$ the following proposition asserts that one may equivalently check the causal character of $F^\perp$:
Let $F$ be a subspace of the Lorentz space $E$, then the following holds:
  1. $F$ is time-like iff $F$ contains a time-like vector.
  2. $F$ is space-like iff $F^\perp$ is time-like.
  3. $F$ is light-like, iff $F^\perp$ is light-like and this holds if and only if $\dim(F\cap F^\perp)=1$.
$\proof$ 1. Obviously we only have to prove that a subspace $F$ of dimension $k$ of the $n$-dimensional Lorentz space $E$ is time-like, if it contains a time-like vector $x$. Since $G\colon=F\cap\lhull{x}^\perp$ is space-like and $F=G\oplus\lhull{x}$, the index of $F$ is $1$, i.e. $F$ is time-like.
2. If $F$ is space-like, then $E=F\oplus F^\perp$ and $F^\perp$ is non-degenerated and thus it's time- or space-like. Suppose $F^\perp$ doesn't contain a time-like vector, then $F^\perp$ is space-like and thus $E=F\oplus F^\perp$ is Euclidean. Conversely if $F^\perp$ is time-like, then it contains a time-like vector $x$ and thus $F\sbe F^{\perp\perp}\sbe x^\perp$ is space-like.
3. $F$ is light-like iff $F$ is degenerated and by lemma this holds if and only if $F^\perp$ is degenerated, which by definition is equivalent to $F^\perp$ is light-like. If $\dim(F\cap F^\perp)=1$, then $F$ is degenerated, i.e. light-like. Conversely if $F$ is degenerated, then $\dim(F\cap F^\perp)\geq1$. If $\dim(F\cap F^\perp)\geq2$, then $F\cap F^\perp$ must contain a space-like vector, which is impossible. $\eofproof$
Suppose $\dim F\geq2$, then $F$ is time-like iff $F$ contains two linearly independent light-like vectors. Suggested solution.
A hyperplane $F$ in $E$ is a subspace of co-dimension one, i.e. $\dim F=\dim E-1$. Thus $F$ is the kernel of a linear functional $x^*\in E^*\sm\{0\}$. Prove that $F$ is space-like iff $x^{*\sharp}$ is time-like; $F$ is light-like iff $x^{*\sharp}\in F$; $F$ is time-like iff $x^{*\sharp}$ is space-like.

Comupational aspects

In general the causal character of a subspace $F$, generated by linearly independent vectors $b_1,\ldots,b_n$ in a Lorentz space $(E,\la.,.\ra)$, can be determined by detecting the index of $\la.,.\ra|_{F\times F}$. By the remarks following the Lagrange-Sylvester Theorem this can in general be done by computing the eigen values of the Gramian $A\colon=(\la b_j,b_k\ra)_{j,k=1}^n$ (cf. e.g. exam). In case of a Lorentz space the determinant of $A$ suffices: $F$ is light-like iff $0$ is an eigen value and this happens if and only if $\det A=0$. $F$ is time-like iff $A$ has exactly one strictly negative eigen value and all the others are strictly positive and this happens if and only if $\det A < 0$. Eventually, $F$ is space-like iff $A$ has only strictly positive eigen values and this happens if and only if $\det A > 0$.
Suppose $F$ is the subspace of $\R_1^4$ generated by $b_1\colon=e_0+2e_3$, $b_2\colon=e_1+2e_2$ and $b_3\colon=e_0-2e_1-e_3$. Determine the causal character of $F$.
The Gramian of the vectors $b_1,b_2$ and $b_3$ is given by the matrix $$ \left(\begin{array}{ccc} 3&0&-3\\ 0&5&-2\\ -3&-2&4 \end{array}\right) $$ and the determinant of this matrix equals $3$. Hence $F$ is space-like.
Suppose $F$ is the subspace of $\R_1^4$ generated by $b_1\colon=e_0+2e_3+e_1$, $b_2\colon=-e_0+e_1+e_2$ and $b_3\colon=-e_0+e_3$. Determine the causal character of $F$.
Suppose $F$ is the subspace of $\R_1^4$ generated by $b_1\colon=e_0-e_1+e_2+e_3$, $b_2\colon=-e_0+e_1-e_2$ and $b_3\colon=e_0+e_2$. Determine the causal character of $F$.
Find vectors $x\in\R_1^4$ in the previous examples such that $F=x^\perp$. Check the causal character of $x$. Suggested solution.
Find necessary and sufficient conditions on the quadratic form $ax^2+2bxy+cy^2$ on $\R^2$ such that the corresponding symmetric bi-linear form defines a Lorentz product on $\R^2$. Suggested solution.
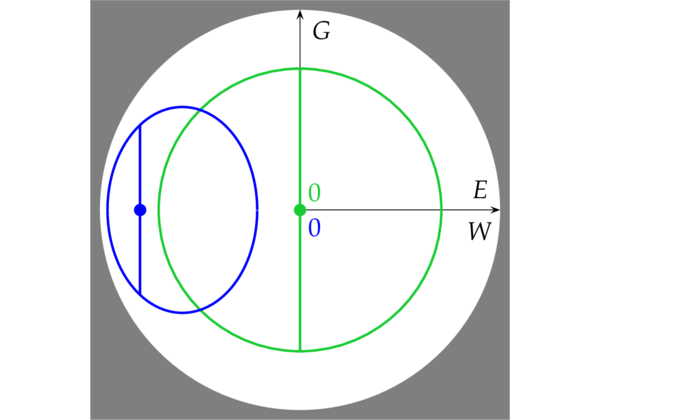
Since the norm $\Vert x\Vert\colon=\sqrt{|\la x,x\ra|}$ on a Lorentz space is not a norm in the usual sense, there is no such notion as 'distance' - the 'distance' of two arbitrary vectors in a Lorentz space is in general not defined; it's only defined for vectors in certain subspaces (cf. section).
If $F$ is a space-like subspace of the Lorentz space $E$, then for all $x,y\in F$: $|\la x,y\ra|\leq\Vert x\Vert\Vert y\Vert$, i.e. the Cauchy-Schwarz inequality holds on $F$ and $\Vert x+y\Vert\leq\Vert x\Vert+\Vert y\Vert$, i.e. $(F,\Vert.\Vert)$ is indeed a normed space and the distance of $x,y\in F$ in $F$ is $\Vert x-y\Vert$.
Both the set of all time-like vectors $Z$ and the set of all space-like vectors are cones but not subspaces. So it may indeed happen that the sum of two space-like or two time-like vectors are of any causal character. Though for an orthonormal basis $b_1,\ldots,b_n$ of a Lorentz space $(E,\la.,.\ra)$ there must be exactly one index $j$ such that $\la b_j,b_j\ra=-1$, an arbitrary basis of a Lorentz space need not contain a time- or space-like vector at all: for example, the basis vectors $e_0-e_1,e_0+e_1$ for $\R_1^2$ are light-like! Finally light-like subspaces of an $n$-dimensional Lorentz space can be of any dimension less than $n$: the vectors $e_0+e_1,e_2,\ldots,e_{n-1}$ generate a light-like $(n-1)$-dimensional subspace of $\R_1^n$.
The space $E$ of all complex hermitian $2\times2$ matrices is the space of all matrices $$ \left( \begin{array}{cc} x& u-iv\\ u+iv&y \end{array}\right) \quad x,u,v,y\in\R~. $$ 1. Verify that $E$ has real dimension four and $A\mapsto-\det(A)$ is a quadratic form on $E$. Thus there is a unique symmetric bi-linear form $g$ on $E\times E$ such that $g(A,A)=-\det(A)$. 2. Show that $g$ is a Lorentz product. 3. The subspace $F\colon=\{A\in E:\tr A=0\}$ is space-like and the identity is a time-like vector and $F$ is orthogonal to the identity. Suggested solution.

Time-Orientation in Lorentz Spaces

Cf. students version

Time cone and light cone

By $Z$ we denote the set of all time-like vectors in $E$, i.e. $$ Z=\{x\in E\sm\{0\}:\la x,x\ra < 0\}~. $$ For $x\in Z$ the set $C(x)\colon=\{y\in Z:\la x,y\ra < 0\}$ is said to be the time cone of $x$. If $y\in Z$ and $x$ is time-like, then $\la x,y\ra\neq0$, for $x^\perp$ is space-like by lemma, and thus we have: $Z=C(x)\cup C(-x)$. The set $$ L\colon=\{x\in E\sm\{0\}:\la x,x\ra=0\} $$ is called the light cone of $E$.
In linear algebra a cone $C$ in a vector-space $E$ is a subset of $E$ such that for all $x\in C$ and all $\l > 0$: $\l x\in C$. Verify that both $Z$ and $L$ are cones and that for all time-like $x\in E$ the set $C(x)$ is a cone.
Suppose $x,y$ are time-like. Then the following holds:
  1. $x$ and $y$ are in the same time cone if and only if $\la x,y\ra < 0$.
  2. $C(x)=C(y)$ iff $\la x,y\ra < 0$.
$\proof$ 1. If $\la x,y\ra < 0$, then $x,y\in C(x)$. So suppose conversely that $x,y\in C(z)$ and $\la z,z\ra=-1$, then: $x=s z+u$ and $y=tz+v$ where $u,v\in z^\perp$; thus $0 > \la x,z\ra=-s$, $0 > \la y,z\ra=-t$ and $$ \la x,x\ra=-s^2+\Vert u\Vert^2,\quad \la y,y\ra=-t^2+\Vert v\Vert^2,\quad \la x,y\ra=-st+\la u,v\ra~. $$ Since $x,y$ are time-like, it follows that $s=|s| > \Vert u\Vert$ and $t=|t| > \Vert v\Vert$ and therefore: $$ \la x,y\ra=-st+\la u,v\ra < -\Vert u\Vert\Vert v\Vert+\la u,v\ra~. $$ Since $u,v$ are space-like, the Cauchy-Schwarz inequality $\la u,v\ra\leq\Vert u\Vert\Vert v\Vert$ implies: $\la x,y\ra < 0$.
2. If $C(x)=C(y)$ then obviously $\la x,y\ra < 0$. Conversely if $\la x,y\ra < 0$, then $x\in C(y)$ and thus for any $z\in C(y)$: $x,z\in C(y)$, which by 1. implies $\la x,z\ra < 0$, i.e. $z\in C(x)$. Hence $C(y)\sbe C(x)$ and exchanging the roles of $x$ and $y$: $C(x)\sbe C(y)$. $\eofproof$
For all time-like vectors $z$ the set $C(z)$ is a convex cone, i.e. for all $x,y\in C(z)$ and all $t\in[0,1]$: $(1-t)x+ty\in C(z)$. $Z$ is not convex! Suggested solution.
Finally we give a geometric interpretation of time-like, space-like and light-like subspaces.
Suppose $F$ is a subspace of the Lorentz space $E$.
  1. $F$ is time-like, iff $F\cap Z\neq\emptyset$.
  2. $F$ is space-like, iff $F\cap Z=F\cap L=\emptyset$.
  3. $F$ is light-like iff $F\cap Z=\emptyset$ and $F\cap L\neq\emptyset$; we say $F$ is tangent to the light-cone.
$\proof$ 1. $F\cap Z\neq\emptyset$ means $F$ contains a time-like vector. 2. $F\cap Z=F\cap L=\emptyset$ means $F$ neither contains a time-like nor a light-like vector, i.e. $F$ is space-like. 3. $F$ is light-like means $F$ is neither time- nor space-like; by 1. and 2. this is equivalent to $F\cap Z=\emptyset$ and $F\cap L\neq\emptyset$.
time cone
$\eofproof$
The following example needs some basic knowledge in topology:
Let $C\colon=C(e)$ be the future time-cone of a Lorentz space $E$. Then the sets $V(x,x^\prime)\colon=(x^\prime-C)\cap(x+C)$, $x,x^\prime\in E$, form a basis of a topology on $E$. Prove that $\pa Z=L\cup\{0\}$. Suggested solution.
Suppose $u\in\Hom(E)$ is a self-adjoint linear operator on a Lorentz space $E$. If $u(L)\sbe Z$, then there is an orthonormal basis $x_j$ and real numbers $\l_j$ such that $u(x_j)=\l_j x_j$. In particular $u$ is diagonalizable. Suggested solution.

Time-orientation and Lorentz transformations

If $x,y$ are time-like, then by lemma: $x\in C(y)$ if and only if $y\in C(x)$ if and only if $C(x)=C(y)$. As $Z=C(x)\cup C(-x)$ there are only two alternatives for time-like vectors $x$ and $y$: $C(x)=C(y)$ or $C(x)=-C(y)$.
By a time-orientation of a Lorentz space $E$ we mean the choice of one of these two cones, i.e. we choose a fixed time-like vector $z$ and declare all vectors in its time cone $C\colon=C(z)$ to be future pointing. For another time-like vector $x$ there are only two alternatives: either $C(x)=C$ or $C(x)=-C$ and this is equivalent to $\la x,z\ra < 0$ or $\la x,z\ra > 0$.
Denote by $e_0,\ldots,e_n$ the canonical basis for $\R_1^{n+1}$, then the vector $e_0$ fixes a time-orientation - below we always consider $\R_1^{n+1}$ with this time-orientation.
The following definition is a slight generalization of a definition given previously(cf. subsection):
Let $(E,\la.,.\ra)$, $(F,\la.,.\ra)$ be a Lorentz spaces and $e_0,\ldots,e_n$ and $f_0,\ldots,f_n$ orthonormal basis for $E$ and $F$ respectively such that $\la e_0,e_0\ra=\la f_0,f_0\ra=-1$. An isomorphism $u:E\rar F$ is called a linear isometry, if $$ \forall x,y\in E:\quad\la u(x),u(y)\ra=\la x,y\ra~. $$
The bases $e_0,\ldots,e_n$ and $f_0,\ldots,f_n$ define orientations on $E$ and $F$, respectively, and the associated volume forms are given by $\vol E(e_0,\ldots,e_n)=\vol F(f_0,\ldots,f_n)=+1$, i.e. (cf. subsection): \begin{eqnarray*} \vol E(x_0,\ldots,x_n)&=&\det(e_j^*(x_k))=\det(\e_j\la e_j,x_k\ra),\quad \e_j\colon=\la e_j,e_j\ra\\ \vol F(y_0,\ldots,y_n)&=&\det(f_j^*(y_k))=\det(\d_j\la f_j,y_k\ra),\quad \d_j\colon=\la f_j,f_j\ra~. \end{eqnarray*} A linear isometry $u:E\rar F$ is orientation preserving, if the orthonormal basis $u(e_0),\ldots,u(e_n)$ has the same orientation as the given orthonormal basis $f_0,\ldots,f_n$. By exam this comes down to saying that the determinant of the matrix representation of $u$ with respect to the bases $e_0,\ldots,e_n$ and $f_0,\ldots,f_n$ equals $+1$. A linear isometry maps time-like, space-like and light-like vectors to time-like, space-like and light-like vectors, but even an orientation preserving linear isometry doesn't necessarily map future pointing vectors to future pointing vectors. Thus we come up with the following definition:
An orientation preserving linear isometry $u:E\rar F$ is called a Lorentz transformation, if $u(e_0)\in C(f_0)$.
This definition implies that a Lorentz transformation not only maps time-, space- and light-like vectors to time-, space- and light-like vectors - that's what isometries do, it also maps a future pointing vector to a future pointing vector. Indeed, suppose $u(e_0)\in C(f_0)$, then $f_0\in C(u(e_0))$; now if $x\in C(e_0)$, then $\la x,e_0\ra < 0$ and since $u$ is an isometry: $u(x)\in C(u(e_0))$, i.e. $u(x)$ and $f_0$ are in the same time cone, which by lemma means: $\la u(x),f_0\ra < 0$ and thus $u(x)\in C(f_0)$.
How to characterize a Lorentz transformation by means of its matrix? Let $u:E\rar E$ be a linear map and $A=(a_{jk})_{j,k=0}^n$ the matrix representation of $u$ with respect to the orthonormal basis $e_0,\ldots,e_n$ for $E$ such that $e_0$ defines the time orientation. $u$ is an isometry if and only if $u^*u=1$; for the matrix $A$ this means (cf. subsection) $$ DA^tD=A^{-1}, $$ where $D=diag\{-1,1,\ldots,1\}$: the matrix $A^{-1}$ can thus be obtained by transposing $A$, then multiplying the first row by $-1$ and finally multiplying the first column by $-1$. From this (or lemma) it follows that the determinant of an isometry is either $+1$ or $-1$. Finally $u$ preserves the time orientation iff $\la u(e_0),e_0\ra < 0$, which holds if and only if $$ a_{00} \colon=e_0^*(u(e_0)) =\la e_0^{*\sharp},u(e_0)\ra =\la-e_0,u(e_0)\ra > 0~. $$ Summarizing a homomorphism $u\in\Hom(E)$ is a Lorentz transformation if and only if the following three conditions are met:
  1. $u$ is an isometry, which holds if and only if $DA^tD=A^{-1}$.
  2. $u$ is orientation preserving, which holds if and only if $\det A=+1$.
  3. $u$ preserves the time orientation, which holds if and only if $a_{00} > 0$.

Lorentz transformations and skew-symmetric transformations

1. Suppose $f,g:\R\rar E$ are smooth curves in an inner product space $(E,\la.,.\ra)$ (of finite dimension). Then the derivative of $s\mapsto\la f(s),g(s)\ra$ is given by $\la f^\prime(s),g(s)\ra+\la f(s),g^\prime(s)\ra$. 2. For all $x\in E$ and all $u\in\Hom(E)$ the derivative of $f(s)\colon=e^{su}x$ is given by $ue^{su}x$.
If $u\in\Hom(E)$ is skew-symmetric, then $e^u$ is a Lorentz transformation.
$\proof$ 1. Consider for any pair $x,y\in E$ the function $f:\R\rar\R$, $f(s)\colon=\la e^{su}x,e^{su}y\ra$. Then $f(0)=\la x,y\ra$ and $f^\prime(s)=\la ue^{su}x,e^{su}y\ra+\la e^{su}x,ue^{su}y\ra$; since $u^*=-u$ it follows that $f^\prime(s)=0$, i.e. $f$ is constant. Hence $e^{su}$ is for all $s\in\R$ an isometry. 2. Since $g:s\mapsto\det(e^{su})$ is continuous, $g(s)=\pm1$ and $g(0)=1$, we must have $g(s)=1$. 3. We need to verify that $e^uz\in C(z)$ for some time-like vector $z$ defining the time-orientation. So look at the function $s\mapsto\la e^{su}z,z\ra$. Both $z$ and $e^{su}z$ are time-like and by the wrong Cauchy-Schwarz inequality (cf. proposition): $|\la e^{su}z,z\ra|\geq1$; since $\la z,z\ra=-1$, we conclude by continuity: $\la e^{su}z,z\ra\leq-1$, i.e. $e^uz\in C(z)$. $\eofproof$
If $(E,\la.,.\ra)$ is any inner product space and $u\in\Hom(E)$ is skew-symmetric, then $e^u$ is an orientation preserving isometry.
Suppose $u:\R_1^2\rar\R_1^2$ is a Lorentz transformation; let $A$ be the matrix representation of $u$ with respect to the canonical basis $e_0,e_1$ for $\R_1^2$. Prove that there is a unique number $\vp\in\R$ such that $$ A =\left(\begin{array}{cc} \cosh(\vp)&\sinh(\vp)\\ \sinh(\vp)&\cosh(\vp) \end{array}\right) =\exp\left(\begin{array}{cc} 0&\vp\\ \vp&0 \end{array}\right)~. $$
Since $e_0,e_1$ is an orthonormal basis, the matrix of a linear isometry must be of the form $$ \left(\begin{array}{cc} a&\e b\\ b&\e a \end{array}\right) $$ for $a,b\in\R$, $-a^2+b^2=-1$ and $\e=\pm1$. The determinant of this matrix is $\e(a^2-b^2)=\e$. Thus $u$ is a Lorentz transformation iff $a^2-b^2=1$, $\e=1$ and $a > 0$. This is the case if and only if there is a unique number $\vp\in\R$ such that $a=\cosh\vp$, $b=\sinh\vp$ and $\e=1$. Here is a simple picture: the above Lorentz transformation maps the positive orthonormal basis $b_0,b_1$ onto another positive orthonormal basis $u(b_0),u(b_1)$.
lorentz transform
The matrix of the inverse $u^{-1}$ is given by $$ \exp\left(\begin{array}{cc} 0&-\vp\\ -\vp&0 \end{array}\right) =\left(\begin{array}{cc} \cosh(\vp)&-\sinh(\vp)\\ -\sinh(\vp)&\cosh(\vp) \end{array}\right)~. $$ The following example gives another description of Lorentz transformations in $\R_1^2$, which may look more familiar:
Suppose $u:\R_1^2\rar\R_1^2$ is a Lorentz transformation; let $A$ be the matrix representation of $u$ with respect to the canonical basis $e_0,e_1$ for $\R_1^2$. Prove that there is a unique number $v\in(-1,1)$ such that $$ A =\frac1{\sqrt{1-v^2}}\left(\begin{array}{cc} 1&v\\ v&1 \end{array}\right)~. $$ In coordinates: $u$ maps the point with coordinates $(x_0,x_1)$ to the point with coordinates $$ \Big(\frac{x_0+vx_1}{\sqrt{1-v^2}},\frac{vx_0+x_1}{\sqrt{1-v^2}}\Big)~. $$
Remark: In classical mechanics a uniform motion with speed $v$ in the direction $b_1$ is a linear map $u:\R\times E\rar\R\times E$, $(t,x)\mapsto(t,x+vb_1t)$, where $E$ is a Euclidean space - this is a particular Galilean transformation. In case $E=\R$ the uniform motion with speed $v$ is given by $(t,x)\mapsto(t,tv+x)$ and the Lorentz transformation given in exam is the relativistic counterpart thereof.
Suppose $u:\R_1^2\rar\R_1^2$ is linear and let $(a_{jk})$ be the matrix representation of $u$ with respect to the canonical basis $e_0,e_1$ for $\R_1^2$. Prove that $u$ is skew-symmetric iff $a_{11}=a_{22}=0$ and $a_{21}=a_{12}$. Compute the eigen values and eigen vectors of any skew-symmetric $u:\R_1^2\rar\R_1^2$.

Boosts and rotations

A Lorentz transformation $u$ on a Lorentz space $E$ is called a boost if there is some orthonormal basis $b_0,\ldots,b_n$, such that $b_0$ is time-like and future pointing and \begin{eqnarray*} u(b_0)&=&\cosh(\vp)\,b_0+\sinh(\vp)\,b_1\\ u(b_1)&=&\sinh(\vp)\,b_0+\cosh(\vp)\,b_1\\ u(b_j)&=&b_j \quad\mbox{for all $j\geq 2$}~. \end{eqnarray*} $b_1$ is called the direction of the boost and $|\tanh(\vp)|$ the speed of the boost.
Verify that the boost above is given by $u=e^v$ where $$ v(b_0)=\vp b_1,\quad v(b_1)=\vp b_0,\quad v(b_j)=0 \quad\mbox{for all $j\geq 2$.} $$
A boost $u$ is always diagonalizable and it has exactly two light-like eigen vectors: $b_0+b_1$ and $b_0-b_1$ and $\dim E-2$ space-like eigen vectors. Conversely, if a Lorentz transformation is diagonalizable with two light-like eigen vectors $e_0$ and $e_1$ (with eigen values $\l$ and $1/\l$) and $\dim E-2$ space-like eigen vectors (with eigen value $1$) orthogonal to $\lhull{e_0,e_1}$, then $u$ is a boost (in the direction $e_0+e_1$ or $e_0-e_1$, depending on the causal character) and $\cosh\vp=(\l+1/\l)/2$.
A Lorentz transformation $u$ that fixes some time-like vector $z$ is called a rotation because $u|z^\perp$ is an orientation preserving linear isometry of the Euclidean space $z^\perp$.
In a two dimensional Lorentz space there is only one rotation: the identity.
The following shows that every Lorentz transformation is the composition of a rotation (about a fixed time-like vector) and a boost: Suppose $u\in\Hom(E)$ is a Lorentz transformation mapping the unit time-like vector $z$ into its time cone $C(z)$. Then $$ u(z)=\cosh(\vp)z+\sinh(\vp)b_1, $$ where $b_1\perp z$ and $\Vert b_1\Vert=1$. Put \begin{eqnarray*} v(z)&=&\cosh(\vp)z-\sinh(\vp)b_1\\ v(b_1)&=&-\sinh(\vp)z+\cosh(\vp)b_1\\ \mbox{and}&&v|\lhull{z,b_1}^\perp=id~. \end{eqnarray*} Then $v$ is a boost in the direction $b_1$ and $vu(z)=z$. Hence $vu$ is a rotation $r$ about $z$ and $u=v^{-1}r$.
Once we know that a Lorentz transformation $u\in\Hom(E)$ is a boost, we can determine $\vp$ quite easily: $\tr u=2(\cosh\vp-1)+\dim E$.
Describe all Lorentz transformations in $\R_1^3$. Suggested solution.
The following example is the analogue of the vector product in the Euclidean space $\R^3$ for the Lorentz space $\R_1^3$:
There is a unique bi-linear map $\R_1^3\times\R_1^3\rar\R_1^3$, $(x,y)\mapsto x*y$ with the following properties:
  1. For all $x,y\in\R_1^3$: $y*x=-x*y$.
  2. $e_0*e_1=e_2$, $e_1*e_2=-e_0$, $e_2*e_0=e_1$.
1. Verify that for all $x,y\in\R_1^3$: $\la x,x*y\ra=\la y,x*y\ra=0$. Thus given any pair of vectors $(x,y)$ the vector $x*y$ is orthogonal to both $x$ and $y$. 2. For all $x\in\R_1^3$ the linear map $y\mapsto x*y$ is skew-symmetric on $\R_1^3$. It follows that $\o:(x,y,z)\mapsto\la x*y,z\ra$ is a volume-form on $\R_1^3$; show that $\o(e_0,e_1,e_2)=+1$ and thus by lemma: $\o(x_0,x_1,x_2)=\det(e_j^*(x_k))$. 3. Verify Jacobi's identity: for all $x,y,z$: $x*(y*z)+y*(z*x)+z*(x*y)=0$. Suggested solution.
This construction generalizes to an alternating $(n-1)$-form $\O$ on $\R_\nu^n$ with values in $\R_\nu^n$, which has the property that given any $(n-1)$-tuple of vectors $x_1,\ldots,x_{n-1}\in\R_\nu^n$ the vector $\O(x_1,\ldots,x_{n-1})$ is orthogonal to all vectors $x_1,\ldots,x_{n-1}$. An even more general procedure is provided by the so called Hodge $*$-operator, cf. section in a subsequent chapter.
Find a vector orthogonal to the vectors $2e_0+e_1+e_2$ and $e_0+e_1+e_2$ in $\R_1^3$ and show that the matrix $$ \left(\begin{array}{ccc} \sqrt2&1&0\\ 1/\sqrt2&1&-1/\sqrt2\\ 1/\sqrt2&1&1/\sqrt2 \end{array}\right) $$ defines a Lorentz transformation in $\R_1^3$. Is it diagonalizable? Is it a boost, a rotation? Finally compute the inverse matrix on your own! Suggested solution.
Let $(E,g)$ be the space described in exam. 1. For all $X\in\Sl(2,\C)$ the linear map $A\mapsto XAX^*$ is an isometry of the Lorentz space $(E,g)$. 2. The map $\Phi:X\mapsto(A\mapsto XAX^*)$ from $\Sl(2,\C)$ into the group $G$ of isometries of $(E,g)$ is a homomorphism, i.e. $\Phi(XY)=\Phi(X)\Phi(Y)$. 3. For $X\in\SU(2)$ $\Phi(X)$ has a time-like eigenvector with eigenvalue $1$ and thus $\Phi(X)$ is a rotation. 4. For $X$ positive $\Phi(X)$ is a boost. Suggested solution.
$\Phi:\Sl(2,\C)\rar G$ is a surjectiv homomorphism with kernel $\pm1$ onto the group $G$ of Lorentz transformations on $(E,g)$ (cf. exam). Hence the group of Lorentz transformations on $\R_1^4$ is isomorphic to $\Sl(2,\C)/\{\pm1\}$. Suggested solution

Geometry on the time cone

The following result indicates that the world of time-like vectors is somehow Euclidean but turned upside down.
  1. Let $x,y$ be time-like, then the wrong Cauchy-Schwarz inequality: $|\la x,y\ra|\geq\Vert x\Vert\Vert y\Vert$ holds with equality if and only if $y=\l x$.
  2. If $x$ and $y$ are time-like and future pointing, then there is exactly one number $\vp\geq0$, such that $\la x,y\ra=-\Vert x\Vert\Vert y\Vert\cosh(\vp)$. Moreover $\Vert x+y\Vert\geq\Vert x\Vert+\Vert y\Vert$ and $$ \Vert y-x\Vert^2 =\Big|\Vert x\Vert^2+\Vert y\Vert^2-2\Vert x\Vert\Vert y\Vert\cosh(\vp)\Big|~. $$
Remember, for time-like vectors $x$ we have $\Vert x\Vert\colon=\sqrt{-\la x,x\ra}$.
$\proof$ 1. Since $y=tx+u$ where $u\in x^\perp$, we have: $\la u,u\ra\geq0$ and $\la y,y\ra=t^2\la x,x\ra+\la u,u\ra$, thus $t^2\Vert x\Vert^2=\Vert y\Vert^2+\la u,u\ra$ and therefore $$ \la x,y\ra^2 =t^2\la x,x\ra^2 =t^2\Vert x\Vert^4 =(\Vert y\Vert^2+\la u,u\ra)\Vert x\Vert^2\\ \geq\Vert y\Vert^2\Vert x\Vert^2~. $$ Equality holds iff $u=0$, i.e. $y=tx$.
2. $x$ and $y$ are in the same time cone, thus $\la x,y\ra < 0$ and the first claim is obvious by 1. As for the second we notice that $\la x+y,x+y\ra=\la x,x\ra+\la y,y\ra+2\la x,y\ra$ and since all terms are negative; we conclude by 1. that $$ \Vert x+y\Vert^2 =\Vert x\Vert^2+\Vert y\Vert^2-2\la x,y\ra \geq\Vert x\Vert^2+\Vert y\Vert^2+2\Vert x\Vert\Vert y\Vert =(\Vert x\Vert+\Vert y\Vert)^2~. $$ Since $\la x,y\ra=-\Vert x\Vert\Vert y\Vert\cosh(\vp)$ for some $\vp\geq0$, we eventually get $$ \la y-x,y-x\ra=\la x,x\ra+\la y,y\ra+2\Vert x\Vert\Vert y\Vert\cosh(\vp) $$ and the last assertion follows. $\eofproof$
If $x,y$ are time-like and linearly independent, then the vector $x+ty$ is light-like for exactly two values of $t\in\R$. Suggested solution.
As in the Euclidean case the number $\vp$ in proposition has a geometric interpretation: Suppose $x$ and $y$ are future pointing time-like unit vectors, then $\vp$ is the Lorentz-length (cf. exam) of part of the arc $$ \lhull{x,y}\cap S(E)\cap C(z) =\{u=\a x+\b y:\,\la u,u\ra=-1,\la u,z\ra < 0,\a,\b\in\R\} $$ joining $x$ and $y$; the inner product of $x$ and $y$ is $-\cosh(\vp)$. The picture below visualizes the case $E=\R_1^2$ and $z=e_0$:
time cone
In the Euclidean case $\vp$ is the Euclidean-length of the arc $\lhull{x,y}\cap S(E)$ joining the unit vectors $x$ and $y$ and the inner product of $x$ and $y$ is $\cos(\vp)$. Hence in Euclidean spaces the analogue to the last formula in proposition is the relation $$ \norm{x-y}^2=\Vert x\Vert^2+\Vert x\Vert^2-2\Vert x\Vert\Vert y\Vert\cos\vp~. $$ where $\vp$ is the angle of the vectors $x$ and $y$. This is known as the 'cosine rule'.

Instantaneous Observers

In this section we will explore the key concepts that connect theoretical physics to Lorentz spaces. Throughout the following section we will use capital letters $X,Y,Z,\ldots$ for vectors! Cf. students version in german

Local time axis and rest space

In physics the speed of light is a universal constant and material particles are associated some quantity called rest mass.

Here and in almost all what is going to follow we assume that the speed of light is 1 and all instantaneous observers have rest mass 1!

In relativity any future pointing light-like vector $X$ of a time oriented Lorentz space $E$ is called a light-like particle (actually it should be called an instantaneous light-like particle) or a photon and any future pointing time-like vector $Z$ satisfying \begin{equation}\label{iobeq1}\tag{IOB1} \la Z,Z\ra=-1 \end{equation} is called an instantaneous observer or an (instantaneous) material particle. The one dimensional subspace $\lhull{Z}$ generated by $Z$ is called the local time axis and the subspace $Z^\perp$ orthogonal to $Z$ is called the local rest space of $Z$. Light-like particles neither have a local time axis nor a rest space. By lemma $Z^\perp$ is a Euclidean subspace of the Lorentz space $E$ and it's the relativistic counterpart of the 'space of perception' in our Newtonian view. It's the space of perception for $Z$. But in contrast to our Newtonian view the rest space differs from observer to observer. Consequently, when comparing observations of two different instantaneous observer we need some transformation from the rest space of the first onto the rest space of the second - we will choose a boost, which maps the first instantaneous observer onto the second and which is the identity on the intersection of the two rest spaces. This way we may identify the two rest spaces, but this identification is in no way cannonical!
Beware! in both cases (material or light-like) the vector $Z$ only represents the particle at one and only one event - thus the term 'instantaneous'. The vector $Z$ is not a model for the trajectories of the particle. Its classical counterpart would rather be the velocity of the particle at a particular point. But in contrast to classical physics the vector $Z$, which is the relevant part in relativity, is not directly observable: only its energy and its momentum are observable for another instantaneous observer. Also, there is no immediate transfer of data between instantaneous observers at different events. By way of precaution assume that perceptions at different events are incomparable!

Energy, momentum and velocity

To start with we present two essential notions: energy and momentum with respect to an instantaneous observer $Z$. Suppose $X$ is another instantaneous observer, i.e. $\la X,X\ra=-1$ or light-like, i.e. $\la X,X\ra=0$, then \begin{equation}\label{iobeq2}\tag{IOB2} \b\colon=-\la Z,X\ra \end{equation} is called the energy of $X$ with respect to the instantaneous observer $Z$. The orthogonal projection (in the Lorentz space $E$) \begin{equation}\label{iobeq3}\tag{IOB3} P\colon=X+\la Z,X\ra Z=X-\b Z \end{equation} of $X$ to the local rest space of $Z$ is called the momentum of $X$ for the instantaneous observer $Z$, i.e. we have the orthogonal decomposition $X=-\la Z,X\ra Z+P$: the energy is just the component of $X$ along the local time axis of $Z$ - its time component - and the momentum is the orthogonal projection of $X$ on the rest space of $Z$ - its spatial component. Finally the vector \begin{equation}\label{iobeq4}\tag{IOB4} V\colon=\frac{P}{-\la Z,X\ra}=\frac{P}{\b} \end{equation} is called the velocity of $X$ with respect to the instantaneous observer $Z$. Similar to the classical definition velocity is 'spatial component' divided by 'time component' - because $P$ is the orthogonal projection of $X$ to the rest space of $Z$ and $-\la Z,X\ra$ is the component of $X$ along the time axis of $Z$. Geometrically momentum and velocity indicate the direction of motion of $X$ for the instantaneous observer $Z$. The concept of e.g. a material particle (instantaneous observer) thus comprises both the concept of energy and the concept of momentum, but the latter two are just components relative to the time axis and the rest space of another instantaneous observer.
Let $Z$ be an instantaneous observer. The energy of $Z$ with respect to another instantaneous observer $X$ is always greater or equal to $1$ and the equation $\la Z,Z\ra=-1$ means that the energy of $Z$ with respect to itself - also called rest energy - equals $1$. Obviously the momentum and the velocity of $Z$ with respect to itself vanish.
A few immediate conclusions can be drawn from these definitions:
  1. Energy, momentum and velocity of any material or light-like particle are only defined with respect to an instantaneous observer!
  2. Symmetry of energy: the energy of an instantaneous observer $X$ with respect to an instantaneous observer $Z$ coincides with the energy of the instantaneous observer $Z$ with respect to the instantaneous observer $X$.
  3. If $P$ is the momentum of $X$ for $Z$ and $Q$ the momentum of $Z$ for $X$, then $$ \la P,P\ra =\la X,X\ra+\la Z,X\ra^2 =-1+\la Z,X\ra^2 =\la Z,Z\ra+\la Z,X\ra^2 =\la Q,Q\ra $$ i.e. the norm of $P$ equals the norm of $Q$. But unlike the classical relation, we do not have $Q=-P$, for $$ P+Q=(Z+X)(1+\la Z,X\ra) $$ and since $Z,X$ are future pointing this vanishes if and only if $\la Z,X\ra=-1$. By the wrong Cauchy-Schwarz inequality this occurs if and only if $Z=X$.
So far we just gave a couple of definitions. Now it's time to verify that our model exactly renders two facts: the speed, i.e. the norm of the velocity of an instantaneous observer $X$ with respect to another instantaneous observer $Z$ is stricly less than 1: Suppose $P$ is the momentum of $X$ with respect to $Z$, then $$ P=X+\la Z,X\ra Z $$ and since $\la X,X\ra=\la Z,Z\ra=-1$: $\la P,P\ra=-1+\la X,Z\ra^2$; therefore the speed is given by: $$ \Vert V\Vert^2 =\la V,V\ra =\frac{\la P,P\ra}{\la Z,X\ra^2} =\frac{-1+\la Z,X\ra^2}{\la Z,X\ra^2} < 1~. $$ The second fact: The speed of light with respect to any instantaneous observer is $1$. Suppose $X$ is light-like and $V$ is the velocity of $X$ with respect to an instantaneous observer $Z$. The momentum $P$ of $X$ with respect to $Z$ is again given by: $$ P=X+\la Z,X\ra Z $$ and since $\la X,X\ra=0$: $\la P,P\ra=\la Z,X\ra^2$ and thus we get for the velocity $V$ of $X$ with respect to $Z$: $$ \la V,V\ra=\frac{\la P,P\ra}{\la Z,X\ra^2}=\frac{\la Z,X\ra^2}{\la Z,X\ra^2} = 1~. $$
Energy $\b$ and norm of the momentum $P$ of an instantaneous observer or a light-like particle $X$ (with respect to $Z$) are therefore related by \begin{eqnarray*} \b^2=1+\Vert P\Vert^2&&\quad\mbox{if $X$ is an instantaneous observer}\\ \b=\Vert P\Vert&&\quad\mbox{if $X$ is light-like} \end{eqnarray*} Thus in case $X$ is light-like the norm or length of $P$ is the energy of $X$ (with respect to $Z$) and in case $X$ is material its squared energy is its squared rest energy plus the square of the norm of its momentum - that's the relativistiv energy-momentum relation; in SI-units: $E^2=(mc^2)^2+c^2\Vert P\Vert^2$ for material particles and $E=c\Vert P\Vert$ for photons.
Let $Z$ be an instantaneous observer, $a\in\R$, $E\perp Z$ a unit vector, $X\colon=\cosh(a)Z+\sinh(a)E$ and $Y\colon=Z-E$. Verify that $X$ is an instantaneous observer and $Y$ is light-like. Calculate the energy and the momentum of $Y$ with respect to $X$.
Let $X=\cosh(a)Z+\sinh(a)E$ and $Y\colon=\cosh(b)Z+\sinh(b)E$. Then energy, momentum, velocity and speed of $Y$ with respect to $X$ are given by $$ \cosh(b-a),\quad \sinh(b-a)F,\quad \tanh(b-a)F,\quad |\tanh(b-a)| $$ where $F\colon=\sinh(a)Z+\cosh(a)E$ is a unit vector orthogonal to $X$.

Reconstructing instantaneous observers from energy and momentum/velocity

So far we know how to decompose a material or light-like particle into its energy and its momentum (with respect to a given instantaneous observer $Z$). Thus $Z$ can determine the energy and the momentum of another instantaneous observer $X$ or a light-like particle $X$, i.e. a photon, all of course at the same event in spacetime. The energy is just a real number but momentum and velocity are vectors in the rest space of $Z$. But neither energy nor momentum constitute relevant quantities in relativity, primarily because they depend on $Z$. Both are incorporated into the vector $X$, akin to the components of a vector in classical mechanics. What really matters in theory of relativity is the vector $X$, which does not depend on any other observer. Thus the instantaneous observer $Z$ can determine the energy $\b$ of another instantaneous observer $X$ and its velocity (or momentum) and both depend on $Z$.
1. Can we recover from this data - energy and momentum - the vector $X$? Of course this can be done because energy and momentum simply correspond to an orthogonal decomposition. To see how to accomplished this let $E$ be a unit vector in the rest space $Z^\perp$ of $Z$ such that the velocity (of $X$ with respect to $Z$) is given by $vE$ for some $v\in(0,1)$ - thus $v$ is the speed of $X$ with respect to $Z$. The energy $\b$ is by definition $\b\colon=-\la X,Z\ra$ and the momentum $P$ is $P\colon=v\b E$; again by definition we have $$ v\b E=P\colon=X+\la X,Z\ra Z=X-\b Z $$ and therefore: \begin{equation}\label{iobeq5}\tag{IOB5} X=\b(Z+vE)~. \end{equation} From $\la X,X\ra=-1$ we infer that: $-1=\b^2(-1+v^2)$. Thus we get the familiar relations for the energy $\b$ and the momentum $P$: $$ \b =-\la X,Z\ra =\frac1{\sqrt{1-v^2}} \quad\mbox{and}\quad P=\frac{vE}{\sqrt{1-v^2}}~. $$
Determine the momentum $Q$ of $Z$ with respect to $X$ in terms of $P$ and $X$.
2. Can this also be done in case $X$ is light-like? Of course, this is even simpler; if you know the energy $\b\colon=-\la X,Z\ra$ and the momentum $P\colon=X+\la X,Z\ra Z$ of the light-like $X$, then obviously: $X=\b Z+P$. Thus if $E$ is a unit vector in $Z^\perp$, then \begin{equation}\label{iobeq6}\tag{IOB6} X=\b(Z+E) \end{equation} is light-like with energy $\b$, momentum $P=\b E$ and velocity $E$ with respect to $Z$.
Let $Z,X,Y$ be instantaneous observers, such that $X=\b(Z+uE)$, $Y=\g(X+vF)$, where $E\perp Z$ and $F\perp X$ are unit vectors. Determine the energy $e$ and the momentum $P$ of $Y$ with respect to $Z$ in terms of $Z$, $E$ and $F$. Suggested solution.

Energy and momentum/velocity under Lorentz transformations

If $u\in\Hom(E)$ is a Lorentz transformation, then for any instantaneous observer $T$ we get another instantaneous observer $u(T)$ and the local rest space of $u(T)$ is just the image of the local rest space of $T$ under $u$: indeed, from exam and the fact that $u$ is an isometry we infer that $$ u(T)^\perp=(u^*)^{-1}(T^\perp)=u(T^\perp)~. $$ Moreover, by definition of a Lorentz transformation, if $Y$ is causal, i.e. another instantaneous observer or a light-like particle, then the energy and the momentum of $u(Y)$ with respect to $u(T)$ is the energy of $Y$ and the image under $u$ of the momentum $P\colon=Y+\la Y,T\ra T$ of $Y$ with respect to $T$: $$ u(Y)+\la u(Y),u(T)\ra u(T) =u(Y)+\la Y,T\ra u(T) =u(Y+\la Y,T\ra T) =u(P)~. $$ Conversely, given two instantaneous observers $Z$ and $T$ we can find a boost $u$ mapping $T$ to $Z$ and the direction of the boost is the direction $Z$ moves to for $T$.
Let $Z,T$ be instantaneous observers; $Z$ moves with respect to $T$ in direction $E$ with speed $v$. Suppose $u:\lhull{T,E}\rar\lhull{T,E}$ is a Lorentz transformation (actually it's a boost) such that $u(T)=Z$. Then $T$ moves with respect to $Z$ in direction $-u(E)$ with speed $v$.
1. $\pm u(E)$ are the only unit vectors in $\lhull{T,E}$ orthogonal to $Z$.
2. We simply have to verify that $T=\b(Z-vu(E))$, i.e. $$ u^{-1}(T)=\b(T-vE)~. $$ The matrices of $u$ and $u^{-1}$ with respect to the basis $T,E$ are $$ \b\left(\begin{array}{cc} 1&v\\ v&1 \end{array}\right) \quad\mbox{and}\quad \b\left(\begin{array}{cc} 1&-v\\-v&1 \end{array}\right)~. $$ In particular $u^{-1}(T)=\b(T-vE)$.

The classical limit $v\to 0$

If $\Vert V\Vert\ll1$, then $\b\sim1+\Vert V\Vert^2/2$ (up to terms of order $\Vert V\Vert^4$) and thus $\b$ essentially coincides with the sum of the rest energy, which is $1$, and the classical kinetic energy $\Vert V\Vert^2/2$. Moreover for an instantaneous observer $X=\b(Z+V)$ the orthogonal projection of $Y$ on its rest space $X^\perp$ is (up to order $\Vert V\Vert$) the orthogonal projection of $Y$ on the rest space $Z^\perp$ of $Z$! For instance the momentum of $X$ with respect to $Z$ is $\b V\sim V$ (up to terms of order $\Vert V\Vert^2$) and the momentum of $Z$ with respect to $X$ $$ Z+\la Z,X\ra X =Z-\b\b(Z+V) \sim-V~. $$ Thus in the limit $\Vert V\Vert\to0$ we recover the classical description.

Doppler's principle

Let $Z$ be an instantaneous observer and $E,F\in Z^\perp$ normed vectors. Then $$ Y\colon=\g(Z+F) $$ is light-like in the direction of $F$ (for $Z$) and its energy equals $\g$. Suppose $X$ is another instantaneous observer with velocity $vE$, $v\in(-1,1)$ with respect to $Z$, i.e. $$ X=\b(Z+vE) $$ and the energy of $Y$ with respect to $X$ is $$ -\la Y,X\ra=\g\b(1-v\la E,F\ra)~. $$ Let's see what can be said in case $X$ and $Y$ move in the same direction (with respect to $Z$), i.e. if $F=E$: Since $\b=1/\sqrt{1-v^2}$, we get: $$ -\la Y,X\ra=\g\sqrt{\frac{1-v}{1+v}}~. $$ Thus if $v > 0$, $X$ observes a lower energy, a red shift of light; if $v < 0$ i.e. $X$ moves towards the source of light, $X$ observes a blue shift of light.
What can be said in the transversal case, when $X$ moves orthogonally to $Y$ for $Z$, i.e. $F\perp E$? In this case the energy of $Y$ with respect to $X$ is $$ -\la Y,X\ra=\g\frac1{\sqrt{1-v^2}}, $$ which is greater than the energy $\g$ of $Y$ with respect to $Z$. $X$ experiences a blue shift, which the standard classical model doesn't explain; it's a new phenomenon predicted by the relativitstic model. All these sorts of phenomena are called: Doppler effect. One of the applications is the so-called laser surface velocimeter measuring velocities of moving surfaces.

Conservation of energy-momentum

This conservation doesn't make sense without the notion of rest mass: Suppose $m > 0$ and $Z$ is an instantaneous observer, then $mZ$ is called an instantaneous observer of rest mass $m$ or a material particle of rest mass $m$. If $m_1Z_1$ and $m_2Z_2$ collide and form a material particle $MZ$ - that's what physicists call a totally inelastic collision, then in relativity the following relation is postulated: \begin{equation}\label{iobeq7}\tag{IOB7} m_1Z_1+m_2Z_2=MZ \end{equation} That's called conservation of energy-momentum (because the vectors $Z_1,Z_2,Z$ are somehow composed of these two parts). Assuming $Z,Z_1$ and $Z_2$ to be material, we get $$ -M^2 =\la MZ,MZ\ra =-m_1^2-m_2^2+2m_1m_2\la Z_1,Z_2\ra $$ and since the energy $\b\colon=-\la Z_1,Z_2\ra$ is greater than $1$ we conclude that: $$ M^2=m_1^2+m_2^2+2\b m_1m_2\geq(m_1+m_2)^2~. $$ In case $Z_2$ is light-like with energy $\g$ we have instead of \eqref{iobeq7}: $m_1Z_1+\g Z_2=MZ$ and therefore $$ M^2=m_1^2+2\b\g m_1\geq m_1^2~. $$
Suppose $mZ_1=m(\cosh\vp\,T+\sinh\vp\,E)$ is an instantaneous observer of rest mass $m$ moving with respect to instantaneous observer $T$ with speed $\tanh\vp$ in the direction $E$. Let $mZ_2=m(\cosh\vp\,T-\sinh\vp\,E)$ be another instantaneous observer moving with respect to $T$ with speed $\tanh\vp$ in the direction $-E$. If these two material particles collide they form a material particle $Z$ of rest mass $M$. Determine the velocity of $Z$ with respect to $T$ and its rest mass.
Energy and momentum of an instantaneous observer $mX$ of rest mass $m$ with respect to an instantaneous observer $MZ$ of rest mass $M$ are defined by $\b\colon=-\la mX,Z\ra$ and $P=mX+\la mX,Z\ra Z$.
Just to get a grasp of dimensions: in SI-units the rest energy of just $1g$ of mass is about $25GWh$. So it takes just $500g$ to get an equivalent of the daily electric energy produced in the US.

Adding/subtracting velocities

Suppose $X,Z$ und $T$ are instantaneous observers and we know the velocities of $X$ and $Z$ with respect to $T$. What is the velocity of $X$ with respect to $Z$? So we know that for some unit vectors $E,F\in T^\perp$ and real numbers $u,v\in[0,1)$: $$ Z=\b(T+vE),\quad X=\g(T+uF) $$ where $\b^2=1/(1-v^2)$ and $\g^2=1/(1-u^2)$. The energy of $X$ with respect to $Z$ is $$ -\la X,Z\ra=\b\g(1-uv\la E,F\ra) $$ and the momentum $P$ (of $X$ with respect to $Z$): $$ P\colon=X+\la X,Z\ra Z~. $$ Thus the velocity $W$ of $X$ with respect to $Z$ can be calculated: $$ W=\frac{P}{-\la X,Z\ra}~. $$ However we only calculate the norm of this velocity $W$: since $\Vert P\Vert^2=-1+\la X,Z\ra^2$ and $\Vert E\Vert=\Vert F\Vert=1$, we get: \begin{eqnarray*} \Vert W\Vert^2 &=&\frac{\la P,P\ra}{\la X,Z\ra^2} =\frac{\la X,Z\ra^2-1}{\la X,Z\ra^2} =\frac{(1-uv\la E,F\ra)^2-(1-u^2)(1-v^2)}{(1-uv\la E,F\ra)^2}\\ &=&\frac{u^2+v^2-2uv\la E,F\ra-u^2v^2(1-\la E,F\ra^2)} {(1-uv\la E,F\ra)^2} \end{eqnarray*} We single out three particular cases and compare them with the classical results: 1. $E=F$, which implies: $$ \Vert W\Vert=\Big|\frac{u-v}{1-uv}\Big|\geq|u-v| $$ 2. $F=-E$, in which case we get: $$ \Vert W\Vert=\frac{u+v}{1+uv}\leq u+v $$ and 3. $F\perp E$: $$ \Vert W\Vert=\sqrt{u^2+v^2-u^2v^2}\leq\sqrt{u^2+v^2}~. $$ These are not at all important results, but circulate constantly in text books under the name: subtraction or addition of velocities. It's much more important to keep in mind that any velocity is meant with respect to some instantaneous observer. Hence if several observers are involved for any velocity the respective pair of observers must always be specified.
Suppose $X,Z$ und $T$ are instantaneous observers and we know the velocity of $X$ with respect to $Z$ and the velocity of $Z$ with respect to $T$. What is the velocity of $X$ with respect to $T$? Suggested solution.

Observer Fields on Local Lorentz Manifolds

As the header may adumbrate this section is some sort of digression to local spacetimes.

Time orientation and observer fields

Suppose $Z$ is a vector field (cf. section) on a local Lorentz manifold $(M,\la.,.\ra)$, such that for all $x\in M$ we have $\la Z,Z\ra_x=-1$. Then $Z$ is said to define a time orientation and $(M,\la.,.\ra,Z)$ is called a local time oriented Lorentz manifold or a local spacetime. The coordinate field $E^0$ defines a time orientation on Minkowski space - we will always endow this space with this time orientation.
Given a time orientation $Z$ on the local Lorentz manifold $(M,\la.,.\ra)$ we say that a vector field $X$ is an observer field if
  1. For all $x\in M$ the tangent vector $X_x$ is an instantaneous observer, i.e. $\la X,X\ra_x=-1$.
  2. For all $x\in M$ the tangent vector $X_x$ is future pointing, i.e. $\la X,Z\ra_x < 0$.
Hence an observer field is a bunch of instantaneous observers: at each point of spacetime we have an instantaneous observer. The energy, momentum and velocity of an observer field $X$ with respect to another observer field $Z$ at $x\in M$ is simply the energy, momentum and velocity of an instantaneous observer $X_x$ with respect to the instantaneous observer $Z_x$. Hence the energy of $Y$ with respect to $X$ is a function $e:M\rar\R$: $$ e(x)\colon=-\la X_x,Y_x\ra=-\la X,Y\ra_x \quad\mbox{i.e.}\quad e=-\la X,Y\ra $$ and the momentum of $Y$ with respect to $X$ is a vector field $P\colon=Y+\la Y,X\ra X$, which is always orthogonal to $X$. In Minkowski space a vector field $$ X_x=\sum_{j=0}^n\z_j(x)\,E_x^j $$ is an observer field iff $$ -\z_0(x)^2+\z_1(x)^2+\cdots+\z_n(x)^2=-1 \quad\mbox{and}\quad \z_0(x) > 0~. $$

Rest spaces of observer fields

Given an observer field $Z$ on a time oriented Lorentz manifold $M$, there need not be a submanifold $M_Z$ of $M$ such that for all $m\in M_Z$: $T_mM_Z=Z^\perp$. Cf. e.g. Frobenius Theorem.
The vector field $Z\colon=E^0+x_2E^1$ is a time like vector field on the subset $U\colon=\{(x_0,x_1,x_2):|x_2| < 1\}$ of Minkowski space $\R_1^3$. Show that there is no function $f:U\rar\R$ such that $Z$ is normal to the submanifold $[f=0]$. Suggested solution.
Whenever such an $M_Z$ exists, it's Riemannian and it is called a rest space of $Z$ - mathematicians call it an integral manifold for $Z^\perp$. In this case we may define the distance of two events $x,y\in M_Z$ for $Z$ by the Riemannian distance of these points in the Riemannian manifold $M_Z$. Also any two events $x,y\in M_Z$ are said to be simultaneous events for $Z$.
For any $c\in\R$ the submanifold $[x_0=c]$ is a rest space of the observer field $Z\colon=E^0$ in Minkowski space $\R_1^{n+1}$. What is the distance of two points in $[x_0=c]$ for $Z$?
The observer $$ \t\mapsto(\t\b,R\cos(\o\t\b),R\sin(\o\t\b)) \quad\mbox{where}\quad \b\colon=1/\sqrt{1-R^2\o^2} $$ in exam is said to move with constant angular velocity $\o$ on a circle of radius $R$ with respect to $Z\colon=E^0$, because the curve $\t\mapsto(R\cos(\o\t\b),R\sin(\o\t\b))$ describes a circle of radius $R$ in the Euclidean manifold $M_Z$!
Usually objects are described in rest spaces of observer fields. In the subsequent example the object is a rod: Given two observer fields $T$ and $Z$ in the Lorentz manifold $M$. Assume $M_T$ and $M_Z$ are integral manifolds for $T^\perp$ and $Z^\perp$, respectively. The endpoints of a rod in $M_T$ are two world lines $c_0:I\rar M$ and $c_1:I\rar M$ such that $p_0\colon=c_0(0), p_1\colon=c_1(0)\in M_T$. If these two world lines intersect $M_Z$ in exactly two points $q_0$ and $q_1$, then you may call $d(q_0,q_1)/d(p_0,p_1)$ the lenght ratio. This will be quite different to the 'lenght ratio' that we are going to encounter in section: it will be about the perception of two different instantaneous observers at the same event!
$T=E^0$ and $Z=\cosh(\vp)E^0+\sinh(\vp)E^1$ are two observer fields in Minkowski space $\R_1^3$. $M_T\colon=[x_0=0]$ and $M_Z\colon=[-x_0\cosh(\vp)+x_1\sinh(\vp)=0]$ are integral manifolds for $T^\perp$ and $Z^\perp$, respectively. Compute the length ratio for $p_0=0$ and $p_1=(0,L_1,L_2)$. This very particular ratio is usually called Lorentz contraction factor of length!
$c_0(t)=(t,0,0)$ and $c_1(t)=(t,L_1,L_2)$ intersects $M_Z$ in $q_1=(t_1,L_1,L_2)$ and $-t_1\cosh(\vp)+L_1\sinh(\vp)=0$, i.e. $t_1=L_1\tanh(\vp)$. Hence the distance of $q_0=c_0(0)$ and $q_1$ in $M_Z$ is $$ \sqrt{-L_1^2\tanh^2\vp+L_1^2+L_2^2} =\sqrt{(1-\tanh^2\vp)L_1^2+L_2^2} $$ For e.g. $L_2=0$ we recover the well known contraction factor $\sqrt{1-v^2}$ as $v=\tanh\vp$ is the speed of $Z$ with respect to $T$. For $L_1=0$ we see that there is no contraction - the contraction factor is $1$.
The computation of the distance of the points $q_0$ and $q_1$ in the previous example turned out to be so easy because the space $M_Z$ was Euclidean and thus the distance of two points in $M_Z$ is just the norm $\Vert q_1-q_0\Vert$, which equals the Lorenth-length of the curve $t\mapsto(1-t)q_0+tq_1$ defined in exam. There is still another situation where the distances can be calculated easily: for one dimensional submanifolds $M_Z$!
Verify that for $0 < a < 1$ the vector field $Z\colon=-(x_0/a^2)E^0-x_1E^1$ is time-like on $M_Z\colon=\{(x_0,x_1)\in\R_1^2:(x_0/a)^2-x_1^2=1\}$ and $M_Z$ is a rest space for the nortmalized field $Z^0\colon=Z/\sqrt{-\la Z,Z\ra}$. For $T > 1$ the length of the curve joining $(a,0)$ and $(Ta,\sqrt{T^2-1})$ in the Riemannian manifold $M_Z$ and the Lorentz-length of this curve coincide.
In the general case we need to find a geodesic in $M_Z$ joining $q_0$ and $q_1$, which can be quite involved.

Observers and world lines

Any trajectory $c:\R\rar M$ of an observer field $X$ is an observer: this is because $c^\prime(t)=X_{c(t)}$ and thus $\la c^\prime(t),c^\prime(t)\ra_{c(t)}=-1$. Obviously, the energy, momentum and velocity of an observer $c$ with respect to an observer field $Z$ at $c(t)$ is defined by the energy, momentum and velocity of an instantaneous observer $c^\prime(t)$ with respect to the instantaneous observer $Z_{c(t)}$. Let us have a look at the example presented in exam: For $|R\o| < 1$ the curve $c(s)=(s,R\cos(\o s),R\sin(\o s))$ is a world line in three dimensional Minkowski space. Parametrizing by its proper time we get an observer $$ k:\t\mapsto(\t\b,R\cos(\o\t\b),R\sin(\o\t\b)) \quad\mbox{where}\quad \b\colon=1/\sqrt{1-R^2\o^2} $$ The energy $\b(\t)$ of this observer with respect to the observer field $E^0$ at a particular point $x\colon=k(\t)$ is by \eqref{iobeq3}: $-\la k^\prime(\t),E^0\ra$ - that's the energy of the instantaneous observer $k^\prime(\t)$ with respect to the instantaneous observer $E_{k(\t)}^0$; in our case we get: $\b(\t)=\b$ is constant. Analogously momentum $P(\t)$ and velocity $V(\t)$ of $k$ with respect to $E^0$ at $x\colon=k(\t)$ are momentum and velocity, respectively, of the instantaneous observer $k^\prime(\t)$ with respect to the instantaneous observer $E_x^0$, i.e. by e.g. \eqref{iobeq3} and \eqref{iobeq4} $$ P(\t)=k^\prime(\t)+\la k^\prime(\t),E^0\ra E_{k(\t)}^0 \quad\mbox{and}\quad V(\t)=P(\t)/\b(\t) $$ Hence we get in our particular example: $$ k^\prime(\t)=\b(E_x^0-R\o\sin(\o\t\b)E_x^1+R\o\cos/\o\t\b)E_x^2), $$ which implies $$ P(\t)=R\o\b(-\sin(\o\t\b)E_x^1+\cos(\o\t\b)E_x^2),\quad V(\t)=R\o(-\sin(\o\t\b)E_x^1+\cos(\o\t\b)E_x^2),\quad \norm{V(\t)}=|R\o|~. $$ Physicists say: $k$ moves with respect to $E^0$ with constant angular velocity. The observer $k_0(s)=(s,R,0)$ is at rest for $E^0$, because its velocity with respect to $E^0$ vanishes, and it meets the observer $k$ at the events $(2\pi n/\o,R,0)$, $n\in\Z$. The proper time elapsed between two consecutive meetings is $2\pi/\o$ for $k_0$ and $2\pi\sqrt{1-R^2\o^2}/\o$ for $k$.
For $R > 0$ put $M\colon=\R\times(R,\infty)$ and $h:M\rar\R^+$ any smooth function. At $(t,r)\in M$ we define $$ \la E^t,E^t\ra=-h(t,r),\quad \la E^r,E^r\ra=1/h(t,r) \quad\mbox{and}\quad \la E^t,E^r\ra=0~. $$ Then $(M,\la.,.\ra)$ is a local Lorentz manifold and $Z\colon=(1/\sqrt h)\,E^t$ defines a time orientation. For an observer $c(s)\colon=(t(s),r(s))$ we have $c^\prime=t^\prime\,E^t+r^\prime\,E^r$ and $-h(t,r)t^{\prime2}+r^{\prime2}/h(t,r)=-1$. Verify that for $v > 0$ the tangent vector $V\colon=-v(r^\prime/h(t,r)\,E^t+t^\prime h(t,r)\,E^r)$ at $c(s)$ is orthogonal to $c^\prime(s)$ and its norm is $v$. Determine the velocity of $c$ with respect to $Z$. For $h(r)\colon=1-R/r$ this metric is the so called 'radial part' of the Schwarzschild metric.
We have $\la Z,Z\ra=-1$ and $$ \la c^\prime,V\ra =-ht^\prime(-vr^\prime/h)+(1/h)r^\prime vt^\prime h =0 $$ i.e. $V_{c(s)}$ is orthogonal to $c^\prime(s)$. The energy and momentum of $c$ with respect to $Z$ at $c(s)$ are $\b\colon=-\la c^\prime,Z\ra=\sqrt ht^\prime$ and $$ P\colon=c^\prime+\la c^\prime,Z\ra Z =c^\prime-\sqrt ht^\prime(1/\sqrt h)\,E^t =r^\prime\,E^r~. $$ Finally we get for the velocity $W$ of $c$ with respect to $Z$: $$ W_{c(s)}=P_{c(s)}/\b =\frac{r^\prime(s)}{t^\prime(s)\sqrt{h(t(s),r(s))}}\,E_{c(s)}^r~. $$
Put $M\colon=\R^{n+1}$ and $h:M\rar\R^+$ any smooth function. At $x\in M$ we define $$ \la E^0,E^0\ra=-1,\quad \la E^j,E^j\ra=h(x)~. $$ Then $(M,\la.,.\ra)$ is a local Lorentz manifold - Einstein-de Sitter spacetime - and $Z\colon=E^0$ defines a time orientation.
Usually an observer is just given by a world line $c:t\mapsto c(t)$ and we don't want to calculate its proper time parametrization $k:\t\mapsto k(\t)$, which is given by $k(\t)=c(t(\t))$, where $\t\mapsto t(\t)$ denotes the inverse of $t\mapsto\t(t)$. The last function satisfies $$ \t^\prime(t)=\sqrt{-\la c^\prime(t),c^\prime(t)\ra} \quad\mbox{hence}\quad t^\prime(\t)=\frac1{\t^\prime(t)}=\frac1{\sqrt{-\la c^\prime(t),c^\prime(t)\ra}}~. $$ By the chain rule we have $k^\prime(\t)=c^\prime(t)t^\prime(\t)$ and thus we get for the energy of $c$ at the point $x\colon=c(t)=k(\t)$: \begin{equation}\label{ofleq1}\tag{OFL1} \b(t) =-\la Z,k^\prime(\t)\ra =\frac{-\la Z,c^\prime(t)\ra}{\sqrt{-\la c^\prime(t),c^\prime(t)\ra}} \end{equation} The momentum of $c$ with respect to $Z$ at the point $x\colon=c(t)=k(\t)$: \begin{equation}\label{ofleq2}\tag{OFL2} P(t) =k^\prime(\t)+\la k^\prime(\t),Z\ra Z_{k(\t)} =\frac{c^\prime(t)+\la c^\prime(t),Z\ra Z_{c(t)}}{\sqrt{-\la c^\prime(t),c^\prime(t)\ra}} \end{equation} and finally for the velocity of the observer with respect to $Z$ at the point $x\colon=c(t)=k(\t)$: \begin{equation}\label{ofleq3}\tag{OFL3} V(t) =\frac{c^\prime(t)+\la c^\prime(t),Z\ra Z_{c(t)}}{-\la Z,c^\prime(t)\ra} \end{equation} Thus all quantities (energy cf. \eqref{ofleq1}, momentum cf. \eqref{ofleq2}, velocity cf. \eqref{ofleq3}) can be calculated without knowing the proper time at all!
The observer in exam moves with respect to $E^0$ with velocity $atE^1$ - physicists say that the observer moves with constant acceleration $a$ in direction $E^1$ (for $E^0$). The time elapsed for the observer until reaching speed $1$ is: $\pi/4a$, which is less than the classical answer: $1/a$. In SI-units: accelerating by $1g$ it takes about one year to get at the speed of light.
By \eqref{ofleq3} the velocity of the observer at $c(t)=(t,at^2/2)$ with respect to $E^0$ is: $$ V(t)=\frac{E^0+atE^1-E^0}{-\la E^0,E^0+atE^1\ra}=atE^1~. $$ The second assertion follows immediately from the formula for the proper time in exam.
If $Z$ is an observer field on a local Lorentz manifold $(M,\la.,.\ra)$ and $E$ denotes a unit vector field orthogonal to $Z$, then for any pair of smooth functions $a,b:M\rar\R$ the vector fields $X\colon=\cosh(a)Z+\sinh(a)E$ and $Y\colon=\cosh(b)Z+\sinh(b)E$ are observer fields and by exam energy, momentum, velocity and speed of $Y$ with respect to $X$ are given by $$ \cosh(b-a),\quad \sinh(b-a)(\sinh(a)Z+\cosh(a)E),\quad \tanh(b-a)(\sinh(a)Z+\cosh(a)E),\quad |\tanh(b-a)|~. $$
Compute the velocity of $c(t)=(e^t-1,t+t^2/2)$ in $2$-dimensional Minkowski space $M$ with respect to the observer field $Z_x\colon=\cosh(x_0)E_x^0+\sinh(x_0)E_x^1$ at each point $c(t)$, $t\geq0$.
Let $c:[a,b]\rar M$ be a smooth curve in Minkowski space $M$ such that for all $t\in[a,b]$: $c^\prime(t)$ is time-like and future pointing. Then $$ T(c)\colon=\int_a^b\Vert c^\prime(t)\Vert\,dt $$ is the proper time of the curve. Show that for any smooth curve $c:[0,1]\rar M$ such that $c^\prime(t)$ is time-like and future pointing and $c(0)=0$ and $c(1)=(1,0,\ldots,0)$: $T(c)\leq1$. Suggested solution. Typically in Lorentz manifolds 'time-like geodesics' are characterized by maximal proper time. In relativity these curves are called freely falling observers. So the local time-axis of a freely falling observer is the 'longest time-like and future pointing direction' in $M$.
Frequently found formulations like: an observerer moves with respect to an observer at rest with some velocity are literally nonsense, they are sort of short hand for: at any event $x$ of a local Lorentz manifold $M$ an instantaneous observer $X_x$ moves with respect to another instantaneous observer $Z_x$ with velocity $V_x$. These assumptions determine $X_x$ given $Z_x$ and $V_x$ by \eqref{iobeq5}: $$ X_x=\b(x)(Z_x+V_x) \quad\mbox{and}\quad \b(x)=1/\sqrt{1-\Vert V_x\Vert^2}~. $$ So strictly speaking you are given an observer field $Z$ and a vector field $V$ satisfying for all $x\in M$: $V_x\perp Z_x$ and $\Vert V_x\Vert < 1$. Remember an observer is in our terminolgy a trajectory of an observer field and the velocity of one observer $t\mapsto c(t)$ with respect to another observer $s\mapsto k(s)$ only makes sense in points $x$ where $x=c(t)=k(s)$. In these points the velocity of the observer $t\mapsto c(t)$ with respect to the observer $s\mapsto k(s)$ is defined by the velocity of the instantanetous observer $c^\prime(t)$ with respect to the instantanetous observer $k^\prime(s)$.

Minkowski force

Force is one of the essential concepts of classical physics, it's simply the change in momentum. The reletivistic counterpart is the change of energy-momentum: Let $s\mapsto c(s)$ be an observer in a local time-oriented Lorentz manifold $(M,\la.,.\ra, Z)$. Classically the force is just the change of the momentum per unit time. Relativistically we'd like to define the Minkowski force as the change of the energy-momentum vector $c^\prime(s)$ relative to the change of proper time. So we need some sort of second derivative. However, we cannot define $$ \lim_{h\to0}\frac1h(c^\prime(s+h)-c^\prime(s)) $$ because $c^\prime(s)\in T_{c(s)}M$ and $c^\prime(s+h)\in T_{c(s+h)}M$. The notion of 'parallel transport' will overcome this problem. In general it's defined along any curve $s\mapsto c(s)$ as a smooth mapping $s\mapsto P_s$, where $P_s$ is a linear isometry of the Lorentz space $(T_{c(0)},\la.,.\ra_{c(0)})$ onto the Lorentz space $(T_{c(s)},\la.,.\ra_{c(s)})$ such that $P_0=1$. In general it depends on the curve $c$ (cf. exam): $$ \bnabla c^\prime(s) \colon=\lim_{h\to0}\frac1h\Big(P_{c(s+h)\to c(s)}c^\prime(s+h)-c^\prime(s)\Big),\quad P_{c(s+h)\to c(s)}\colon=P_sP_{s+h}^{-1}~. $$ This is called the Minkowski force or the covariant derivative of $c^\prime$ along the curve $c$. By means of this kind of transport you may compare observers perception at different events; however we won't pursue this sort of comparison!
It's characteristic for Minkowski space that parallel transport doesn't depend on the curve and is simply given by $P_s(E_{c(0)}^j)=E_{c(s)}^j$; in this case we get: $$ \bnabla c^\prime(s)=\sum_j c_j^\dprime(s)E_{c(s)}^j~. $$ Parallel transport is an essential notion in Pseudo-Riemannian geometry, in particular $\bnabla c^\prime=0$ is just the definition of a geodesic; in particular: if $c$ is a geodesic, then the parallel transport of $c^\prime(0)$ along $c$ is given by $c^\prime(s)$ - cf. exam. On the Riemannian manifold $S^2$ this can be used to visualize parallel transport along great circles, i.e. geodesics:
Verify that parallel transport on $S^2$ depends on the curve. Suggested solution.
Moreover, in the Lorentz case a time-like curve is a geodesic if and only if the Minkowski force vanishes; hence it's called a freely falling observer.
Suppose $X$ is a vector field along a curve $c:s\mapsto c(s)$, i.e. $X(s)\in T_{c(s)}M$ and $s\mapsto X(s)$ is smooth. Show that $$ \lim_{s\to0}\frac1s(X(s)-P_sX(0)) =\lim_{s\to0}\frac1s(P_s^{-1}X(s)-X(0)) $$ and this is called the covariant derivative $\bnabla X(0)$ of $X$ (at $s=0$) along the curve $c$.
Suppose $X,Y$ are vector fields along a curve $c:s\mapsto c(s)$. Show that $$ \ttd s\la X(s),Y(s)\ra =\la\bnabla X(s),Y(s)\ra+\la X(s),\bnabla Y(s)\ra~. $$ 2. If $f$ is a smooth functions of $s$, then $$ \bnabla(fX)(s)=f^\prime(s)X(s)+f(s)\bnabla X(s)~. $$ 3. For any $v\in T_{c(0)}M$ the mapping $J:s\mapsto P_s(v)$ is a vector field along $c$ and $\bnabla J(s)=0$. Conversely if $X$ is a vector field along $c$ such that $\bnabla X(s)=0$, then $X(s)=P_s(X(0))$. Thus the parallel transport of a vector $v\in T_{c(0)}M$ along $c$ is uniquely defined by $\bnabla X(s)=0$ and $X(0)=v$. Suggested solution.
If $c:s\mapsto c(s)$ is a geodesic in the Pseudo-Riemannian manifold $M$, then $s\mapsto\la c^\prime(s),c^\prime(s)\ra$ is constant. Hence the curve is parametrized proportional to 'length'!
From exam we conclude that $$ \ttd s\la c^\prime(s),c^\prime(s)\ra =2\la\bnabla c^\prime(s),c^\prime(s)\ra=0~. $$ In the Minkowski case the geodesic equation $\bnabla c^\prime(s)=0$ comes down to: $c_j^\dprime=0$ for all $j$, i.e. $c_j(s)=a_j+k_js$ for some $a_j,k_j\in\R$; this is what is usually called a straight line (parametrized by its proper time $s$). Physicists say: in Minkowski space the world line of a freely falling observer is a straight line (parametrized by its proper time).
In a Lorentz manifold a geodesic $c:s\mapsto c(s)$ is either time-like for all $s$ or space-like for all $s$ or light-like for all $s$.
As for the Minkowski force $F(\t)\colon=\bnabla c^\prime(\t)$ of an observer $c:\t\mapsto c(\t)$ at proper time $\t$ exam implies that $F(\t)$ is in the rest space of $c^\prime(\t)$, because: $$ 0=\frac12\ttd{\t}\la c^\prime(\t),c^\prime(\t)\ra =\la\bnabla c^\prime(\t),c^\prime(\t)\ra $$ The Minkowski force of an observe $c:\t\mapsto c(\t)$ with respect to an observer field $Z$ is defined as the orthogonal projection of $\bnabla c^\prime$ on the rest space $Z^\perp$ at the point $c(\t)$, i.e. $$ F_{c(\t)}=\bnabla c^\prime(\t)+\la\bnabla c^\prime(\t),Z\ra Z_{c(\t)}~. $$
Compute the Minkowski force of the observer $$ k:\t\mapsto(\t\b,R\cos(\o\t\b),R\sin(\o\t\b)) \quad\mbox{where}\quad \b\colon=1/\sqrt{1-R^2\o^2} $$ in Minkowski space $\R_1^3$. Show that $k$ has constant speed $|R\o|$ with respect to $E^0$. What is the Minkowski force of the observer $k$ with respect to the observer field $T\colon=\g(E^0+vE^1)$?
Energy and momentum of $k$ with respect to $E^0$ at $k(\t)$ are $\b$ and $R\o\b(-\sin(\o\t\b)\,E^1+\cos(\o\t\b)\,E^2)$ respectively. Hence we get for the speed of $k$ with respect to $E^0$ at any point: $|R\o|$. The Minkowski force is $-R\o^2\b^2(\cos(\o\t\b)E^1+\sin(\o\t\b)E^2)$. Finally we get for the Minkowski force of the observer $k$ with respect to the observer field $T\colon=\g(E^0+vE^1)$: \begin{eqnarray*} &&-R\o^2\b^2(\cos(\o\t\b)E^1+\sin(\o\t\b)E^2) -\la R\o^2\b^2(\cos(\o\t\b)E^1+\sin(\o\t\b)E^2),\g(E^0+vE^1)\ra\g(E^0+vE^1)\\ &=&-R\o^2\b^2(\cos(\o\t\b)E^1+\sin(\o\t\b)E^2) -R\o^2\b^2\g^2 v\cos(\o\t\b)(E^0+vE^1) \end{eqnarray*}
Compute the Minkowski force of a world line $c:t\mapsto c(t)$ (i.e. $c$ is not necessarily parametrized by proper time $\t$) in Minkowski space $\R_1^{n+1}$.
The geodesic equation describes a freely falling observer, which means that the Minkowski force on the observer vanishes. Let us now discuss a more intricate case: the rocket equation. Suppose $s$ denotes the proper time of a rocket, i.e. an observer $s\mapsto c(s)$ in a local Lorentz manifold driven by the exhaust of gas, photons or whatsoever. This process reduces the initial mass $M_0\colon=M(0)$ of the rocket. Let $X(s)=c^\prime(s)$ and $Y(s)\in T_{c(s)}M$ be the normalized energy-momentum vectors of the rocket and the exhaust, respectively, so we assume that the exhaust is not light-like. At proper time $s$ the mass of the rocket is $M(s)$ and therefore its energy-momentum at event $c(s)$ is: $p(s)=M(s)X(s)$. At proper time $s+h$ the energy-momentum vector of the rocket is: $(M(s)-\D M)X(s+h)$ and the energy-momentum vector of the exhaust is (up to first order): $\D mY(s)$ - unlike the classical case there is no reason to assume that $\D m=\D M$! Therefore we get for the Minkowski force (as the covariant derivative of $p$ along $c$): $$ \lim_{h\to0}\frac1h\Big( P_{c(s+h)\to c(s)}\Big((M(s)-\D M)X(s+h)\Big)-M(s)X(s)+\D m Y(s)\Big)~. $$ Now, as $h$ tends to $0$ we have: $\lim_{h\to0}\D M/h=-M^\prime$ and $\lim_{h\to0}\D m/h=m^\prime$ and therefore the Minkowski force vanishes (i.e. the energy-momentum vector is conserved) if and only if: \begin{equation}\label{ofleq4}\tag{OFL4} M\bnabla X+M^\prime X+m^\prime Y=0 \quad\mbox{or}\quad \bnabla(MX)+m^\prime Y=0 \end{equation} As $\la X,X\ra=-1$ it follows by exam that $\bnabla X\perp X$ and thus we get the energy equation of a rocket: $$ -M^\prime+m^\prime\la X,Y\ra=0 \quad\mbox{or}\quad M^\prime=-\b m^\prime, $$ where $\b\colon=-\la X,Y\ra$ denotes the energy of $Y$ with respect to $X$; projecting \eqref{ofleq4} orthogonally on $X^\perp$, we get the rocket equation: \begin{equation}\label{ofleq5}\tag{OFL5} M\bnabla X=-m^\prime Y^X =M^\prime(Y^X/\b) =M^\prime V \end{equation} where $Y^X$ is the orthogonal projection of $Y$ on $X^\perp$ and $V\colon=Y^X/\b$ is the velocity of the exhaust with respect to $X$.
Deduce from the energy equation that $s\mapsto M(s)+m(s)$ is strictly decreasing if for all $s$: $V(s)\neq0$.
Deduce from the rocket equation that $$ M\la\bnabla X,V\ra=M^\prime\norm V^2~. $$
Deduce the rocket equation if the exhaust consists solely of photons.
The classical (i.e. Riemannian) rocket equation doesn't differ from \eqref{ofleq5}: we simply have to change to the Riemannian setting and look at $X(s)\colon=c^\prime(s)$ as the velocity of the rocket, i.e. in this case $c$ is the path of the rocket. For example, in the Euclidean case the rocket equation comes down to: $Mc^\dprime=M^\prime V$.
We emphasize that the relativistic rocket equation \eqref{ofleq5} holds in any Lorentz manifold. Unlike the classical equation, which needs some additional terms in case the rocket moves in a gravitational field, the relativistic equation doesn't change at all, because gravity is encoded in the Lorentz metric! In relativity gravitation is not a force that acts in a predetermined space, gravitation rather is the space or the spacetime itself. It is a Lorentz metric on a four dimensional manifold. Moreover, it's a particular Lorentz metric, determined by what is known as Einstein's field equations. Similar to the classical case, where the mass- or energy density defines the gravitational potential via Poisson's equation, a sort of energy distribution (actually a stress tensor field) determines the Lorentz metric via Einstein's field equations. Minkowski space is just a model of spacetime with vanishing stress tensor field.
It's worth mentioning that Newtonian mechanics itself can be geometrized in this direction: classically the equation of motion in a potential $U$ (in Euclidean space) is given by $c^\dprime+\nabla U=0$. Does there exist a Riemannian metric $g$ conformal to the canonical Euclidean metric (i.e. $g(X,Y)_x=e^{f(x)}\can(X,Y)$ for some smooth function $f$) such that the geodesic equation $\bnabla c^\prime=0$ with respect to $g$ is equivalent to the equation of motion $c^\dprime+\nabla U=0$? This actually holds: if $c(0)$ lies on a submanifold $M_E$ of the form $\{x:\Vert x\Vert^2/2+U(x)=E\}$, $E\in\R$, then the whole curve lies in $M_E$ - that's the classical conservation of energy! Now for each real value $E$ there is a function $f$ such that the geodesics on $(M_E,g)$ are exactly the solutions $c$ of the equation of motion satisfying $c(0)\in M_E$.

Rocket in Minkowski space

We will finally assume that
  1. We are in Minkowski space and $Z=E^0$.
  2. The norm of the velocity $V$ with respect to the rocket is constant, i.e. $\norm V=v$.
  3. The rocket moves in direction of $E^1$ for $E^0$ and the exhaust in direction $-E^1$.
By 1. and 3. we can write: $$ X(s)=\cosh(\vp(s))E_{c(s)}^0+\sinh(\vp(s))E_{c(s)}^1 \quad\mbox{and}\quad Y(s)=\cosh(\phi(s))E_{c(s)}^0+\sinh(\phi(s))E_{c(s)}^1~. $$ where $|\tanh(\vp(s))|$ is the speed of the rocket with respect to $E^0$. In Minkowski space it follows that $$ \bnabla X(s)=\vp^\prime(s)\Big(\sinh(\vp(s))E_{c(s)}^0+\cosh(\vp(s))E_{c(s)}^1\Big)~. $$ Assuming 2. and 3. we get by exam: $$ V(s)=-v\Big(\sinh(\vp(s))E_{c(s)}^0+\cosh(\vp(s))E_{c(s)}^1\Big) \quad\mbox{and}\quad v=|\tanh(\phi(s)-\vp(s))|~. $$ Hence the rocket equation \eqref{ofleq5} comes down to: $M\vp^\prime=-vM^\prime$, i.e.: $\vp(s)=v\log(M_0/M(s))$. For given mass $M$ of the rocket its speed with respect to $E^0$ is $$ \tanh\Big(v\log\frac{M_0}M\Big)~. $$ For small values of the argument this simplifies to the classical result: $$ v\log\frac{M_0}M~. $$
Compute the speed of the exhaust with respect to $E^0$.
The speed of sound is approximately $10^{-6}$. Thus if $v$ is thousand times the speed of sound the rocket reaches 1% the speed of light approximately when $M/M_0=10^{-4}$. Hence almost all mass must be fuel.

Covariant derivatives on submanifolds

Suppose $N$ is a submanifold of a local Pseudo-Riemannian manifold $M$. The covariant derivative of a vector field $s\mapsto X(s)$ along a curve $s\mapsto c(s)$ in $N$ is the orthogonal projection of the covariant derivative of $s\mapsto X(s)$ along the curve $s\mapsto c(s)$ in $M$ on the subspace $T_{c(s)}N$ of $T_{c(s)}M$.
For example, given a curve $c$ on $N\colon=S^{n-1}$ and a vector field $X$ along $c$ in $N=S^{n-1}$, i.e. $$ X(s)=\sum_j\z_j(s)\,E_{c(s)}^j \quad\mbox{such that}\quad \sum_j\z_j(s)c_j(s)=0~. $$ Then the covariant derivative of $X$ along $c$ in $M=\R^n$ is given by $$ X^\prime(s)\colon=\sum_j\z_j^\prime(s)\,E_{c(s)}^j $$ and the covariant derivative of $X$ along $c$ in $N=S^{n-1}$ is given by $$ \bnabla X(s)=X^\prime(s)-\can(X^\prime(s),N(s))N(s) $$ where $N(s)\colon=\sum_jc_j(s)\,E_{c(s)}^j$ is the unit normal vector field.
A curve $c:I\rar S^{n-1}$ is a geodesic iff: $$ \forall j=1,\ldots,n:\quad c_j^\dprime=\sum_{k=1}^n c_k^\dprime c_kc_j~. $$
Compute the covariant derivative of $X(s)\colon=c^\prime(s)$ along $c(s)$ in $S^{n-1}$ as a submanifold of Euclidean space $\R^n$ for $$ c(s)\colon=(\cos(s),a_1\sin(s),\ldots,a_{n-1}\sin(s)) \quad\mbox{and}\quad \sum a_j^2=1~. $$
Compute the covariant derivative of $X(s)=c^\prime(s)$ along $c(s)$ in $H^n$ (cf. subsection) as a submanifold of Minkowski space $\R_1^{n+1}$ for $$ c(s)\colon=(\cosh(s),a_1\sinh(s),\ldots,a_n\sinh(s)) \quad\mbox{and}\quad \sum a_j^2=1~. $$ Conclude that $c$ is a geodesic in $H^n$.
We have $$ X(s)=\sinh(s)E_{c(s)}^0+\sum_ja_j\cosh(s)E_{c(s)}^j,\quad X^\prime(s)=\cosh(s)E_{c(s)}^0+\sum_ja_j\sinh(s)E_{c(s)}^j $$ and the normal field $N_x=x_0E_x^0+\sum x_jE_x^j$ $$ N(s) \colon=N_{c(s)} =\cosh(s)E_{c(s)}^0+\sum_ja_j\sinh(s)E_{c(s)}^j~. $$ It follows that the inner product of $X^\prime(s)$ and $N(s)$ is $-\cosh^2(s)+\sinh^2(s)=-1$ and thus (as $N(s)$ is time-like): $$ \bnabla X(s) =X^\prime(s)+\la X^\prime(s),N(s)\ra N(s) =X^\prime(s)-N(s)=0, $$ i.e. $\bnabla c^\prime=0$. Hence $c$ is a geodesic of $H^n$.
Find a light-like geodesic in the sumbanifold $\R\times S^{n-1}\colon=\{(x_0,x_1,\ldots,x_n)\in\R_1^{n+1}: x_1^2+\cdots+x_n^2=1\}$ of $\R_1^{n+1}$. Suggested solution.
Find all geodesics on the submanifold $S^{n-1}$ of Euclidean space $\R^n$.
By exam we may assume that $\sum c_j^{\prime2}=1$. Since $\sum c_j^{2}=1$ we conclude that $\sum c_j^{\prime}c_j=0$ and therefore $$ \sum c_j^{\dprime}c_j=-\sum c_j^{\prime2}=-1~. $$ By exam we thus get the equations: $$ \forall j=1,\ldots,n:\quad c_j^\dprime+c_j=0~. $$ Now suppose $\sum c_j(0)n_j=\sum c_j^\prime(0)n_j=0$, then $f(s)\colon=\sum c_j(s)n_j$ solves the initial value problem $f^\dprime+f=0$, $f(0)=f^\prime(0)=0$, i.e. by uniqueness of solutions to ODE: $f=0$ and thus the curve $c$ lies in the two dimensional plane spanned by $(c_1(0),\ldots,c_n(0))$ and $(c_1^\prime(0),\ldots,c_n^\prime(0))$. This shows that $c$ is a great circle on $S^{n-1}$.
Find all geodesics on the submanifold $H^n$ of Minkowski space $\R_1^{n+1}$.

Perception of Light

 In this section we are back to linear algebra, i.e. we are working in a fixed tangent space. Again we will use capital letters for vectors!

Aberration of light

For an instantaneous observer colors of an object are determined by the energies of arriving rays of light emanated or reflected by the object. Shape and size of the object for an instantaneous observer are fixed by the angles of these rays for the instantaneous observer. Effects concerning angles of light are usually called aberration of light (aberration means some sort of deviation from normal). So let $X,Y$ be light- or time-like and let $T$ be any instantaneous observer. $T$ doesn't observe $X$ or $Y$ directly, only their energies and their momenta. Denoting by $P$ and $Q$, respectively, the momenta of $X$ and $Y$ with respect to $T$ we define the angle $\a\in[0,\pi]$ of $X$ and $Y$ (observed by $T$) by the angle of the momenta $P$ and $Q$ in the rest space of $T$, i.e. $$ \cos\a=\frac{\la P,Q\ra}{\Vert P\Vert\Vert Q\Vert}~. $$ Of course, instead of momenta we could have taken velocities as well, so if $V$ and $W$ denote the velocities of $X$ and $Y$ with respect to $T$, then $$ \cos\a=\frac{\la V,W\ra}{\Vert V\Vert\Vert W\Vert}~. $$ How to calculate the angle in terms of the instantaneous observers $X$ and $Y$ and not in terms of momenta or velocities? This is done in the subsequent lemma:
For all instantaneous observers $T$ and all causal (i.e. time- or light-like) $X,Y$ the angle $\a\in[0,\pi]$ of $X$ and $Y$ for $T$ is given by: $$ \cos\a=\frac{\la X,Y\ra+\la X,T\ra\la Y,T\ra} {\sqrt{(\la X,X\ra+\la X,T\ra^2)(\la Y,Y\ra+\la Y,T\ra^2)}}~. $$
$\proof$ Since $P=X+\la X,T\ra T$, $Q=Y+\la Y,T\ra T$ and $\la T,T\ra=-1$ we get: $$ \la P,Q\ra =\la X,Y\ra+\la X,T\ra\la T,Y\ra+\la Y,T\ra\la T,X\ra-\la X,T\ra\la Y,T\ra =\la X,Y\ra+\la X,T\ra\la Y,T\ra $$ and thus $\Vert P\Vert^2=\la X,X\ra+\la X,T\ra^2$ and $\Vert Q\Vert^2=\la Y,Y\ra+\la Y,T\ra^2$. $\eofproof$
Many 'classical' derivation of relativistic formulas implicitely assume a sort of directional invariance: two instantaneous observers $X,Y$, who move into the same direction for some instantaneous observer $T$ also move into the same direction for another instantaneous observer $Z$. But that's not the case! This is because $X$ and $Y$ are in general not collinear. Again, neither the direction of movement nor the energy are universal (i.e. both depend on an instantaneous observer), it's only their composition as an instantaneous observer or a photon and these are vectors in a Lorentz space and not in a Euclidean space! Though 'pseudo-classical' derivations may get 'correct relativistic formulas', most of them omit a fundamental point! One example of this kind of explanation is the relativistic aberration formula, it's derivation is typically Euclidean (it somehow suggests that different instantaneous observers have the same 'space of perception') with relativistic ingredients (a relativistic formula for the addition of velocities). The essential part is hidden in the 'Lorentz transformation between two frames of reference' because this transformation maps the rest space of the first instantaneous observer onto the rest space of the second. Frame of reference simply means an orthonormal basis. Thus beware, arguments based on our geometric intuition are usually a bit ominous: most of them do not take into account or do not mention that different instantaneous observers have different rest spaces.
$X=\a(T+uE)$ and $Y=\b(T+vE)$ move into the same direction for $T$ but in general not for $Z=\g(T+wF)$ for e.g. $F\perp E$.
Since $\la X,Y\ra=-\a\b(1-uv)$, $\la X,Z\ra=-\a\g$, $\la Y,Z\ra=-\b\g$ and $\a^2(1-u^2)=\b^2(1-v^2)=\g^2(1-w^2)=1$, we get for the angle $\vp$ of $X$ and $Y$ for $Z$: \begin{eqnarray*} \cos\vp &=&\frac{\la X,Y\ra+\la X,Z\ra\la Y,Z\ra} {\sqrt{(\la X,X\ra+\la X,Z\ra^2)(\la Y,Y\ra+\la Y,Z\ra^2)}}\\ &=&\frac{\a\b(\g^2-1+uv)}{\sqrt{(-1+(\a\g)^2)(-1+(\b\g)^2)}} =\frac{w^2+uv(1-w^2)}{\sqrt{(w^2+u^2(1-w^2))(w^2+v^2(1-w^2))}}~. \end{eqnarray*} By Cauchy-Schwarz this is strictly smaller than $1$ for $u\neq v$.
The photons $X=\a(T+E)$ and $Y=\b(T+E)$ move into the same direction for $T$ and they move into the same direction for all instantaneous observers. This is because $X$ and $Y$ are collinear!
We are mostly interested in light-like vectors $X$ and $Y$. In this case the formula in lemma simplifies considerably and we get: \begin{equation}\label{pereq1}\tag{PER1} 2\sin^2(\a/2) =1-\cos\a =\frac{-\la X,Y\ra}{\la X,T\ra\la Y,T\ra}~. \end{equation} We immediately realize that in case the energies of $X$ and $Y$ for another instantaneous observer $Z$ are greater than the corresponding energies for $T$, then the angle observed by $Z$ is smaller than the angle observed by $T$: in this case the object appears smaller for $Z$ than for $T$.
Suppose we have a material particle $mT$ of rest mass $m$. A photon $Z$ of energy $\g_0$ (with respect to $mT$ or $T$, whatever you prefer) gets scattered by $mT$, i.e. $\g_0Z$ collides with $mT$ and the outcome is a material particle $mX$ of rest mass $m$ and a photon $\g W$ of energy $\g$. Deduced from the energy-momentum conservation: $\g_0Z+mT=mX+\g W$ that $$ \g_0-\g=\frac{-\g_0\g\la Z,W\ra}m=\frac{2\g_0\g\sin^2(\a/2)}m~. $$ where $\a$ is the angle of $Z$ and $W$ for $T$. Thus the energy $\g$ of the photon after the collision is always smaller or equal to $\g_0$. wikipedia. Suggested solution.
Here comes another straightforward application of \eqref{pereq1}:
Let $E,F$ be unit vectors in the rest space of $T$. The light-like vectors $X=T+F$ and $Y=T-F$ point into opposite directions for $T$. If $v\neq0$ and $F\neq\pm E$, then $X$ and $Y$ do not point into opposite directions for $Z\colon=\b(T+vE)$.
The angle $\a$ of $X$ any $Y$ for $Z$ is given by $$ \sin^2(\a/2) =-\frac{\la X,Y\ra}{2\la X,Z\ra\la Y,Z\ra} =\frac1{\b^2(1-v^2\la E,F\ra^2)}~. $$ If $v\neq0$ and $F\neq\pm E$, then $$ \sin^2(\a/2) < \frac1{\b^2(1-v^2)}=1~. $$ The following example discusses a more general situation.
Suppose $T,Z$ are instantaneous observers and $E,F,\ldots$ is an orthonormal basis for the rest space $T^\perp$. Assume $Z$ moves with respect to $T$ with velocity $vE$, i.e. $Z=\b(T+vE)$ and put for real numbers $e,f$ satisfying $e^2+f^2=1$: $X\colon=T+eE+fF$ and $Y\colon=T-eE+fF$ - i.e. $X$ and $Y$ are light rays in the directions $eE+fF$ and $-eE+fF$ (for $T$). If $\a_T$ is the angle of $X$ and $Y$ observed by $T$ and $\a_Z$ the angle observed by $Z$, then $$ \tan(\a_Z/2)=\frac1{\b}\tan(\a_T/2)~. $$ The factor $1/\b$ on the right is called the factor of contraction. This is one of the few cases where this factor only depends on the speed of $Z$!
In the picture below $C$ is light-like, for $T$ it's a ray of light in the direction of $F$.
light cone
Since $-\la X,T\ra=-\la Y,T\ra=1$, $-\la X,Z\ra=\b(1-ev)$ and $-\la Y,Z\ra=\b(1+ev)$, we conclude by \eqref{pereq1}: \begin{eqnarray*} \sin^2(\a_T/2) &=&-\frac{\la X,Y\ra}{2\la X,T\ra\la Y,T\ra} =-\frac{\la X,Y\ra}{2}\\ \sin^2(\a_Z/2) &=&-\frac{\la X,Y\ra}{2\la X,Z\ra\la Y,Z\ra} =-\frac{\la X,Y\ra}{2\b^2(1-e^2v^2)} \end{eqnarray*} and thus $$ \sin^2(\a_Z/2)=\frac{\sin^2(\a_T/2)}{\b^2(1-e^2v^2)}~. $$ Now $\b^2(1-v^2)=1$, $-\la X,Y\ra=-1-e^2+f^2=-2e^2$ and $\tan^2=\sin^2/\cos^2$ imply that $$ \tan(\a_Z/2)=\frac{\tan(\a_T/2)}{\b}~. $$
Let $\a_T$ and $\a_Z$, respectively, be the angles of $X$ and $C$ for $T$ and $Z$, respectively. Prove that $$ \sin(\a_Z/2)=\frac1{\b\sqrt{1-ev}}\sin(\a_T/2)~. $$ In this case the factor of contraction also depends on the direction of $X$! Suggested solution.
These two results exemplify that objects appear contracted in the direction of motion. However the factor of contraction not only depends on the direction of motion but also on the direction of the incident light! In exam this factor is always smaller than $1$; in exam this factor is larger than in exam and it is less than $1$ iff $v(v-e) > 0$. But for $0 < v < e$ we have $\a_Z > \a_T$, i.e. objects may appear even larger for $Z$ than for $T$. In summary, objects in the direction of motion of $Z$ don't appear contracted uniformly over their length! In fact it's impossible that contraction appears in all directions; this is because the following example shows that a contraction $F:S^2\rar S^2$ cannot be onto!
Suppose $(X,d)$ is a compact metric space and $F:X\rar X$ a mapping such that for all $x\neq y$: $d(F(x),F(y)) < d(x,y)$. Then $F$ is not onto. Suggested solution.
Suppose $(X,d)$ is a compact metric space and $F:X\rar X$ a surjection such that for all $x,y\in X$: $d(F(x),F(y))\leq d(x,y)$. Then $F$ is an isometry. Cf. Isometries in compact metric spaces. Suggested solution.
Suppose $(X,d)$ is a compact metric space and $F:X\rar X$ a continuous bijection such that for all $x,y\in X$: $d(F(x),F(y))\geq d(x,y)$. Then $F$ is an isometry.
Now assume $Z=\b(T+vF)$, i.e. $Z$ moves in the direction of $F$ (with respect to $T$). Retaining all other assumptions we get for the angle of $X=T+eE+fF$ and $Y=T-eE+fF$: $$ \sin(\a_Z/2)=\frac1{\b(1-fv)}\sin(\a_T/2) \quad\mbox{i.e.}\quad \tan(\a_Z/2)=\frac{f}{\b(f-v)}\tan(\a_T/2)~. $$ If $v < 0$ and $f > 0$, then $Z$ moves towards the directions of $X$ and $Y$ and $\a_Z$ is evidently smaller than $\a_T$: objects an observer moves toward appear smaller! The formula for $\tan(\a_Z/2)$ is usually refered to as the relativistic aberration formula, thought it's only a formula for a very special situation.
The angle of $X$ and $Y$ for $T$ is still $\a_T$. However, now $-\la X,Z\ra=\b(1-fv)$ and also $-\la Y,Z\ra=\b(1-fv)$ and thus the result follows by \eqref{pereq1}. Eventually $e^2+f^2=1$, $\b^2(1-v^2)=1$ and $\tan^2=\sin^2/(1-\sin^2)$ imply that $$ \tan^2(\a_Z/2) =\tan^2(\a_T/2)\frac{(1-e^2)(1-v^2)}{(1-vf)^2-e^2(1-v^2)} =\tan^2(\a_T/2)\frac{f^2(1-v^2)}{(f-v)^2}~. $$
Under which conditions on $f$ and $v\in(0,1)$ do we have: $\a_Z > \a_T$?
Suppose $Z=\b(T+vE)$, $X=T+F$, $Y=T+G$ such that $F,G\perp\lhull{E,T}$, i.e. $X$ and $Y$ are light-like normal to the direction of motion of $Z$. Show that the angle of $X$ and $Y$ is always smaller for $Z$ than for $T$.
Since $\la T,X\ra=\la T,Y\ra=-1$, $\la Z,X\ra=\la T,Y\ra=-\b$ and $\la X,Y\ra=-1+\la F,G\ra$, we conclude by \eqref{pereq1} that: $\sin(\a_Z/2)=\sin(\a_T/2)/\b$.
Suppose $Z=\b(T+vE)$, $X=T+fF+e_1E$, $Y=T+gG+e_2E$ such that $F,G\perp\lhull{E,T}$. Determine conditions that guarentee that the angle of $X$ and $Y$ for $Z$ and $T$ coincide. Suggested solution.
Let's retain the conditions of exam, i.e. $Z$ moves with respect to $T$ in direction $E$ with speed $v$. But this time we look at the rest space of $Z$. Let $W\in Z^\perp$ be a unit vector, such that $T=\b(Z-vW)$, i.e. $T$ moves with respect to $Z$ in direction $-W$. By exam we know that $$ W=\b(vT+E)~. $$ We calculate the projection $X^\prime$ of $X$ on $Z^\perp=\lhull{W,F}$ - so $X^\prime$ is the momentum of $X$ with respect to $Z$: $$ \la X,W\ra=\b(e-v), \la X,F\ra=f \quad\mbox{i.e.}\quad X^\prime=\b(e-v)W+fF~. $$ Putting $f=\sin t$ and $e=\cos t$, we realize that as the momentum of $X$ describes a circle for $T$ $X^\prime$ describes an ellipse centered at $-\b vW$ and its main axes are $\b W$ and $F$ - this is called the relativistic ellipse. All vectors on this ellipse lying in the interior of the unit circle centerd at $0$ are red-shifted and the vectors lying outside are blue-shifted.
light cone
Verify that $0$ is one of the focal points of the ellipse described by $X^\prime$. Suggested solution.
Finally the energy of $X$ with respect to $Z$ is given by $$ -\la X,Z\ra=\b(1-ve)=\b(1-v\cos t)~. $$ For $t=0$ we get $X^\prime=\b(1-v)W$ and $X=T+E$ and for this ray $Z$ measures the lowerst energy, which is not at all surprising!

Perceiving/detecting shapes and colors

Again, we assume that $Z$ is an instantaneous observer, who moves with speed $v$ in the direction $E$ with respect to another instantaneous observer $T$, i.e. $Z\colon=\b(T+vE)$ and $\b=1/\sqrt{1-v^2}$. Put $W\colon=\b(vT+E)$ for some $v\in[0,1)$, then $-vW$ is the velocity of $T$ with respect to $Z$ (cf. exam) and take any light-like vector $$ X=T+eE+fF+gG=T+Y \quad\mbox{i.e.}\quad e^2+f^2+g^2=1~. $$ So $Y$ is any normed vector in the rest space of $T$. We want to determine the normed orthogonal projection $Y^\prime$ of $X$ on the local rest space $Z^\perp=\lhull{W,F,G}$, i.e. we want to determine the direction of $X$ for $Z$. This way the mapping $Y\mapsto Y^\prime$ is a mapping from the Euclidean unit sphere of $T^\perp$ to the Euclidean unit sphere of $Z^\perp$. Denote by $P$ the orthogonal projection onto the local time axis of $Z$ (the momentum of $X$ for $Z$), then the components of $P$ with respect to the orthonormal basis $W,F,G$ of $Z^\perp$ are given by: $$ \la X,W\ra=\b(-v+e),\quad \la X,F\ra=f \quad\mbox{and}\quad \la X,G\ra=g~. $$ Since $\la P,P\ra=\b^2(-v+e)^2+f^2+g^2=\b^2(-v+e)^2+1-e^2=\b^2(1-ev)^2$, we get: $$ Y^\prime=\frac{P}{\Vert P\Vert} =\frac{e-v}{1-ev}W+\frac{f}{\b(1-ev)}F+\frac{g}{\b(1-ev)}G $$ which is exactly the velocity of $X$ with respect to $Z$ - that's not a surprise: $X$ is light-like and thus we know that the norm of its momentum with respect to $Z$ coincides with its energy with respect to $Z$ (cf. e.g. exam, i.e.: $\Vert P\Vert=-\la X,Z\ra=\b(1-ev)$. Thus we get a mapping $S^2\mapsto S^2$ given by: \begin{equation}\label{pereq2}\tag{PER2} (e,f,g)\mapsto\frac{(e-v,\sqrt{1-v^2}f,\sqrt{1-v^2}g)}{1-ev} \end{equation} We will see shortly (cf. section) that this mapping is well known in conformal geometry: it's a Möbius mapping up to a sign.
Always keep in mind that this map $S^2\mapsto S^2$ is obtained by identifying the rest spaces $T^\perp=\lhull{E,F,G}$ and $Z^\perp=\lhull{W,F,G}$. Hence another way to arrive at \eqref{pereq2} is as follows: we perform a boost $u$, defined by $u:T\mapsto\b(T+vE)$, $u:E\mapsto\b(vT+E)$ and $u(F)=F$, $u(G)=G$. Its inverse maps $T$ onto $\b(T-vE)$ and $E$ onto $\b(-vT+E)$. The light-like vector $X=T+eE+fF+gG$ will be mapped by $u^{-1}$ onto $$ \b(T-vE)+e\b(-vT+E)+fF+gG=\b(1-ev)T+\b(e-v)E+fF+gG $$ and its orthogonal projection to the rest space of $T$ is: $\b(e-v)E+fF+gG$. Normalizing gives the required result.
Anyhow, now we know how to transform the 'directions', but what's about the energies? Well, the energy of $X$ with respect to $Z$ is just by definition $$ -\la X,Z\ra=\b(1-ev)~. $$
If $e^2v-2e+v > 0$ then $Z$ experiences a blue shift, otherwise $Z$ experiences a red shift.
Determine those light-like $X$, which have the same energy for $Z$ and $T$. Verify that for small speed $v$ this happens if $e\sim v/2$.
If the firmament observed by an instantaneous observer $T$ is populated by uniformly distributed lime colored stars, then a moving instantaneous observer $Z$ will see a multi colored distribution of stars concentrated at about $W$ and not $-W$ - that's because incident rays are inverted, left/right and up/down are interchanged: e.g. light from 'the right' will point to 'the left'.
Let's assume that our detector is some sort of camera obscura with a hemispherical projection surface and an opening in the center of the sphere, then a circle in front of the instantaneous observer $T$ will be mapped to an ellipse as in the picture below - the circle and the ellipse in the picture are projected to $\lhull{E,G}$ and $\lhull{W,G}$, respectively.
light cone
However, we actually see this circle not shifted to the left but to the right due to some neurological processes in our brain. Here we usually ignore this inversion conducted by our brain because it's physically irrelevant!

Conformal Transformations

Relativistic perception and Möbius transformations

In the previous section we found a mapping which maps the direction $Y\colon=eE+fF+gG$ of a ray of light for an instantaneous observer $T$ to the direction $$ Y^\prime\colon=\frac{e-v}{1-ev}W+\frac{f}{\b(1-ev)}F+\frac{g}{\b(1-ev)}G \quad\mbox{where}\quad W\colon=\b(vT+E), $$ observed by an instantaneous observer $Z$, who moves with respect to $T$ with speed $v$ in the direction $E$. Since we want to compare both observers visual perceptions, we need some way to identify the instantaneous observers rest spaces: The identification of the rest space $\lhull{E,F,G}$ of $T$ and the rest space $\lhull{W,F,G}$ of $Z$ will be achieved via a boost, which maps $Z$ onto $T$, $W$ onto $E$ and $F$ and $G$ onto themselves - that's again the inverse of the boost $u$ alluded to in the previous subsection! Thus we get a mapping $Y\mapsto Y^\dprime$ from $S^2$ into itself (first map $Y$ to $Y^\prime$ and then apply our boost), in coordinates this amounts to $$ (e,f,g)\mapsto\frac{(e-v,\sqrt{1-v^2}f,\sqrt{1-v^2}g)}{1-ev}~. $$ We now turn to another geometric, i.e. coordinate free description of this map: let $P_V$ denote the orthogonal projection to the one dimensional subspace generated by $V=vE$ in the Euclidean space $\lhull{E,F,G}$, i.e. $$ P_V(Y)=\la Y,V\ra V/v^2=eE $$ and denote by $Q_V$ the orthogonal projection to its orthogonal complement $\lhull{F,G}$, i.e. $$ Q_V(Y)\colon=Y-P_V(Y)=fF+gG $$ Then for any $Y=eE+fF+gG\in S^2$ the mapping $Y\mapsto Y^\dprime$ is given by $$ Y^\dprime=-\frac{V-P_V(Y)-\sqrt{1-\Vert V\Vert^2}Q_V(Y)}{1-\la Y,V\ra}~. $$ and the energy of $X=T+Y$ with respect to $Z$ is $-\la X,Z\ra=\b(1-\la Y,V\ra)$. Up to the sign the mapping $Y\mapsto Y^\dprime$ is just the definition of a Möbius map $S^2\rar S^2$. Moreover this can be extended to material particles $X=\g(T+Y)$, $\Vert Y\Vert < 1$:
Suppose we have a (four dimensional) Lorentz space; let $T,Z,X$ be instantaneous observers: $X=\g(T+Y)$, $Z=\b(T+vE)$ for $Y,E\in T^\perp$, $\Vert Y\Vert,v < 1$, $\Vert E\Vert=1$ and $\norm Y < 1$. Then the velocity of $X$ with respect to $Z$ is given by definition by $$ Y^\prime=\frac{X+\la X,Z\ra Z}{-\la X,Z\ra}~. $$ Let $u$ be the boost $T\to Z$, $E\to W\colon=\b(vT+E)\to E$, $u|\lhull{T,E}^\perp=id$. Then $Y\mapsto-Y^\dprime\colon=-u^{-1}(Y^\prime)$ is a transformation on $B^3\colon=\{\Vert Y\Vert < 1\}$, which extends the Möbius transformation $S^2\rar S^2$. Suggested solution.
We will shortly verify that Möbius transformations $B^3\rar B^3$ and its restrictions $S^2\rar S^2$ are onto (cf. proposition). Pertaining observations this means that any instantaneous observer observes something in any direction - well, that's what everyone would probably expect. But let us look at the ultra-relativistic case $\Vert V\Vert\uar1$: the image of $Y\mapsto Y^\prime$ concentrates almost all directions $Y$ at a single point: $-W$. Hence for an ultra-relativistic observer $Z$ almost all directions will be mapped at about a single point and $Z$ experiences a blue shift for these directions. On the other hand only a small fraction of directions about $E$ gets blown up to fill almost all of the sphere and these directions will be red shifted for $Z$. Thus for $Z$ almost all of the universe concentrates in a light ray of very high energy in the direction of motion of $T$.

Classical aberration

Classically aberration is explained as the difference of velocities of light for different observers: if $p$ is the velocity of a ray of light for an observer who is at rest (in the classical sense) for the source of light, then $p-vz$ is the velocity of the ray for an observer who moves in the direction $z\in S^2$ with speed $v$. Hence if $x\colon=p/\Vert p\Vert\in S^2$ is the direction of the ray for the observer at rest, then $y\colon=(p-vz)/\Vert p-vz\Vert\in S^2$ is the direction for the second observer. Assuming, as we do, that the speed of light is $1$ and $|v| < 1$, we get a map $F_c:S^2\rar S^2$, $$ F_c(x)\colon=\frac{x-vz}{\Vert x-vz\Vert} $$ which we call the classical aberration map.

Möbius transformations on $B^n$ and $S^{n-1}$

The remainder of this chapter is purely Euclidean. Hence we return to the Euclidean space $\R^n$ and lowercase letters for vectors! Let $a$ be any vector in the open unit ball $B^n=[\Vert.\Vert < 1]$ and put $S^{n-1}\colon=\pa B^n=[\Vert.\Vert=1]$, $$ P_a(x)\colon=\frac{\la x,a\ra a}{\Vert a\Vert^2} \quad\mbox{and}\quad Q_a(x)\colon=x-P_a(x), $$ i.e. $P_a$ is the orthogonal projection onto the space $\lhull{a}$ generated by $a$ and $Q_a$ is the orthogonal projection onto $\lhull{a}^\perp$. Then the Möbius transformation $M_a$ is defined for all $x\in\R^n$ satisfying $\la a,x\ra\neq1$: \begin{equation}\label{ctreq1}\tag{CTR1} M_a(x)\colon=\frac{a-P_a(x)-\sqrt{1-\Vert a\Vert^2}Q_a(x)}{1-\la x,a\ra} \end{equation}
The following assertions hold:
  1. $M_a(a)=0$ and $M_a(0)=a$.
  2. $M_a:B^n\rar B^n$ and $M_a:S^{n-1}\rar S^{n-1}$, more precisely: $$ \Vert M_a(x)\Vert^2 =1-\frac{(1-\Vert x\Vert^2)(1-\Vert a\Vert^2)}{(1-\la a,x\ra)^2}~. $$
  3. If $U:\R^n\rar\R^n$ is a linear isometry, then $P_a\circ U=U\circ P_{U^*(a)}$ and therefore: $M_a\circ U=U\circ M_{U^*(a)}$.
  4. $M_a$ is an involution, i.e. $M_a\circ M_a=id$.
  5. The derivative of $M_a$ at $x$ and its determinant are given by \begin{eqnarray*} DM_a(x) &=&\frac{\la a,.\ra M_a(x)-P_a-\sqrt{1-\Vert a\Vert^2}Q_a}{1-\la x,a\ra}\\ \det DM_a(x) &=&(-1)^{n}\Bigg(\frac{\sqrt{1-\Vert a\Vert^2}}{1-\la x,a\ra}\Bigg)^{n+1}~. \end{eqnarray*}
  6. Suppose $x\in S^{n-1}$, then the modulus of the determinant of the linear mapping $DM_a(x):x^\perp\rar M_a(x)^\perp$ is $$ \Bigg(\frac{\sqrt{1-\Vert a\Vert^2}}{1-\la x,a\ra}\Bigg)^{n-1} $$ Remark: The determinant is the determinant of the matrix with respect to orthonormal bases of $x^\perp$ and $M_a(x)^\perp$, respectively!
$\proof$ 2. Since $\norm{P_a(x)}^2+\norm{Q_a(x)}^2=\Vert x\Vert^2$ and $\la P_a(x),a\ra=\la a,x\ra$, it follows that: \begin{eqnarray*} \norm{M_a(x)}^2(1-\la a,x\ra)^2 &=&\norm{a-P_a(x)}^2+(1-\Vert a\Vert^2)\norm{Q_a(x)}^2\\ &=&\Vert a\Vert^2-2\la P_a(x),a\ra+\norm{P_a(x)}^2+\norm{Q_a(x)}^2 -\Vert a\Vert^2\norm{Q_a(x)}^2\\ &=&\Vert a\Vert^2-2\la P_a(x),a\ra+\Vert x\Vert^2 -\Vert a\Vert^2(\Vert x\Vert^2-\norm{P_a(x)}^2)\\ &=&\Vert a\Vert^2-2\la x,a\ra+\Vert x\Vert^2 -\Vert a\Vert^2\Vert x\Vert^2+\la x,a\ra^2\\ &=&(1-\la a,x\ra)^2-(1-\Vert x\Vert^2)(1-\Vert a\Vert^2)~. \end{eqnarray*} 3. $U$ is an isometry, hence $U^{-1}=U^*$ and $\Vert a\Vert=\Vert U^*a\Vert$. We also have $P_aU=UP_{U^*a}$ and $Q_aU=UQ_{U^*a}$, because for all $x\in\R^n$: $$ P_aUx =\frac{\la Ux,a\ra a}{\Vert a\Vert^2} =\frac{\la x,U^*a\ra a}{\Vert a\Vert^2} =\frac{\la x,U^*a\ra UU^*a}{\Vert U^*a\Vert^2} =UP_{U^*a}x~. $$ Thus we conclude that \begin{eqnarray*} M_a(Ux) &=&\frac{a-P_a(Ux)-\sqrt{1-\Vert a\Vert^2}\,Q_a(Ux)}{1-\la Ux,a\ra}\\ &=&U\frac{U^*a-P_{U^*a}-\sqrt{1-\norm{U^*a}^2}\,Q_{U^*a}x)}{1-\la x,U^*a\ra} =UM_{U^*a}(x)~. \end{eqnarray*} 4. By definition we get: \begin{eqnarray*} P_a(M_a(x))&=&\frac{a-P_a(x)}{1-\la a,x\ra}\\ Q_a(M_a(x))&=&-\frac{\sqrt{1-\Vert a\Vert^2}\,Q_a(x)}{1-\la a,x\ra}\quad\mbox{and}\\ \la M_a(x),a\ra&=&\la P_a(M_a(x)),a\ra=\frac{\Vert a\Vert^2-\la x,a\ra}{1-\la x,a\ra} \end{eqnarray*} and therefore \begin{eqnarray*} M_a(M_a(x))&=&\frac{a-P_a(M_a(x))-\sqrt{1-\Vert a\Vert^2}\,Q_a(M_a(x))}{1-\la M_a(x),a\ra}\\ &=&\frac{a-\frac{a-P_a(x)}{1-\la a,x\ra} +\frac{(1-\Vert a\Vert^2)Q_a(x)}{1-\la a,x\ra}} {1-\frac{\Vert a\Vert^2-\la x,a\ra}{1-\la x,a\ra}}\\ &=&\frac{a(1-\la a,x\ra)-a+P_a(x)+(1-\Vert a\Vert^2)Q_a(x)} {1-\la x,a\ra-\Vert a\Vert^2+\la x,a\ra}\\ &=&\frac{-P_a(x)\Vert a\Vert^2+P_a(x)+(1-\Vert a\Vert^2)Q_a(x)} {1-\Vert a\Vert^2}=x \end{eqnarray*} 5. Since both $P_a$ and $Q_a$ are linear, we get by the product (or quotient) rule: $$ DM_a(x)v =\frac{\la v,a\ra M_a(x)-P_a(v)-\sqrt{1-\Vert a\Vert^2}\,Q_a(v)}{1-\la x,a\ra} $$ Let $e_1\colon=a/\Vert a\Vert,e_2,\ldots,e_n$ be an orthonormal basis and put $$ Av\colon=\la v,a\ra M_a(x)-P_a(v)-\sqrt{1-\Vert a\Vert^2}\,Q_a(v), $$ then $Ae_1=\Vert a\Vert M_a(x)-a/\Vert a\Vert$ and for $j\geq2$: $Ae_j=-(1-\Vert a\Vert^2)^{1/2}e_j$. Hence we conclude that $$ \det A=(-1)^{n-1}(1-\Vert a\Vert^2)^{(n-1)/2}\la Ae_1,e_1\ra~. $$ Finally $$ \la Ae_1,e_1\ra =\frac{\la\Vert a\Vert M_a(x)-\frac{a}{\Vert a\Vert},a\ra}{\Vert a\Vert} =\la M_a(x),a\ra-1 $$ and since $\la M_a(x),a\ra=\la a-x,a\ra/(1-\la x,a\ra)$ we conclude that $$ \la Ae_1,e_1\ra=-\frac{1-\Vert a\Vert^2}{1-\la x,a\ra}~. $$ 6. By 2. $DM_a(x)$ maps $x^\perp$ into $M_a(x)^\perp$; hence the determinant of this map is the determinant of $DM_a(x):\R^n\rar\R^n$ devided by the component of the normal derivative along $M_a(x)$. The derivative in the direction of the normal is $DM_a(x)x$ and the component thereof in the direction of the normal at $M_a(x)$ is $\la DM_a(x),M_a(x)\ra$, which is just half of the derivative of $\la M_a(x),M_a(x)\ra$ in direction $x$. By 2. we have $$ 1-\norm{M_a(x)}^2 =\frac{(1-\Vert a\Vert^2)(1-\Vert x\Vert^2)}{(1-\la x,a\ra)^2} $$ which readily implies that the derivative of $\la M_a(x),M_a(x)\ra$ in direction $x\in S^{n-1}$ is given by: $2(1-\Vert a\Vert^2)/(1-\la x,a\ra)^{2}$. $\eofproof$
Show that for all $x\in B^n$: $$ DM_a(x)x =\frac{M_a(x)-a}{1-\la x,a\ra}~. $$ Conclude that for all $x\in S^{n-1}$: $$ \la DM_a(x)x,M_a(x)\ra =\frac{1-\Vert a\Vert^2}{(1-\la x,a\ra)^2}~. $$
Verify that $M_a(-x)=-M_{-a}(x)$.
The adjoint of $Ux\colon=-x$ is $U$ and thus the result follows by proposition.
Verify that the inverse of $L_a:x\mapsto-M_a(x)$ is given by $x\mapsto L_{-a}(x)$.
Put $y\colon=M_{-a}x$, then $L_{a}(L_{-a}x)=-M_a(-M_{-a}x)=-M_a(-y)=M_{-a}y=M_{-a}M_{-a}x=x$ and interchanging $a$ and $-a$, the result follows.
For all non negative measurable functions $f:B^n\rar[0,\infty]$ (suggested solution): $$ \int_{B^n} f(M_a(x))\,dx =\int_{B^n} f(x)\Bigg(\frac{\sqrt{1-\Vert a\Vert^2}}{1-\la x,a\ra}\Bigg)^{n+1}\,dx~. $$ In other words: the image measure of the Lebesgue measure on $B^n$ under the mapping $M_a$ has density $$ \r(x)\colon=\Bigg(\frac{\sqrt{1-\Vert a\Vert^2}}{1-\la x,a\ra}\Bigg)^{n+1}~. $$

Conformal mappings

Suppose $M,N$ are open subsets of Euclidean space $\R^n$ endowed with the canonical Euclidean metric (cf. subsection). We will identify the tangent space $T_xM$ (and $T_yN$) at any point $x\in M$ (and $y\in N$) with the Euclidean space $\R^n$ (cf. subsection). A smooth mapping $F:M\rar N$ is conformal if there exists some smooth scaling function $h:M\rar\R^+$, such that $$ \forall x\in M\,\forall u\in\R^n:\quad \la DF(x)u,DF(x)u\ra=h(x)^2\Vert u\Vert^2, $$ where $\la.,.\ra$ denotes the canonical Euclidean product on $\R^n$. This is equivalent to the fact that the linear mapping $DF(x)^*DF(x)$ is just multiplication by the factor $h(x)^2$. This definition obviously extends to Riemannian manifolds $(M,\la.,.\ra)$ and $(N,g)$ and smooth mappings $F:M\rar N$: $F$ is said to be conformal if for all $x\in M$ and all vector fields $X$ on $M$: \begin{equation}\label{ctreq2}\tag{CTR2} g(T_xF(X_x),T_xF(X_x)) =h(x)^2\la X_x,X_x\ra, \end{equation} in other words: the pull-back metric of $g$ by $F$ is $h^2\la.,.\ra$. We will only need the cases where $M$ and $N$ are either $S^n$ or open subsets of the Euclidean space $\R^n$. What about the scaling function $h$? It will tell you the local magnification: a tangent vector $u$ at $x$ is mapped onto the tangent vector $DF(x)u$ at $F(x)$ and $$ \Vert DF(x)u\Vert=h(x)\Vert u\Vert~. $$ Thus distances at about $x$ get blown up by the factor $h(x)$.
The inversion $I:M\rar M$, $x\mapsto x/\Vert x\Vert^2$ is conformal on $M\colon=\R^n\sm\{0\}$ with scaling function $h(x)=1/\Vert x\Vert^2$. Hint: $DI(x)v=(v-2x\la x,v\ra/\Vert x\Vert^2)/\Vert x\Vert^2$. Suggested solution.
$F(r,\vp,\theta)=(r\cos\vp\cos\theta,r\sin\vp\cos\theta,r\sin\theta)$ is not a conformal mapping from $\R^+\times(-\pi,\pi)\times(-\pi/2,\pi/2)$ into $\R^3$. Suggested solution.
Prove that a linear map $A:\R^n\rar\R^n$ is conformal iff there exists some $r > 0$ such that $rA$ is an isometry.
The composition of conformal mappings is conformal. Suggested solution
Suppose $M,N$ are open subsets of $\R^n$. A smooth map $F:M\rar N$ is conformal iff (suggested solution) $$ \forall x\in M\,\forall u,v\in\R^n:\quad \la DF(x)u,DF(x)v\ra=h(x)^2\la u,v\ra $$
This example evidently shows that conformal mappings are angle preserving (the converse is also true - cf. exam), meaning that for any $x\in M$ and any pair of smooth curves $c_1,c_2:(-\e,\e)\rar M$ such that $c_1(0)=c_2(0)=x$, the angles of $c_1^\prime(0)$ and $c_2^\prime(0)$ and $(F\circ c_1)^\prime(0)$ and $(F\circ c_2)^\prime(0)$ coincide. By the chain rule and the definition of the angle this comes down to $$ \frac{\la c_1^\prime(0),c_2^\prime(0)\ra}{\Vert c_1^\prime(0)\Vert\Vert c_2^\prime(0)\Vert} =\frac{\la DF(x)c_1^\prime(0),DF(x)c_2^\prime(0)\ra}{\Vert DF(x)c_1^\prime(0)\Vert\Vert DF(x)c_2^\prime(0)\Vert} $$ and by the previous example this obviously holds if $F$ is conformal.
If we want to check conformity of $M_a$ we have to compute $DM_a(x)^*DM_a(x)$. Of course, we may assume that $a=(v,0,\ldots,0)$ and therefore the map $-M_a$ is given in Euclidean coordinates $x=(x_1,\ldots,x_n)\in\R^n$ by - compare \eqref{pereq2}: $$ (x_1,\ldots,x_n)\mapsto\Big(\frac{x_1-v}{1-x_1v},\frac{\sqrt{1-v^2}x_2}{1-x_1v},\ldots,\frac{\sqrt{1-v^2}x_n}{1-x_1v}\Big) $$ and the Jacobi matrix of this map is: $$ \left(\begin{array}{ccccc} \frac{1-v^2}{(1-x_1v)^2}&0&0&\cdots&0\\ \frac{v\sqrt{1-v^2}x_2}{(1-x_1v)^2}&\frac{\sqrt{1-v^2}}{1-x_1v}&0&\cdots&0\\ \frac{v\sqrt{1-v^2}x_3}{(1-x_1v)^2}&0&\frac{\sqrt{1-v^2}}{1-x_1v}&\cdots&0\\ \vdots&\ddots&\ddots&\ddots&\vdots\\ \frac{v\sqrt{1-v^2}x_n}{(1-x_1v)^2}&0&0&\cdots&\frac{\sqrt{1-v^2}}{1-x_1v} \end{array}\right) $$ For simplicity let's assume $n=3$. Then we get for the matrix of $DM_a(x)^*DM_a(x)$: $$ \frac{(1-v^2)}{(1-x_1v)^2} \left(\begin{array}{ccc} \frac{v^2(x_2^2+x_3^2)+(1-v^2)}{(1-x_1v)^2}&\frac{vx_2}{1-x_1v}&\frac{vx_3}{1-x_1v}\\ \frac{vx_2}{1-x_1v}&1&0\\ \frac{vx_3}{1-x_1v}&0&1 \end{array}\right)~. $$ This obviously shows that $-M_a$ and thus $M_a$ is not conformal on $B^3$, but may be its restriction to $S^2$ is conformal, i.e. $$ \forall x\in S^2\forall u\perp x:\quad \la DM_a(x)^*DM_a(x)u,u\ra=h(x)^2\Vert u\Vert^2~. $$ Suppose $x\in S^2$ and $u$ is in the tangent space $T_xS^2$ of $S^2$ at $x$ i.e. $\la u,x\ra=0$, dropping the common factor $(1-v^2)/(1-x_1v)^2$ we get for the matrix of $DM_a(x)^*DM_a(x)$: $$ \left(\begin{array}{ccc} \frac{1-v^2x_1^2}{(1-x_1v)^2}&\frac{vx_2}{1-x_1v}&\frac{vx_3}{1-x_1v}\\ \frac{vx_2}{1-x_1v}&1&0\\ \frac{vx_3}{1-x_1v}&0&1 \end{array}\right) $$ Employing $x_2u_2+x_3u_3=-x_1u_1$ we see that $\la DM_a(x)^*DM_a(x)u,u\ra$ is given by \begin{eqnarray*} &&\frac{1-v^2x_1^2}{(1-x_1v)^2}u_1^2+u_2^2+u_3^2 +2\frac{vx_2}{1-x_1v}u_1u_2+\frac{vx_3}{1-x_1v}u_1u_3\\ &=&\Big(\frac{1-v^2x_1^2}{(1-x_1v)^2}-2\frac{x_1v}{1-x_1v}x_1\Big)u_1^2+u_2^2+u_3^2\\ &=&\frac{1-v^2x_1^2-2x_1v(1-x_1v)}{(1-x_1v)^2}u_1^2+u_2^2+u_3^2=\Vert u\Vert^2~. \end{eqnarray*} These calculations obviously extend to spheres of arbitrary dimension:
Every Möbius transformation $M_a:S^{n-1}\rar S^{n-1}$ is conformal with scaling function $$ h(x)=\frac{\sqrt{1-\Vert a\Vert^2}}{1-\la x,a\ra}; $$ and thus $$ \sqrt{\frac{1-\Vert a\Vert}{1+\Vert a\Vert}} \leq h(x) \leq\sqrt{\frac{1+\Vert a\Vert}{1-\Vert a\Vert}}~. $$ Moreover $-M_a$ can be described as follws: put $v=\Vert a\Vert$ and $e=a/v$. Take any vector $x\in S^{n-1}$, form the light-like vector $y\colon=e_0+x$ in Minkowski space $\R_1^{n+1}$, apply a boost with speed $v$ in the direction $-e$, project the resulting vector orthogonally on $e_0^\perp\simeq\R^n$ and normalize to get $-M_a(x)$.
Hence the view of an instantaneous observer may be distorted, but the distortion is not that bad: it preserves angles! A geometric object like a rectangle will be seen as an object with four vertices and the angles at these corners will still be 90 degrees. The following depicts the image of an orthogonal grid formed by lines of constant latitude or longitude of $S^2$ under a Möbius transformation for $v=0,1/4,3/4,0.95$ with untrue colors.
light cone light cone
light cone light cone
Use proposition to verify that for all $x\in S^{n-1}$ and all $u\in\R^n$ such that $u\perp x$: $$ \norm{DM_a(x)u}=\frac{\sqrt{1-\Vert a\Vert^2}}{1-\la x,a\ra}\Vert u\Vert~. $$
Suppose $|v| < 1$ and $\Vert z\Vert=1$. Is the classical aberration map $F_c:S^{n-1}\rar S^{n-1}$, $$ x\mapsto\frac{x-vz}{\Vert x-vz\Vert} $$ a conformal transformation of $S^{n-1}$? 2. Compute the inverse of $F_c$. Suggested solution
Classical versus relativistic aberration for $v=0.9$, again with untrue colors:
classic relativistic
Show that every smooth isometry $F:S^{n-1}\rar S^{n-1}$ is the restriction of a linear isometry $U$ of the Euclidean space $\R^n$.
Every conformal mapping $F:S^n\rar S^n$, $n\geq3$, is the composition of Möbius transformations and isometries.
Suppose $M,N$ are open subsets of $\R^n$. A smooth map $F:M\rar N$ is conformal if and only if it preserves angles. Suggested solution.
This file contains coastline data in spherical coordinates: longitude and latitude in degrees! Write a program that applies a Möbius map to these points and produces pairs of spherical coordinates (longitude and latitude) in degrees on output.
coastline00 coastline09
The picture on the right is the image of the left hand side (the grid of lines of constant latitude or longitude is not transformed) under a Möbius transformation, which corresponds to an instantaneous observer moving from the center towards the north pole with speed $v=0.95$.

A model of an eye

The human eye simplified is a camera obscura with a spherical projection surface $S^2$ (the retina) and an opening (the pupil of the eye), which we locate in the north pol $N$ of $S^2$. Any point on the line joining the north pol with a point $x$ on the sphere will be seen as one point. Now we place in front of the camera a plane picture and determine its image on the sphere. For convenience of calculation we move the plane to the center of the sphere.
model of an eye
Identifying this plane with $\R^2$ we get a map $\vp_N^{-1}:\R^2\rar S^2(\sbe\R^3)$; we study its inverse $\vp_N:S^2\sm\{N\}\rar\R^2$. Denoting the coordinates of $x$ and $y$ by $(x_1,x_2,x_3)$ and $(y_1,y_2)$ respectively we get by the intercept theorem: $x_1:y_1=(1-x_3):1$, i.e.: $$ y=\vp_N(x)=\frac{(x_1,x_2)}{1-x_3}~. $$ This map $\vp_N$ is called the stereographic projection. There is one important property it has in common with Möbius transformations: it is conformal. Since $\vp_N$ is defined on the open subset $[x_{n+1}\neq1]$ of $\R^{n+1}$ this means that for all $x\in S^n\sm\{N\}$ and all $u$ in the tangent space $T_xS^n$ of $S^n$ at $x$, i.e. $\la u,x\ra=0$, we have $$ \la D\vp_N(x)^*D\vp_N(x)u,u\ra=h(x)^2\Vert u\Vert^2~. $$
Let $\vp_N:S^n\sm\{N\}\rar\R^n$ be the stereographic projection - $N$ being the north pol, i.e. $N=(0,\ldots,0,1)\in\R^{n+1}$: $$ \vp_N(x)=\frac{(x_1,\ldots,x_n)}{1-x_{n+1}}~. $$ Then $\vp_N$ is conformal with scaling function $h(x)=(1-x_{n+1})^{-1}$.
$\proof$ The case $n=2$ suffices. The matrices of $D\vp_N(x)$ and $D\vp_N(x)^*D\vp_N(x)$ are given by: $$ \frac1{1-x_3} \left(\begin{array}{ccc} 1&0&\frac{x_1}{1-x_3}\\ 0&1&\frac{x_2}{1-x_3} \end{array}\right) \quad\mbox{and}\quad \frac1{(1-x_3)^2} \left(\begin{array}{ccc} 1&0&\frac{x_1}{1-x_3}\\ 0&1&\frac{x_2}{1-x_3}\\ \frac{x_1}{1-x_3}&\frac{x_2}{1-x_3}&\frac{x_1^2+x_2^2}{(1-x_3)^2} \end{array}\right) $$ Thus for $x\in S^2$ and $\la u,x\ra=0$ we obtain for $\la D\vp_N(x)^*D\vp_N(x)u,u\ra$ (without the factor $(1-x_3)^{-2}$): \begin{eqnarray*} &&u_1^2+u_2^2 +2\frac{x_1u_1+x_2u_2}{1-x_3}u_3 +\frac{x_1^2+x_2^2}{(1-x_3)^2}u_3^2\\ &=&u_1^2+u_2^2 -2\frac{x_3u_3^2}{1-x_3} +\frac{1+x_3}{1-x_3}u_3^2\\ &=&u_1^2+u_2^2 +\frac{1-x_3}{1-x_3}u_3^2 =\la u,u\ra \end{eqnarray*} $\eofproof$
So our camera obscura produces a spherical image from a flat image by inverting a stereographic projection. Hence this spherical image is conformal to the flat image!
Let $\vp_S:S^n\sm\{S\}\rar\R^n$ be the stereographic projection - $S$ being the south pol, i.e. $S=(0,\ldots,0,-1)\in\R^{n+1}$: $$ \vp_S(x)=\frac{(x_1,\ldots,x_n)}{1+x_{n+1}}~. $$ Show that $\vp_N\circ\vp_S^{-1}$ is the inversion. Again, this shows that the inversion is a conformal map of $\R^n\sm\{0\}$!
We just need to draw a picture and notice similarity of triangles: $\norm{\vp_N(x)}:1=1:\norm{\vp_S(x)}$.
stereographic projection
Show that $\vp_N^{-1}:\R^n\rar S^n$ is given by
$$ \forall y\in\R^n:\quad \vp_N^{-1}(y) =\frac1{1+\Vert y\Vert^2}(2y_1,\ldots,2y_n,\Vert y\Vert^2-1)~. $$
Prove that the mapping $\psi(x)=x/x_{n+1}$ maps the hemisphere $H\colon=S^n\cap[x_{n+1} < 0]$ onto $\R^n$. Is $\psi:H\rar\R^n$ conformal? Determine the inverse of $\psi$. Suggested solution.
Prove that the map $F:(-\pi,\pi)\times(-\pi/2,\pi/2)\rar S^2$, $$ F(\vp,\theta)\colon=(\cos\theta\cos\vp,\cos\theta\sin\vp,\sin\theta) $$ is not conformal - the set $(-\pi,\pi)\times(-\pi/2,\pi/2)$ carries the canonical Euclidean metric. Find a Riemannian metric $g$ on $(-\pi,\pi)\times(-\pi/2,\pi/2)$ such that $F$ is a local isometry.
Prove that the Mercator map $F:S^2\sm\{S,N\}\rar S^1\times\R$, $F(\vp,\theta)\colon=(\vp,\tan\theta)$ is conformal. You may resort to the Riemannan metric $g$ of exam or may use the fact that $F$ is the restriction of the map $F:\R^3\sm\{(0,0,\R)\}\rar\R^3$: $$ (x_1,x_2,x_3)\mapsto\frac{(x_1,x_2,x_3)}{\sqrt{x_1^2+x_2^2}} $$ to the sphere $S^2$. The Mercator map is also called cylindrical projection and has been rampant in navigation.

Conformal mappings and complex analysis

We conclude this chapter by stating two results from complex analysis: Every conformal map $F:M\rar\R^2$ on an open subset $M$ of $\R^2$ satisfying $\det DF(x,y) > 0$ is holomorphic, i.e. $F$ as a mapping from the open subset $M$ of $\C$ in $\C$ is complex differentiable. For the real map $F:M\rar\R^2$, $(x,y)\mapsto(u(x),v(y))$ this means that $F$ is differentiable in the real sense and the so called Cauchy-Riemann equations hold: $$ \pa_xu=\pa_yv \quad\mbox{and}\quad \pa_yu=-\pa_xv~. $$ Now it's easily checked that any holomorphic function $F:M\rar\C$ on an open subset $M$ of $\C$ is conformal as a mapping from the open subset $M$ of $\R^2$ into $\R^2$. Indeed, the Cauchy-Riemann equations imply for the corresponding real map $(x,y)\mapsto(u(x,y),v(x,y))$ that the scaling function is given by $$ h=\Vert\nabla u\Vert=\Vert\nabla v\Vert\colon=\sqrt{(\pa_xv)^2+(\pa_yv)^2}~. $$ More exactly: according to our definition of conformity a holomorphic function $F:M\rar\C$ is conformal on $M\sm\{z=x+iy: \pa_xu(x,y)=\pa_yu(x,y)=0\}$ - on the excluded set we have $h=0$.
Determine the real map $F$ corresponding to the holomorphic map $z\mapsto\cos z$ and compute the scaling function $h$.
For $z=x+iy$ we get $\cos(z)=\cos(x+iy)=\cos(x)\cos(iy)-\sin(x)\sin(iy)$ and since $\cos(iy)=\cosh(y)$ and $\sin(iy)=i\sinh(y)$ $F$ is given by $$ (x,y)\mapsto(\cos(x)\cosh(y),-\sin(x)\sinh(y))~. $$ It follows that $u(x,y)=\cos(x)\cosh(y)$ and therefore $$ h(x,y)^2 =\Vert\nabla u\Vert^2 =\sin^2(x)\cosh^2(y)+\cos^2(x)\sinh^2(y) =\cosh^2(y)-\cos^2(x), $$ i.e. $F$ is conformal on $\R^2\sm(\pi\Z\times\{0\})$.
The mapping $z\mapsto e^z$ from $\C$ onto $\C\sm\{0\}$ as a real mapping is given by $F:(x,y)\mapsto e^x(\cos y,\sin y)$. Verify by direct calculation that $$ DF(x,y)^*DF(x,y) =e^{2x}\left( \begin{array}{cc} 1&0\\ 0&1 \end{array}\right)~. $$ Thus $F$ is conformal with scaling function $h(x)=e^x$.
Since the map $z\mapsto\bar z$ is conformal (but not holomorphic) and the composition of conformal maps is conformal, we get another class of conformal maps: for every holomorphic function $f$, the map $z\mapsto\cl{f(z)}$ is conformal. These maps are called anti-holomorhpic and the corresponding real function $F(x,y)=(u(x,y),v(x,y))$ satisfies $\pa_xu=-\pa_yv$, $\pa_yu=\pa_xv$ and $\det DF(x,y)=-\Vert\nabla u(x,y)\Vert^2 < 0$.
The composition of two anti-holomorhpic maps is holomorphic and the composition of a holomorphic and an anti-holomorhpic map is anti-holomorhpic.
$F:B^2\rar B^2$ is a holomorphic bijection if and only if $$ F(z)=c\frac{a-z}{1-z\bar a} \quad\mbox{where}\quad |c|=1\quad\mbox{and}\quad a\in B^2~. $$ These maps are called the Möbius transformations on the unit disk $B^2$.
Suppose $a\in[0,1)$. How relates the Möbius transformation $F:S^1\rar S^1$ of the above proposition to the Möbius transformation $M_v:S^1\rar S^1$ described earlier?
Suppose $M$ is a simply connected open subset in $\C$ different from $\C$. Then for any $z_0\in M$ there is a holomorphic (hence conformal) bijection $F:M\rar B^2$ such that $F(z_0)=0$.
The Cayley transform $F(z)\colon=(z-i)/(z+i)$ maps the upper half plane $H^+\colon=[\Im z > 0]$ onto the unit disk $B^2=[|z| < 1]$.
Suppose $w\in H^+$. Then the mapping $F_w(z)\colon=(z-w)/(z-\bar w)$ maps the upper half plane $H^+$ onto the unit disk $B^2$ and $F_w(w)=0$.
The mapping $F:z\mapsto e^{i\pi z}$ maps $S\colon=[0 < \Re z < 1]$ conformaly onto $H^+$. Find for any $w\in S$ a conformal mapping $R_w:S\rar B^2$, which is onto and $R_w(w)=0$. Suggested solution.
Let $D$ be the disk of radius $r < \sqrt{a^2+b^2}$ centered at $a+ib$. Determine the image of $D$ under the map $F(z)\colon=z+1/z$.
If $n\geq2$, then a holomorphic function $f:M\rar\C^n$ on an open subset $M$ of $\C^n$ need not be conformal; even $\C$-linear maps need not be conformal. Actually in $\R^n$, $n\geq3$, there are only a few conformal mappings: the group generated by isometries and the inversion. Thus in dimension two there are loads of conformal mappings, whereas in dimensions greater than two conformal mappings form a very narrow class.
← Inner Products → Tensors
<Home>
Last modified: Tue Oct 29 20:04:37 CET 2024