Exam

The operator $P_{ex}\in\Hom(\C^2\otimes\C^2)$, $P_{ex}:e_j\otimes e_k\mapsto e_k\otimes e_j$, $j,k\in\{1,2\}$, is called the exchange operator (cf. exam). Verify that for all $U\in\Hom(\C^2)$ the operator $U\otimes U$ commutes with $P_{ex}$. Therefore the symmetry group of $P_{ex}$ contains the copy $\{U\otimes U:\,U\in\UU(2)\}$ of $\UU(2)$. Show that $H_0\colon=A(2P_{ex}-1)$ has eigen-values $-3A,A,A,A$. $H_0$ is called the Hamiltonian of a spin $1/2$ couple. The Hamiltonian of this couple in a magnetic field along the third axis is given by: $$ H\colon=H_0+\mu_1B(\s_3\otimes1)+\mu_2B(1\otimes\s_3), $$ where $\s_j$ denote the Pauli spin operators (cf. subsection) and $B,\mu_1,\mu_2\in\R$ the strength of the magnetic field and the magnetic moments of the particles. Compute the eigen-values $E_1,E_2,E_3,E_4$ of $H$.

The first part is included in exam. However we verify $[U\otimes U,P_{ex}]=0$ diretly: On the one hand we have $$ P^{ex}U\otimes U(e_k\otimes e_m) =P^{ex}\sum_{j,l} u_{lk}u_{jm}e_l\otimes e_j =\sum_{j,l}u_{lk}u_{jm}e_j\otimes e_l~, $$ and on the other hand $$ U\otimes U P^{ex}(e_k\otimes e_m) =U\otimes U(e_m\otimes e_k) =\sum_{j,l}u_{jm}u_{lk}e_j\otimes e_l~. 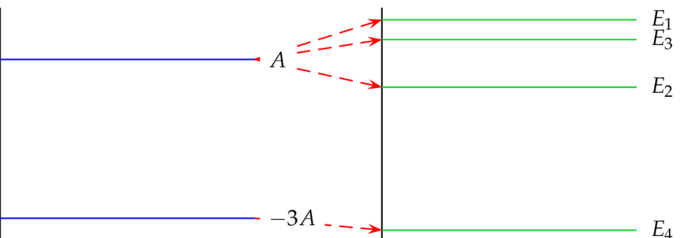$$ The matrices of $H_0$ and $H$ with respect to the basis $e_1\otimes e_1$, $e_1\otimes e_2$, $e_2\otimes e_1$, $e_2\otimes e_2$ are given by $$ \left(\begin{array}{cccc} A&0&0&0\\ 0&-A&2A&0\\ 0&2A&-A&0\\ 0&0&0&A \end{array}\right) \quad\mbox{and}\quad \left(\begin{array}{cccc} A+\mu B&0&0&0\\ 0&-A+\mu^\prime B&2A&0\\ 0&2A&-A-\mu^\prime B&0\\ 0&0&0&A-\mu B \end{array}\right), $$ where $\mu\colon=\mu_1+\mu_2$ and $\mu^\prime\colon=\mu_1-\mu_2$. The eigen-values of $H_0$ are indeed: $-3A,A,A,A$ and the corresponding normalized eigen-vectors are: $(e_2\otimes e_1-e_1\otimes e_2)/\sqrt2$, $(e_2\otimes e_1+e_1\otimes e_2)/\sqrt2$, $e_1\otimes e_1$ und $e_2\otimes e_2$.
The latter two $e_1\otimes e_1$ and $e_2\otimes e_2$ are also eigen-vectors of $H$ with eigen-values: $E_1\colon=A+\mu B$ und $E_2\colon=A-\mu B$. Put $a\colon=B\mu^\prime/2A$, then we obtain for the remaining eigen-values: $E_3=-A+2A\sqrt{1+a^2}$ and $E_4=-A-2A\sqrt{1+a^2}$.