Characters
If $\Psi$ is any finite dimensional unitary representation in $E$, then by proposition $\chi\colon=\tr\Psi$ is the sum of characters, moreover: $\chi(e)=\dim E$, for $\Psi(e)=1_E$ and thus $\tr 1_E=\dim E$. If $\Phi$ is equivalent to $\Psi$, then $\tr\Phi=\tr\Psi$. We will prove later (cf. corollary) that also the converse is true, i.e. two irreducible unitary representations $\Psi_1:G\rar\UU(E_1)$ and $\Psi_2:G\rar\UU(E_2)$ are equivalent iff for all $g\in G$: $\tr\Psi_1(g)=\tr\Psi_2(g)$.
If $\chi$ is a character, then so is $\bar\chi$, because $\bar\chi$ is the trace of the contra-gredient (or dual) representation. Finally, if $\psi$ and $\vp$ are two characters, then their point-wise product $\psi\vp$ is the trace of the tensor product of two representations; since the trace of any representation is a linear combinations of characters with non-negative integer coefficients - such animals are called compound characters, the product of any characters is a compound character.
We will see in a while that all irreducible representations of $G\times H$ are of this form (cf. e.g. exam). Hence the characters of the product of two groups $G$ and $H$ are the tensor products of the characters (remember - cf. exam - for functions $f:X\rar\C$ and $g:Y\rar\C$ we have $f\otimes g:X\times Y\rar\C$: $f\otimes g(x,y)\colon=f(x)g(y)$).
Conjugacy classes
Let $g$ be any element in the group $G$ and put $C(g)\colon=\{hgh^{-1}: h\in G\}$ - this is called the conjugacy class of $g$. We say that $g,g^\prime\in G$ are conjugate, if $g^\prime\in C(g)$.
To get a list of subgroups, with just one subgroup in the set $\{gHg^{-1}:g\in G\}$ and some additional info about these subgroups, you may execute the following commands in sage:
G=AlternatingGroup(4)
SubGroups=G.conjugacy_classes_subgroups()
for Group in SubGroups:
nor=Group.is_normal()
abe=Group.is_abelian()
sim=Group.is_simple()
print(Group,Group.order(),nor,abe,sim)
This will give you the output:
(Subgroup generated by [()], 1, True, True, False)
(Subgroup generated by [(1,2)(3,4)], 2, False, True, True)
(Subgroup generated by [(2,4,3)], 3, False, True, True)
(Subgroup generated by [(1,2)(3,4),(1,3)(2,4)], 4, True, True, False)
(Subgroup generated by [(2,4,3),(1,2)(3,4), (1,3)(2,4)], 12, True, False, False),
Note that permutations are written as compositions of disjoint cycles, i.e. $()$ denotes the identity, $(1,2)(3,4)$ denotes the permutation $(2143)$, $(2,4,3)$ denotes the permutation $(1423)$. Quotient and product groups can also be created easily: Take the alternating group $G=A(4)$, two elements $g_1$ and $g_2$ of this group and the subgroup $H$ generated by these two elements, check if $H$ is normal and construct the quotient group $G/H$; check if $G/H$ is isomorphic to $\Z_3$; finally create the product group $\Z_3\times\Z_3$:
G=AlternatingGroup(4)
g1=G('(1,2)(3,4)')
g2=G('(1,3)(2,4)')
H=G.subgroup([g1,g2])
H.is_normal()
GqH=G.quotient(H)
GqH.is_isomorphic(CyclicPermutationGroup(3))
K=direct_product_permgroups([CyclicPermutationGroup(3),CyclicPermutationGroup(3)])
Now suppose we have a character $\chi\in\wh G$ some $g\in G$ and $g^\prime\in C(g)$, then
$$
\chi(g^\prime)
=\tr\Psi(h^{-1}gh)
=\tr(\Psi(h^{-1})\Psi(g)\Psi(h))
=\tr\Psi(g)
=\chi(g),
$$
i.e. characters are constant on conjugacy classes - functions $f:G\rar\C$ with this property are called class functions (cf. proposition). We will in fact see that the number of characters, which by definition equals the number of pairwise in-equivalent irreducible representations, equals the number of conjugacy classes (cf. theorem). The following is a standard result in group theory - compare Lagrange`s theorem, which states that the order $|H|$ of a subgroup $H$ of a group $G$ divides the order of $G$.
$\proof$
For $g\in G$ put $Z(g)\colon=\{h\in G:gh=hg\}$ - the centralizer of $g$; this is indeed a subgroup of $G$. The mapping $u:G\rar C(g)$, $h\mapsto hgh^{-1}$ is by definition of $C(g)$ onto and $u(h_1)=u(h_2)$ iff $h_2^{-1}h_1gh_1^{-1}h_2=g$, i.e. iff $h_1^{-1}h_2\in Z(g)$. It follows that: $|G|=|Z(g)||C(g)|$.
$\eofproof$
To get the order of all centralizers in sage:
G=SymmetricGroup(5)
Reps=G.conjugacy_classes_representatives()
Sizes=[]
for g in Reps:
Sizes.append(G.centralizer(g).order())
print(Sizes)
Proposition can be generalized in the following sense:
This can be used to determine all finite subgroup $G$ of $\SO(3)$: Remember from section that every $g\in\SO(3)$ has a rotation axis and therefore the action of $\SO(3)$ on $S^2$ fixes a pair of antipodal points of $S^2$. Let $X$ be the set of points that come out as fixed points for some $g\in G\sm\{E\}$. Then $G\cdot X\sbe X$, for if $x\in X$, then there is some $g_x\in G$ such that $g_xx=x$ and for any $g\in G$ we have $(gg_xg^{-1})gx=gx$, i.e. $gx$ is a fixed point of $gg_xg^{-1}\in G$ - this also shows that $S(gx)=gS(x)g^{-1}$. The essential observation is that $S(x)=S(-x)$ and for $y\neq\pm x$: $(S(x)\sm\{E\})\cap(S(y)\sm\{E\})=\emptyset$. Hence
$$
2(|G|-1)=\sum_{x\in X}(|S(x)|-1)~.
$$
Now for all $g\in G$: $S(gx)=gS(x)g^{-1}$ and thus $|S(gx)|=|S(x)|$; therefore the right hand side equals
$$
\sum_{\wh x\in X/G}(|S(x)|-1)|Gx|~.
$$
Finally by means of exam: $|S(x)|=|G|/|Gx|$ and by division by $|G|$ we obtain:
$$
2-\frac2{|G|}
=\sum_{\wh x\in X/G}\Big(1-\frac{|Gx|}{|G|}\Big)
=\sum_{\wh x\in X/G}\Big(1-\frac{1}{|S(x)|}\Big)~.
$$
As for the solutions to this equation cf. wikipedia. It`s probably a bit more obvious to let $\SO(3)$ and thus $G$ operate on the projective space $P^2(\R)$, because the later is the space of all rotation axes and there is no double-counting.
The orbit $Gx$ of $x\in X$ contains exactly one point if and only if $x\in X_0$. Hence by the previous exam $X$ is the disjoint union of $X_0$ and orbits $Gx_1,\ldots,Gx_n$, whose cardinality is divisible by $p$.
Conjugacy classes of symmetry groups
Since every group of symmetry $G$ is a subgroup of $\OO(3)$, all elements of a conjugacy class have the same type of symmetry. The converse is not true in general: two symmetries in $G$ may have the same type (i.e. they may be conjugate in $\OO(3)$) but they need not be conjugate in $G$! Most computer algebra programs realize finite groups as subgroups of some $S(n)$ (cf. Cayley`s Theorem). To get a list of representatives of all conjugacy classes of e.g. $C_{6v}$ in sage enter
c6v=DihedralGroup(6)
Reps=c6v.conjugacy_classes_representatives()
for g in Reps:
cg=c6v.conjugacy_class(g)
print(g.domain(),len(cg))
This gives you representatives and the cardinalities of the conjugacy classes:
\begin{array}{lll}
((123456), 1),&((165432), 3),&((216543), 3),\\
((234561), 2),&((345612), 2),&((456123), 1)
\end{array}
The characters of finite groups
Suppose we have a finite group, which has exactly $N$ conjugacy classes. Pick a complete set of representatives $g_1=e,g_2,\ldots,g_{N}$ and let $c_1=1,c_2,\ldots,c_{N}$ be the number of elements in the corresponding class, i.e. $c_j$ is the cardinality $|G(g_j)|$ of $C(g_j)$. The table of characters of $G$ will be written as a table with $N+1$ columns and $N+1$ rows: the symbol in the first row and first column is just a symbol for the group. In the remaining columns of the first row we write $1e,c_2g_2,\ldots,c_{N}g_{N}$, indicating the conjugacy class and its cardinality. In the remaining rows of the first column we place symbols for the characters, i.e. $\chi_1,\chi_1,\ldots,\chi_{N}$. Finally for $j,k\in\{1,\ldots,N\}$ we place in row $j+1$ and column $k+1$ the value $\chi_j(g_k)$ of the character $\chi_j$ an the conjugacy class $C(g_k)$:
$$
\begin{array}{c|cccc}
G&1e&c_2g_2&\ldots&c_Ng_N\\
\hline
\chi_1&\chi_1(e)&\chi_1(g_2)&\ldots&\chi_1(g_N)\\
\chi_2&\chi_2(e)&\chi_2(g_2)&\ldots&\chi_2(g_N)\\
\vdots&\vdots&\vdots&\ddots&\vdots\\
\chi_N&\chi_N(e)&\chi_N(g_2)&\ldots&\chi_N(g_N)
\end{array}
$$
For the time being we do not explain how to produce the character table of a given group, we simply fall back to computer algebra systems. It`s here that I`d suggest to familiarize yourself with the relevant commands of the computer algebra system of your choice! The actual construction of characters will be explicated in section. Here we will anticipate a salient feature of this table, which is orthogonality: the columns form an orthogonal basis for $\C^N$ with the canonical complex euclidean product - cf. convolution. Also the rows form an orthonormal set in $\C^N$ with respect to a different complex euclidean product, which will be elucidated in section. However, this is not a deep result, it`s just a consequence of the following
The characters of $C_{2v}$
$C_{2v}$ is isomorphic to $\Z_2^2$ and its character table is given by
$$
\begin{array}{c|rrrr}
C_{2v}&1E&1C_2&1\s_1&1\s_2\\
\hline
\chi_1&1&1&1&1\\
\chi_2&1&1&-1&-1\\
\chi_3&1&-1&1&-1\\
\chi_4&1&-1&-1&1
\end{array}
$$
The characters of $C_{3v}$
Let us return to the site representation of the ammonia molecule $\chem{NH_3}$: The irreducible representations $\Psi_1(g)\colon=\Psi(g)|[e_0]$ and $\Psi_2(g)\colon=\Psi(g)|[x_1]$ feature both the same character: the trivial character $\chi_1(g)=1$. The character $\chi_3$ of the irreducible representation $\Psi_3(g)\colon=\Psi(g)|[x_2,x_3]$ is given by $\chi_3(C_3)=-1$ and $\chi_3(\s_1)=0$. The conjugacy classes of the group $C_{3v}$ are $C(E)=\{E\}$, $C(C_3)=\{C_3,C_3^*\}$ and $C(\s_1)=\{\s_1,\s_2,\s_3\}$. A complete set of representatives is $E,C_3$ and $\s_1$ and the number of elements in the corresponding classes is $1,2$ and $3$. The table of characters looks like this:
$$
\begin{array}{c|rrr}
C_{3v}&1E&2C_3&3\s_1\\
\hline
\chi_1&1&1&1\\
\chi_2&1&1&-1\\
\chi_3&2&-1&0
\end{array}
$$
For our site representation $\Psi$ of ammonia we have: $\tr\Psi=2\chi_1+\chi_3$. This means, that $\Psi$ is the sum of three irreducible sub-representations; two of them are equivalent and feature the character $\chi_1$ and the character of the third is $\chi_3$ - this will be explicated in detail in section.
The characters of $T_d$
Execute in sage the subsequent lines
Td=SymmetricGroup(4)
Reps=Td.conjugacy_classes_representatives()
for g in Reps:
cg=Td.conjugacy_class(g)
print(g.domain(),len(cg))
Td.character_table()
and you will find that $T_d$ has $5$ conjugacy classes of respective size $1,8,3,6,6$ and the table of characters is given by:
$$
\begin{array}{c|rrrrr}
T_d&1E&8C_3&3C_2&6S_4&6\s\\
\hline
\chi_1&1&1&1&1&1\\
\chi_2&1&1&1&-1&-1\\
\chi_3&2&-1&2&0&0\\
\chi_4&3&0&-1&1&-1\\
\chi_5&3&0&-1&-1&1
\end{array}
$$
$\chi_1$ is the character of the trivial representation, $\chi_2$ the character of sign representation, $\chi_5$ the character of the standard representation and $\chi_4$ is the character of the standard representation multiplied by sign, which is a character by exam.
Remark: sage (and most likely any other program) doesn`t give you the types of the representatives but the permutations. Thus you have to find the types by yourself!
The characters of $O_h$
This group has $10$ conjugacy classes, representatives of which are the identity $E$, the inversion $I$, the following matrices with positive determinant:
$$
C_3=\left(\begin{array}{ccc}
0&0&1\\
1&0&0\\
0&1&0
\end{array}\right),
C_2=\left(\begin{array}{ccc}
-1&0&0\\
0&0&1\\
0&1&0
\end{array}\right),
C_4=\left(\begin{array}{ccc}
1&0&0\\
0&0&-1\\
0&1&0
\end{array}\right),
C_4^2=\left(\begin{array}{ccc}
1&0&0\\
0&-1&0\\
0&0&-1
\end{array}\right)
$$
and the following matrices with negative determinant:
$$
S_4=\left(\begin{array}{ccc}
-1&0&0\\
0&0&-1\\
0&1&0
\end{array}\right),
S_6=\left(\begin{array}{ccc}
0&0&-1\\
1&0&0\\
0&1&0
\end{array}\right),
\s_1=\left(\begin{array}{ccc}
1&0&0\\
0&1&0\\
0&0&-1
\end{array}\right),
\s_2=\left(\begin{array}{ccc}
1&0&0\\
0&0&-1\\
0&1&0
\end{array}\right)~.
$$
The table of characters looks as follows:
$$
\begin{array}{c|rrrrrrrrrr}
O_h&1E&8C_3&6C_2&6C_4&3C_4^2&1I&6S_4&8S_6&3\s_1&6\s_2\\
\hline
\chi_1 & 1& 1& 1& 1& 1& 1& 1& 1& 1& 1\\
\chi_2 & 1& 1&-1&-1& 1& 1&-1& 1& 1&-1\\
\chi_3 & 1& 1& 1& 1& 1&-1&-1&-1&-1&-1\\
\chi_4 & 1& 1&-1&-1& 1&-1& 1&-1&-1& 1\\
\chi_5 & 2&-1& 0& 0& 2& 2& 0&-1& 2& 0\\
\chi_6 & 2&-1& 0& 0& 2&-2& 0& 1&-2& 0\\
\chi_7 & 3& 0&-1& 1&-1& 3& 1& 0&-1&-1\\
\chi_8 & 3& 0& 1&-1&-1& 3&-1& 0&-1& 1\\
\chi_9 & 3& 0&-1& 1&-1&-3&-1& 0& 1& 1\\
\chi_{10}& 3& 0& 1&-1&-1&-3& 1& 0& 1&-1
\end{array}
$$
$\chi_1$ is the character of the trivial representation, $\chi_3$ the character of the sign representation, $\chi_9$ the character of the standard representation and $\chi_8$ the character of the standard representation multiplied by sign, which is a character by exam. Execute the following commands in sage
Oh=PermutationGroup([(2,3,4,1),(6,4,5,2),(6,3,5,1),(3,1)])
Reps=Oh.conjugacy_classes_representatives()
for g in Reps:
cg=Oh.conjugacy_class(g)
print(g.domain(),len(cg))
print(Oh.character_table())
and you will get representatives $(123456)$, $(123465)$, $(143265)$, $(153624)$, $(153642)$, $(214365)$, $(234165)$, $(254613)$, $(254631)$, $(341265)$ and sizes $1,3,3,6,6,6,6,8,8,1$ of conjugacy classes as well as the table of characters of $O_h$ - of course, the order of conjugacy classes and the order of characters may differ from the orders in the table above!
The characters of $A(5)$
The following list of sage commands:
Al=AlternatingGroup(5)
Reps=Al.conjugacy_classes_representatives()
for g in Reps:
cg=Al.conjugacy_class(g)
print(g.domain(),len(cg))
print(Al.character_table())
gives representatives of the conjugacy classes: $E\colon=(12345)$, $A\colon=(21435)$, $B\colon=(23145)$, $C\colon=(23451)$, $D\colon=(23514)$, their sizes: $1,15,20,12,12$ and the table of characters:
$$
\begin{array}{c|rrrcc}
A(5)&1E&15A&20B&12C&12D\\
\hline
\chi_1&1 & 1 & 1 & 1 & 1 \\
\chi_2&3 & -1 & 0 & \zeta_{5}^{3} + \zeta_{5}^{2} + 1 & -\zeta_{5}^{3} - \zeta_{5}^{2} \\
\chi_3&3 & -1 & 0 & -\zeta_{5}^{3} - \zeta_{5}^{2} & \zeta_{5}^{3} + \zeta_{5}^{2} + 1 \\
\chi_4&4 & 0 & 1 & -1 & -1 \\
\chi_5&5 & 1 & -1 & 0 & 0
\end{array}
$$
where $\zeta_5\colon=e^{2\pi i/5}$. For additional character tables important in chemistry cf. wikipedia. Of course, all these groups can be handled by sage, gap, etc.
The characters of $C_{nv}$, $n\geq4$
We have $C_{nv}=\{\s^jC_n^k:j=0,1,k=0,\ldots,n-1\}$ with rotations $C_n^0=E,\ldots,C_n^{n-1}$ and reflections $\s C_n^0,\ldots,\s C_n^{n-1}$; since: $C_n^k\s=\s C_n^{n-k}$, we get the following conjugacy classes:
$$
C(E)=\{E\},
C(C_n^k)=\{C_n^k,C_n^{n-k}\},
C(\s C_n^k)=\{\s C_n^{k-2l}:l\in\N_0\}~.
$$
If $n$ is even, then we get $1+[n/2]+2=(n+6)/2$ conjugacy classes with $1+(2[n/2]-1)+2[n/2]=2n$ elements and if $n$ is odd we have $1+[n/2]+1=(n+3)/2$ conjugacy classes with $1+2[n/2]+n=2n$ elements. In any case we have found all conjugacy classes and a complete list of representatives thereof.
For $n=5$ the conjugacy classes are: $\{E\},\{C,C^4\},\{C^2,C^3\},\{\s,\s C^3,\s C^1,\s C^4,\s C^2\}$ and for $n=6$: $\{E\},\{C,C^5\},\{C^2,C^4\},\{C^3\},\{\s,\s C^4,\s C^2\},\{\s C^1,\s C^5,\s C^3\}$
A one-dimensional unitary representation is just a homomorphism $\chi:C_{nv}\rar S^1$, thus: $\chi(\s)=\pm1$; since $\s C_n=C_n^{-1}\s$, we must have $\chi(C_n)^2=1$, i.e. $\chi(C_n)=\pm1$. Hence there are at most $4$ one-dimensional representations; in fact if $n$ is even there are exactly $4$ - we provide the values of these homomorphisms on the conjugacy classes of the two generators $C_n$ and $\s$ only:
$$
\begin{array}{r|rr}
C_{nv}&2C_n&(n/2)\s\\
\hline
\chi_1&1&1\\
\chi_2&1&-1\\
\chi_3&-1&1\\
\chi_4&-1&-1
\end{array}
$$
If $n$ is odd then only the first two extend to homomorphisms on $C_{nv}$, because $C_n^n=E$ and thus $1=\chi_3(C_n^n)=(-1)^n$. There is also a bunch of irreducible representations of dimension two: for $j\in\{0,\ldots,n-1\}$ we put
$$
\Psi_j(C_n)
=\left(\begin{array}{cc}
e^{2\pi ij/n}&0\\
0&e^{-2\pi ij/n}
\end{array}\right),\quad
\Psi_j(\s)
=\left(\begin{array}{cc}
0&1\\
1&0
\end{array}\right)~.
$$
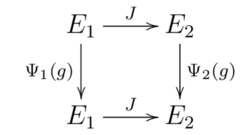
It can be verified easily that $\Psi_j(C_n)^n=1=\Psi_j(\s)^2$ and $\Psi_j(\s)\Psi_j(C_n)=\Psi_j(C_n)^{-1}\Psi_j(\s)$ and therefore all mappings $\Psi_j$ extend to homomorphisms $\Psi_j:C_{nv}\rar\UU(2)$ and we have $\Psi_{n+j}=\Psi_j$. Putting $J\colon=\Psi_j(\s)$, we get:
\begin{eqnarray*}
J\Psi_j(C_n)
&=&\Psi_j(\s C_n)=\Psi_j(C_n^{-1}\s)=\Psi_{n-j}(C_n)J\\
J\Psi_j(\s)&=&\Psi_{-j}(\s)\Psi_j(\s)=\Psi_{n-j}(\s)J,
\end{eqnarray*}
thus $J\Psi_j=\Psi_{n-j}J$, consequently $\Psi_j$ and $\Psi_{n-j}$ are equivalent. Since we are only interested in in-equivalent representations, we may assume: $0\leq j\leq[n/2]$. For $j=0$ we have $\tr\Psi_0=\chi_1+\chi_2$, which implies as we will see that $\Psi_0$ is the sum of two irreducible representations with characters $\chi_1$ and $\chi_2$, and indeed the corresponding sub-spaces are $\lhull{e_1-e_2}$ and $\lhull{e_1+e_2}$. Also for $n$ even we have: $\tr\Psi_{n/2}=\chi_3+\chi_4$, indicating that $\Psi_{n/2}$ is the sum of two irreducible representations with characters $\chi_3$ and $\chi_4$.
Moreover, they are pairwise in-equivalent: if $\Psi_j$ and $\Psi_k$ are equivalent, i.e. if there is some $A\in\Gl(2,\C)$ such that $A\Psi_j=\Psi_kA$, then it follows that $\Psi_j(C_n)$ and $\Psi_k(C_n)$ have the same eigenvalues, i.e. $e^{2\pi ij/n}=e^{\pm2\pi ik/n}$, thus either $j+k=0\,\modul(n)$ or $j-k=0\,\modul(n)$. For even $n$ we`ve found $(n+6)/2$ pairwise in-equivalent irreducible representations and for odd $n$ we`ve got $(n+3)/2$ such entities, which coincides with the number of conjugacy classes and therefor these are all pairwise in-equivalent irreducible representations of $C_{nv}$. Consequently for $n$ even and $j\in\{1,\ldots,n/2-1\}$ we get the following table of characters:
$$
\begin{array}{r|cr}
C_{nv}&2C_n&(n/2)\s\\
\hline
\chi_1&1&1\\
\chi_2&1&-1\\
\chi_3&-1&1\\
\chi_4&-1&-1\\
\psi_j&2\cos(2\pi j/n)&0
\end{array}
$$
Since $\chi_j$ are homomorphisms the value of $\chi_j$ at any element is determined by its values at the generators $C_n$ and $\s$. However, the values of the characters $\psi_j$ at any element of $C_{nv}$ must be calculated via the representations:
$$
\psi_j(\s C_n^k)=\tr(\Psi_j(\s)\Psi_j(C_n)^k)=0,
\psi_j(C_n^k)=\tr\Psi_j(C_n)^k=2\cos(2\pi jk/n)~.
$$
The characters of commutative groups
We will see below (cf. corollary) that every irreducible representation of a commutative group $G$ is one-dimensional and that there are exactly $|G|$ in-equivalent irreducible representations, for each conjugacy class contains exactly one element. Thus the characters determine all representations and every character is a homomorphism $\chi:G\rar S^1$.
For all $y\in\Z_n^d$ the mapping $\chi_y$ is obviously a homomorphism and $\chi_y=\chi_z$ iff for all $x\in\Z_n^d$: $\la x,y-z\ra=0$ in $\Z_n$ but this only holds iff $y$ and $z$ coincide. Hence we`ve got $|\Z_n^d|$ pairwise distinct homomorphisms $\chi_y:\Z_n^d\rar S^1$, i.e. all characters of $\Z_n^d$. Therefore we can identify the dual of $\Z_n^d$ with $\Z_n^d$, i.e. $\Z_n^d$ is self-dual. Since any finite commutative group $G$ is isomorphic to a direct product of cyclic groups (cf. wikipedia) and the characters of a product group is the tensor product of the characters, all characters of $G$ can be computed!
The characters of $S(n)$
By Cayley's Theorem every group of order $n$ is isomorphic to some subgroup of $S(n)$. Thus it's of interest to know all characters of $S(n)$, which are not at all easy to find. We will just determine the number of characters, i.e. the number of conjugacy classes: Every permutation $\pi\in S(n)$ is composition of pairwise disjoint cycles (cf. wikipedia) - since the cycles are disjoint, they commute. So let us first compute the conjugacy class of a cycle $\t=(n_1,\ldots,n_k)$ of length $k\geq2$, i.e. the permutation $n_1\mapsto n_2\mapsto\cdots\mapsto n_{k-1}\mapsto n_k\mapsto n_1$ - cycles of length $2$ are called transpositions. Since $\pi\t\pi^{-1}(\pi(n_j))=\pi(\t(n_j))=\pi(n_{j+1})$, it follows that $\pi\t\pi^{-1}$ is the cycle $(\pi(n_1),\ldots,\pi(n_k))$.
By a partition of $n$ we understand a representation $n=l_1+l_2+\cdots+l_m$ as sum of natural numbers $l_1,\ldots,l_m$ such that $l_1\geq l_2\geq\cdots\geq l_m$ for some $m\in\{1,\ldots,n\}$. If $\pi=\t_1\cdots\t_k$ is a decomposition of $\pi$ into disjoint cycles of lengths $l_1\geq\cdots\geq l_m$, then the sum $L\colon=l_1+\cdots+l_m$ is usually smaller than $n$ - the difference $n-L$ is just the number of fixed points; put $l_{m+1}=\ldots=l_{m+n-L}=1$. This way we get for every permutation a partition $l_1,\ldots,l_k$ of $n$. For example the partition associated with a transposition is $2,1,\ldots,1$ and the partition associated with a single cycle of length $l$: $l,1,\ldots,1$.
If $\pi,\s$ induce the same partition $(l_1,\ldots,l_k)$, then
$$
\pi=\t_1\cdots\t_k,\quad
\s=\r_1\cdots\r_k
$$
where $\t_j=(n_{j1},\ldots,n_{jl_j})$ and $\r_j=(m_{j1},\ldots,m_{jl_j})$. Put $\a(n_{ji})\colon=m_{ji}$, then it follows that: $\a\t_j\a^{-1}=\r_j$ and therefore:
$$
\a\pi\a^{-1}=(\a\t_1\a^{-1})\cdots(\a\t_k\a^{-1})=\r_1\cdots\r_k=\s~.
$$
If $\pi=\t_1\cdots\t_k$ and $\s=\a\pi\a^{-1}$, then $\s=\a\t_1\a^{-1}\cdots\a\t_k\a^{-1}$ and hence $\pi$ and $\s$ induce the same partition.
$\eofproof$
Thus we can identify the set of conjugacy classes of $S(n)$ with the set of partitions of $n$.
As for the characters of $S(n)$ cf. e.g. Murnaghan-Nakayama Rule or Frobenius Method.
Some examples in sage
To get the character table of e.g. $C_{6v}$ in sage enter
c6v=DihedralGroup(6)
Reps=c6v.conjugacy_classes_representatives()
for g in Reps:
cg=c6v.conjugacy_class(g)
print(g.domain(),len(cg))
latex(c6v.character_table())
This gives you the following representatives: $E=(123456)$, $A=(165432)$, $B=(216543)$, $C=(234561)$, $D=(345612)$, $F=(456123)$ of size $1,3,3,2,2,1$ and the character table:
\begin{array}{c|rrrrrr}
C_{6v}&1E&3A&3B&2C&2D&1F\\
\hline
\chi_1&1 & 1 & 1 & 1 & 1 & 1 \\
\chi_2&1 & -1 & -1 & 1 & 1 & 1 \\
\chi_3&1 & -1 & 1 & -1 & 1 & -1 \\
\chi_4&1 & 1 & -1 & -1 & 1 & -1 \\
\chi_5&2 & 0 & 0 & 1 & -1 & -2 \\
\chi_6&2 & 0 & 0 & -1 & -1 & 2
\end{array}
For $C_{5v}$ we get the representatives: $E=(12345)$, $A=(15432)$, $B=(23451)$, $C=(34512)$ of size $1,5,2,1$ and the character table:
\begin{array}{c|rrcc}
C_{5v}&1E&5A&2B&1C\\
\hline
\chi_1&1 & 1 & 1 & 1 \\
\chi_2&1 & -1 & 1 & 1 \\
\chi_3&2 & 0 & \zeta_{5}^{3} + \zeta_{5}^{2} & -\zeta_{5}^{3} - \zeta_{5}^{2} - 1 \\
\chi_4&2 & 0 & -\zeta_{5}^{3} - \zeta_{5}^{2} - 1 & \zeta_{5}^{3} + \zeta_{5}^{2}
\end{array}
where $\zeta_5\colon=e^{2\pi i/5}$. Alternatively you may use in sage the gap interface; for the subgroup $G$ of $S(4)$ generated by $(1,2)(3,4)$ and $(1,2,3)$:
gap.eval("G:=Group((1,2)(3,4),(1,2,3))")
gap.eval("T:=CharacterTable(G)")
gap.eval("SizesConjugacyClasses(T)")
print(gap.eval("irr:=Irr(G)"))
The linear group $\Gl(2,\Z_3)$ of the vector-space $\Z_3^2$, which has order $48$ and
G=GL(2,3)
Reps=G.conjugacy_classes_representatives()
for g in Reps:
cg=G.conjugacy_class(g)
print(g.domain(),len(cg))
print(G.character_table())
gives you $8$ conjugacy classes, representatives thereof are:
$$
E=\left(\begin{array}{cc}
1&0\\
0&1
\end{array}\right),
A=\left(\begin{array}{cc}
0&2\\
1&1
\end{array}\right),
B=\left(\begin{array}{cc}
2&0\\
0&2
\end{array}\right),
C=\left(\begin{array}{cc}
0&2\\
1&2
\end{array}\right)
$$
and
$$
D=\left(\begin{array}{cc}
0&2\\
1&0
\end{array}\right),
F=\left(\begin{array}{cc}
0&1\\
1&2
\end{array}\right),
G=\left(\begin{array}{cc}
0&1\\
1&1
\end{array}\right),
H=\left(\begin{array}{cc}
2&0\\
0&1
\end{array}\right),
$$
sizes: $1,8,1,8,6,6,6,12$ and the character table:
$$
\begin{array}{c|rrrrrccr}
\Gl(2,\Z_3)&1E&8A&1B&8C&6D&6F&6G&12H\\
\hline
\chi_1&1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
\chi_2&1 & 1 & 1 & 1 & 1 & -1 & -1 & -1 \\
\chi_3&2 & -1 & 2 & -1 & 2 & 0 & 0 & 0 \\
\chi_4&2 & 1 & -2 & -1 & 0 & -\zeta_{8}^{3} - \zeta_{8} & \zeta_{8}^{3} + \zeta_{8} & 0 \\
\chi_5&2 & 1 & -2 & -1 & 0 & \zeta_{8}^{3} + \zeta_{8} & -\zeta_{8}^{3} - \zeta_{8} & 0 \\
\chi_6&3 & 0 & 3 & 0 & -1 & 1 & 1 & -1 \\
\chi_7&3 & 0 & 3 & 0 & -1 & -1 & -1 & 1 \\
\chi_8&4 & -1 & -4 & 1 & 0 & 0 & 0 & 0
\end{array}
$$
where $\zeta_8\colon=e^{2\pi i/8}$. Here is another alternative: 'chi.adams_operation(k).values()' gives you the value of the character $\chi$ at the group element $g^k$, where $g$ runs through a complete set of representatives of the conjugacy classes:
G=GL(2,3)
Chars=G.irreducible_characters()
Reps=G.conjugacy_classes_representatives()
for chi in Chars:
chi.adams_operation(1).values()
Here are some other examples of matrix groups: A subgroup of $\Gl(2,\Z_5)$ generated by two matrices:
F=GF(5)
Gen=[matrix(F,2,[1,2,4,1]), matrix(F,2,[1,1,0,1])]
G=MatrixGroup(Gen)
Chars=G.irreducible_characters()
for chi in Chars:
chi.adams_operation(1).values()
The groups $\Sp(4,\Z_3)$, $\SO(3,\Z_2)$, $\Sl(2,\Z_5)$ and a subgroup of $S(6)$ with two generators and certain elements:
G=Sp(4,GF(3))
H=SO(3,GF(2))
HP=H.as_permutation_group()
for g in H:
print(g.domain())
HF=HP.as_finitely_presented_group()
J=SL(2,GF(5))
K=PermutationGroup(['(1,2)(3,4)','(3,4,5,6)'])
g=K('(1,2)(3,5,6)')
h=K([2,1,5,4,6,3])
g==h
gh=g*h; gh
Beware, in sage $g*h$ is the permutation $h\circ g$!
Subgroups
Suppose $\chi$ is a character of a subgroup $H$ of $G$. In general $\chi$ is not the restriction of a character of $G$. However we can construct a compound character of $G$: we first expand $\chi:G\rar\C$ by putting $\chi|H^c=0$ and then define $\chi^G:G\rar\C$ by
$$
\chi^G(g)
\colon=\frac1{|H|}\sum_{x\in G}\chi(xgx^{-1})~.
$$
Of course, $\chi^G$ is a class function (cf. e.g. exam) and we will actually see that it`s a compound character of $G$. But first of all we`d like to indicate that $\chi$ is in general not the restriction of $\chi^G$ to $H$: take e.g. the trivial character $\chi=1$, then
$$
\chi^G(g)=\frac{|\{x\in G:xgx^{-1}\in H\}|}{|H|}~.
$$
The mapping $u:G\rar C(g)$, $x\mapsto xgx^{-1}$, is by definition of $C(g)$ onto and $u(x)=u(y)$ iff $y^{-1}xgx^{-1}y=g$, i.e. iff $x^{-1}y\in Z(g)$. It follows that for any subset $A$ of $G$:
$$
|\{x\in G:xgx^{-1}\in A\}|
=|A\cap C(g)||Z(g)|
=|A\cap C(g)||G|/|C(g)|
$$
Therefore we conclude
\begin{equation}\label{subeq1}\tag{SUB1}
\chi^G(g)=\frac{|G||H\cap C(g)|}{|H||C(g)|}
\end{equation}
which need not be constant on $H$. However, the following result shows amongst others that it`s for all $g\in G$ a non-negative integer.
$\proof$
For all $x\in H$: $\chi(xgx^{-1})=\chi(g)$. Indeed, for $g\in H$ the elements $xgx^{-1}$ and $g$ are conjugate in $H$ and since $\chi$ is a class function on $H$: $\chi(xgx^{-1})=\chi(g)$. If $g\notin H$, then $xgx^{-1}\notin H$ and thus both sides vanish.
1. Now suppose $y\in Hx$, then $\chi(ygy^{-1})=\chi(hxgx^{-1}h^{-1})=\chi(xgx^{-1})$ and therefore the function $y\mapsto\chi(ygy^{-1})$ is constant on cosets $Hx$, i.e.:
$$
\frac1{|H|}\sum_{x\in G}\chi(xgx^{-1})
=\sum_{j=1}^m\chi(x_jgx_j^{-1})~.
$$
2. By definition of the euclidean product we get for every character $\psi$ of $G$:
\begin{eqnarray*}
\la\chi^G,\psi\ra_{L_2(G)}
&=&\frac1{|G|}\sum_{g\in G}\chi^G(g)\cl{\psi(g)}\\
&=&\frac1{|G||H|}\sum_{x\in G}\sum_{g\in G}\chi(xgx^{-1})\cl{\psi(g)}
=\frac1{|G||H|}\sum_{x\in G}\sum_{g\in G}\chi(g)\cl{\psi(x^{-1}gx)}\\
&=&\frac1{|G||H|}\sum_{g,x\in G}\chi(g)\cl{\psi(g)}
=\frac1{|H|}\sum_{g\in G}\chi(g)\cl{\psi(g)}\\
&=&\frac1{|H|}\sum_{g\in H}\chi(g)\cl{\psi(g)}
=\la\chi,\psi\ra_{L_2(H)}~.
\end{eqnarray*}
3. It remains to show that $\chi^G$ is a compound character of $G$. Since $\chi^G$ is a class function, $\chi^G$ is a linear combination of characters by theorem and we are left to prove that for all characters $\psi$ of $G$: $\la\chi^G,\psi\ra_{L_2(G)}\in\N_0$. Now, by 2. we have:
$$
\la\chi^G,\psi\ra_{L_2(G)}
=\la\chi,\psi\ra_{L_2(H)}
$$
which is a non-negative integer by \eqref{goteq3}, because the restriction of $\psi$ to $H$ is a compound character of $H$.
$\eofproof$
The above construction isn`t specific to characters, it can be done for an arbitrary class function $\chi$ of $H$ and thus it gives rise to a linear map
$$
I:Z(H)\rar Z(G),\quad\chi\mapsto\chi^G~.
$$
This map also satisfies the relation $\la I(\chi),\psi\ra_{L_2(G)}=\la\chi,\psi\ra_{L_2(H)}$, which merely says that its adjoint $I^*$ is the restriction $R:Z(G)\rar Z(H)$, $\psi\mapsto\psi|H$. Or conversely, the map $I$ is the adjoint of $R$. Thus we could have started as well with the problem of finding the adjoint of the more natural restriction map $R:Z(G)\rar Z(H)$. $I$ is not necessarily injective, because the restriction map $R:Z(G)\rar Z(H)$ may not be onto.
Theorem is particularly useful if $G$ has a big commutative subgroup $H$, because these subgroups have lots of characters and all of them are homomorphisms $G\rar S^1$. Take e.g. the dihedral group $G=C_{nv}$ and the cyclic subgroup $H=\Z_n$. There are two right co-sets with representatives $E$ and $\s$, i.e. $\chi^G(g)=\chi(g)+\chi(\s g\s)$:
$$
\chi^G(\s)=2\chi(\s)=0
\quad\mbox{and}\quad
\chi^G(C_n)=\chi(C_n)+\chi(C_n^{-1})~.
$$
For $\chi(C_n^j)=e^{2\pi ikj/n}$ we get: $\chi^G(\s)=0$ and $\chi^G(C_n)=2\cos(2\pi k/n)$. This is actually a character of $C_{nv}$ of a two dimensional irreducible representation, because
As $S(2)$ is commutative of order $2$ we get the following table of characters:
$$
\begin{array}{c|rr}
S(2)&1(12)&1(21)\\
\hline
\chi_1&1&1\\
\chi_2&1&-1
\end{array}
$$
$S(3)$ has three classes $C_1=\{(123)\}$, $C_2=\{(231),(312)\}$, $C_3=\{(213),(132),(321)\}$ and $|C_1|=1$, $|C_2|=2$, $|C_3|=3$. We already know two characters: the trivial character $\psi_1=1$ and $\psi_2=\sign$, so we have:
$$
\begin{array}{c|rrr}
S(3)&1(123)&2(231)&3(213)\\
\hline
\psi_1&1&1&1\\
\psi_2&1&1&-1\\
\psi_3&x&y&z
\end{array}
$$
We identify $S(2)$ with the subgroup $H=\{(123),(213)\}$ of $S(3)$ and employ \eqref{subeq1} to get an induced character of $S(3)$: $|H\cap C_1|=1$, $|H\cap C_2|=0$ and $|H\cap C_3|=1$. For $\chi_1$ we get that $\chi_1^G((123))=3$, $\chi_1^G((231))=0$ and $\chi_1^G((213))=1$ is an induced character, i.e. for some $m_1,m_2,m_3\in\N_0$: $m_1\psi_1+m_2\psi_2+m_3\psi_3=\chi_1^G$, where $m_1=\la\chi_1^G,\psi_1\ra=(3+0+3)/6=1$ and $m_2=\la\chi_1^G,\psi_2\ra=(3+0-3)/6=0$. Thus we are left with $m_3\psi_3=\chi_1^G-\psi_1$, which gives us three equations:
$$
m_3x=2,\quad
m_3y=-1,\quad
m_3z=0
$$
and only one solution: $z=0$, $m_3=1$, $y=-1$ and $x=2$.
We consider $O_h$ as a subgroup of $S(6)$ and the subgroup of reflections about the coordinate planes is $H$. In sage this can be done as follows: To get the elements of $H$ enter
H=PermutationGroup([(5,6),(1,3),(2,4)])
for g in H:
print(g.domain())
with eight elements of $H$:
$$
(123456),(123465),(143256),(143265),(321456),(321465),(341256),(341265)~.
$$
A complete list of representatives for the right co-sets can be obtained from:
Oh=PermutationGroup([(2,3,4,1),(6,4,5,2),(6,3,5,1),(3,1)])
Cosets=Oh.cosets(H, side='right')
for c in Cosets:
print(c[0].domain())
which produces the output:
$$
(123456),
(153624),
(214356),
(254613),
(516324),
(526413)~.
$$
Now let's take the trivial character $\chi=1$ of $H$, then by \eqref{subeq1}
$$
\chi^G(g)=\frac{|G||H\cap C(g)|}{|H||C(g)|}=\frac{6|H\cap C(g)|}{|C(g)|}
$$
and we are essentially left with the computation of the cardinality of $H\cap C(g)$:
Reps=Oh.conjugacy_classes_representatives()
coh=len(Oh)
ch=len(H)
for g in Reps:
cg=Oh.conjugacy_class(g)
hsg=set(cg) & set(H)
print(g,(coh*len(hsg))/(ch*len(cg)))
This gives the induced character $\chi^G$: it's $6$ times the indicator function of the union of the following conjugacy classes
$$
C(())\cup C((5,6))\cup C((2,4)(5,6))\cup C((1,3)(2,4)(5,6))
=C(E)\cup C(\s_1)\cup C(C_4^2)\cup C(I)~.
$$
Since $\Vert\chi^G\Vert_{L_2(O_h)}=\sqrt6$ it`s either the sum of $6$ characters or the sum of $3$ characters one with multiplicity $2$.
Of course sage has some built-in functions to produce induced characters:
Oh=PermutationGroup([(2,3,4,1),(6,4,5,2),(6,3,5,1),(3,1)])
H=Oh.subgroup([(5,6),(1,3),(2,4)])
for chi in H.irreducible_characters():
print(chi.induct(Oh).values())
The output exhibits the values of the induced characters on the 10 conjugacy classes. It will give us essentially four induced characters; the norm of the first two is $\sqrt6$ and the remaining two have norm $\sqrt2$. If you start with an arbitrary class function of $H$ just execute
chi=ClassFunction(H, [-1,-1,-1,-1,0,0,0,0])
print(chi.induct(Oh).values())
Quotients
If $H$ is a normal subgroup of $G$, then a representation $\Psi:G\rar\UU(E)$ of $G$ descends to a representation of $G/H$ iff for all $h\in H$: $\Psi(h)=1_E$. On the other hand any representation $\wh\Psi$ of $G/H$ extends to a representation $\Psi$ of $G$: simply define $\Psi(g)\colon=\wh\Psi(\pi(g))$, where $\pi$ is the quotient map. This way the irreducible representations of the quotient $G/H$ can be identified with the subset $H^\perp$ of $\wh G$ defined by
$$
H^\perp\colon=\{\Psi\in\wh G:\forall h\in H:\quad\Psi(h)=1\}~.
$$
The characters of $G$ can be determined provided $G$ has plenty of normal subgroups and the characters of the quotients are known. A prominent example thereof is the quaternion group, cf. subsection.
Frobenius Reciprocity Theorem
Given a representation $\Psi$ of $H$ with character $\chi$, can we produce a representation $\Psi^G$ of $G$ with $\tr\Psi^G=\chi^G$? Remember the induced representation of $\Psi:H\rar\Gl(E)$, defined in subsection: it`s a representation of $G$ in the vector-space
$$
E^G=\{f:G\rar E:\forall h\in H\,\forall x\in G: f(hx)=\Psi(h)(f(x))\}
$$
given by
$$
\forall g,x\in G:\quad
\Psi^G(g)f(x)=f(xg)~.
$$
$\proof$
Remember, if $\vp\in\Hom_G(\Phi,\Psi^G)$ and $\psi\in\Hom_H(\Phi,\Psi)$, then we have:
$$
\vp(\Phi(g)y)=\Psi^G(g)(\vp(y))
\quad\mbox{and}\quad
\psi(\Phi(h)x)=\Psi(h)(\psi(x))
$$
1. Suppose $\vp\in\Hom_G(\Phi,\Psi^G)$, we must prove that $\psi\in\Hom_H(\Phi,\Psi)$:
\begin{eqnarray*}
\psi(\Phi(h)y)
&=&\vp(\Phi(h)y)(e)
=\Psi^G(h)(\vp(y))(e)
=\vp(y)(eh)\\
&=&\vp(y)(he)
=\Psi(h)(\vp(y)(e))
=\Psi(h)(\psi(y)),
\end{eqnarray*}
i.e. $\psi\in\Hom_H(\Phi,\Psi)$.
2. Conversely, suppose $\psi\in\Hom_H(\Phi,\Psi)$, then we have to prove that $\vp\in\Hom_G(\Phi,\Psi^G)$:
\begin{eqnarray*}
\vp(\Phi(g)y)(x)
&=&\psi(\Phi(x)\Phi(g)y)
=\Psi(xg)(\psi(y))\\
&=&\psi(\Phi(xg)y)
=\vp(y)(xg)
=\Psi^G(g)(\vp(y))(x),
\end{eqnarray*}
i.e. $\vp\in\Hom_G(\Phi,\Psi^G)$.
3. These maps are inverse of each other: suppose $\vp$ is given; putting $\psi(y)=\vp(y)(e)$, we get by the definition of $\Psi^G$:
$$
\psi(\Phi(g)y)
=\vp(\Phi(g)y)(e)
=\Psi^G(g)(\vp(y))(e)
=\vp(y)(g)
$$
and analogously: given $\psi$ and putting $\vp(y)(g)\colon=\psi(\Phi(g)y)$ it follows that $\vp(y)(e)=\psi(\Phi(g)y)=\psi(y)$.
$\eofproof$
$\proof$
Put $\wt\chi(g)\colon=\tr\Psi^G(g)$ and suppose $\Phi:G\rar\UU(F)$ is irreducible with character $\r$, then by corollary, theorem and theorem we conclude:
$$
\la\wt\chi,\r\ra_{L_2(G)}
=\dim\Hom_G(\Phi,\Psi^G)
=\dim\Hom_H(\Phi,\Psi)
=\la\chi,\r\ra_{L_2(H)}
=\la\chi^G,\r\ra_{L_2(G)}~.
$$
Since the characters of $G$ form a basis of $Z(G)$ and both $\wt\chi$ and $\chi^G$ are in $Z(G)$, it follows that $\wt\chi=\chi^G$.
$\eofproof$
We just have to compute $\Psi^G(g)f_j(x)=f_j(xg)$. For any $g\in G$ the co-sets $Hx_1g,\ldots,Hx_mg$ are just a permutation $Hx_{\pi(1)},\ldots,Hx_{\pi(m)}$ of the co-sets $Hx_1,\ldots,Hx_m$ and thus $\Psi^G(g)$ maps the basis $f_j$ onto the basis $f_{\pi(j)}$.
Abelianization and Abelian subgroups
How many one-dimensional in-equivalent representations of a finite group $G$ do exist? If $f:G\rar S^1$ is a homomorphism, then for all $x,y\in G$: $f(x^{-1}y^{-1}xy)=1$. Thus the commutator subgroup $[G,G]$ generated by all its commutators $[x,y]\colon=x^{-1}y^{-1}xy$ must be in the kernel of $f$.
$[G,G]$ is normal and the quotient $G/[G,G]$ is commutative - it`s called the abelianization of $G$, for $xy=yx[x,y]$ and thus $yx$ and $xy$ are in the same class. Moreover, by the above considerations every homomorphism $f:G\rar H$ in a commutative group $H$ descends to a unique homomorphism $\wh f:G/[G,G]\rar H$ such that $f=\wh f\circ\pi$, where $\pi:G\rar[G,G]$ is the quotient map. Thus there are exactly $|G/[G,G]|$ mutually in-equivalent one-dimensional representations.
In sage this can be done as follows:
Q=QuaternionGroup()
CQ=Q.cayley_table()
head=CQ.row_keys()
n=Q.order()
for i in range(n):
print(head[i].domain())
Q.cayley_table()
Q.commutator()
F=Q.as_finitely_presented_group()
F.abelian_invariants()
This will realize $Q$ as a subgroup of $S(8)$, it will exhibit the Cayley table of $Q$ with elements $a,b,c,d,e,f,g,h$ (neutral element: $a$) and what permutations these elements stand for. It will tell you that the commutator subgroup $[Q,Q]$ is $\{a,c\}$ and that $Q/[Q,Q]$ is isomorphic to $\Z_2\times\Z_2$. Thus $Q$ has exactly four one-dimensional irreducible representations. Since the characters of $\Z_2^2$ are known, we can construct all four homomorphisms $\chi_j:Q\rar S^1$. The left co-sets are: $\{a,c\}$, $\{b,d\}$, $\{e,g\}$, $\{f,h\}$, and the homomorphisms $\chi_j:Q\rar S^1$ are therefore given by
$$
\begin{array}{c|rrrr}
&\{a,c\}&\{b,d\}&\{e,g\}&\{f,h\}\\
\hline
\chi_1&1&1&1&1\\
\chi_2&1&1&-1&-1\\
\chi_3&1&-1&1&-1\\
\chi_4&1&-1&-1&1
\end{array}
$$
To get representatives and sizes of the conjugacy classes enter:
Reps=Q.conjugacy_classes_representatives()
for g in Reps:
cg=Q.conjugacy_class(g)
print(g.domain(),len(cg))
Now we can set up the table of homomorphisms $\chi_j:Q\rar S^1$:
$$
\begin{array}{c|rrrrr}
Q&1a&2d&1c&2e&2f\\
\hline
\chi_1&1&1&1&1&1\\
\chi_2&1&1&1&-1&-1\\
\chi_3&1&-1&1&1&-1\\
\chi_4&1&-1&1&-1&1
\end{array}
$$
The dimension of the fifth character must be $2$ (since $4+2^2=8$) and by orthogonality of the columns we conclude: $\chi_5(d)=0$, $\chi_5(c)=-2$, $\chi_5(e)=0$ and $\chi_5(f)=0$.
For the following examples you are strongly advised to use a computer algebra system!
The Laplacian $\D_R:L_2(G)\rar L_2(G)$ of $(G,R)$ is defined by
$$
\D_Rf(y)
\colon=-\sum_{z\in Ry}(f(z)-f(y))
=-\sum_{x\in R}\nabla_xf(y)
$$
where for all $x\in R$ and all $y\in G$: $\nabla_xf(y)\colon=f(xy)-f(y)$.
It is easily checked that $\D_R=|R|-|G|A_R$ or
$$
\D_Rf(x)=|R|f(x)-\sum_{y\in G}a(x,y)f(y)
$$
where $(a(x,y))$ is the adjacency matrix. It follows that $\D_R$ is self-adjoint and all its eigen-values lie in the interval $[0,2|R|]$, i.e. $\D_R$ is a positive definite operator. The linear differential equation $u^\prime(t)=-\D_Ru(t)$ for $u:\R_0^+\rar L_2(G)$ is called the heat equation for the Cayley graph $(G,R)$; given $u(0)=f\in L_2(G)$, the unique solution is $u(t)=e^{-t\D_R}f$.