← Index → Homogene Räume
Diese Vorlesung beruht auf einer Vorlesung von K. Kiener über Fourierreihen. Voraussetzungen: Maß- und Integrationstheorie (e.g. P.R. Halmos) und elementare Funktionalanalysis.

Fourierreihen und trigonometrische Reihen

Allgemeines

Die Quotientengruppe $\TT\colon=\R/2\pi\Z$ heißt der (eindimensionale) Torus (die Addition ist die gewöhnliche Addition zweier reeller Zahlen modulo $2\pi$). Zu jeder $2\pi$-periodischen Funktionen $f:\R\rar\C$ gibt es genau eine Funktion $f_\TT:\TT\rar\C$, so daß für alle $x\in\R$: $f_\TT([x])=f(x)$ ($[.]:\R\rar\TT$ ist hierbei die Quotientenabbildung) und umgekehrt gibt es zu jeder Abbildung $F:\TT\rar\C$ genau eine $2\pi$-periodische Abbildung $f:\R\rar\C$ mit $F=f_\TT$. Bezeichnet ferner $S^1$ die multiplikativen Gruppe $S^1\colon=\{z\in\C:|z|=1\}$ und $e:\R\rar S^1$ den Homomorphismus $x\mapsto e^{ix}$, so ist $e_\TT:\TT\rar S^1$ ein Isomorphismus. Eine $2\pi$-periodische Abbildung $f:\R\rar\C$ können wir daher entweder als Abbildung von $\TT$ in $\C$ oder als Abbildung von $S^1$ in $\C$ betrachten.
Im folgenden bezeichnen wir mit $\l$ das Lebesguemaß und für $1\leq p\leq\infty$ mit $L_p(\TT)$ die Menge aller Lebesgue-meßbaren $2\pi$-periodischen Funktionen $f:\R\rar\C$, für die gilt: $\int_{-\pi}^{\pi}|f|^p\,d\l<\infty$. Weiters setzen wir für $1\leq p<\infty$: \begin{equation}\label{allgeq1}\tag{ALG1} \norm f_p\colon=\Big(\frac1{2\pi}\int_{-\pi}^{\pi}|f(t)|^p\,dt\Big)^{1/p} \end{equation} und für $p=\infty$: \begin{equation}\label{allgeq1a}\tag{ALG2} \norm f_\infty\colon=\inf\{s>0:\l(|f|>s)=0\}~. \end{equation} Dann ist $L_p(\TT)$ mit der Norm $\norm{.}_p$ ein Banachraum und für $p=2$ ein Hilbertraum mit dem inneren Produkt \begin{equation}\label{allgeq2}\tag{ALG3} \la f,g\ra\colon=\frac1{2\pi}\int f(t)\cl{g(t)}\,dt~. \end{equation} Für $p\leq q$ gilt: $\norm f_p\leq\norm f_q$ und für $f\in L_\infty(\TT)$: $\norm f_\infty=\lim_{p\to\infty}\norm f_p$. Die Menge der stetigen bzw. glatten $2\pi$-periodischen Funktionen bezeichnen wir mit $C(\TT)$ bzw. $C^\infty(\TT)$. Falls $f\in C(\TT)$, dann gilt $\norm f_\infty=\sup\{|f(\theta)|:\theta\in\TT\}$; ferner ist $C^\infty(\TT)$ für alle $1\leq p < \infty$ ein dichter Unterraum von $L_p(\TT)$; für $p=\infty$ ist $C^\infty(\TT)$ zwar dicht in $C(\TT)$ aber nicht in $L_\infty(\TT)$! Für $n\in\Z$ bezeichnen wir im weiteren mit $e_n$ die Abbildung $t\mapsto e^{int}$. Der von den Funktionen $e_n$, $n\in\Z$, erzeugte Unterraum ${\cal A}$ bildet eine Unteralgebra von $C(\TT)$ mit den Eigenschaften: $1\in{\cal A}$ und aus $T\in{\cal A}$ folgt: $\bar T\in{\cal A}$. Nach dem Stone-Weierstraß bzw. dem Nachbin Theorem, cf. e.g. wikipedia, ist ${\cal A}$ dicht in dem Banachraum $C(\TT)$ bzw. dem Fréchetraum $C^\infty(\TT)$. Da $C(\TT)$ (oder auch $C^\infty(\TT)$) wiederum dicht liegt in den Räumen $L_p(\TT)$, $1\leq p<\infty$, ist ${\cal A}$ ein dichter Unterraum von $L_p(\TT)$, $1\leq p<\infty$. Man nennt ${\cal A}$ die Menge der trigonometrisches Polynom; für $m\in\N_0$ heißt der von den Funktionen $e_n,|n|\leq m$ erzeugte Unterraum ${\cal A}_m$ der Raum der trigonometrischen Polynome des Grades $\leq m$. Da insbesondere die Folge $e_n$, $n\in\Z$, in $L_2(\TT)$ paarweise orthonormal ist, bildet sie eine orthonormale Basis von $L_2(\TT)$. Ist $1\leq q\leq\infty$, so daß $1/p+1/q=1$, dann gilt \begin{equation}\label{allgeq3}\tag{ALG4} \norm f_p=\sup\Big\{\frac1{2\pi}\Big|\int f(t)g(t)\,dt\Big|: \norm g_q\leq1, g\in{\cal A}\Big\}~. \end{equation} Sei $1\leq p<\infty$ und $1/p+1/q=1$, dann ist $L_q(\TT)$ der Dualraum von $L_p(\TT)$, d.h. zu jedem stetigen linearen Funktional $x^*:L_p(\TT)\rar\C$ gibt es genau eine Funktion $g\in L_q(\TT)$, so daß für alle $f\in L_p(\TT)$: $$ x^*(f)=\frac1{2\pi}\int fg\,d\l \quad\mbox{und}\quad \norm{x^*}=\norm g_q~. $$ Mit $\B(\TT)$ bezeichnen wir die Borelmengen von $\TT$ und mit $M(\TT)$ den Raum aller beschränkten, komplexwertigen Borelmaße auf $\TT$. $M(\TT)$ ist dann mit der sogenannten Variationsnorm \begin{equation}\label{allgeq4}\tag{ALG5} \forall\mu\in M(\TT):\qquad \norm\mu\colon=\frac1{2\pi}|\mu|(\TT) =\sup\Big\{\frac1{2\pi}\Big|\int f\,d\mu\Big|:f\in C(\TT),\norm f_\infty\leq1\Big\}~. \end{equation} ein Banachraum. Der Darstellungssatz von Riesz besagt, daß $M(\TT)$ der Dualraum von $C(\TT)$ ist, d.h. zu jedem stetigen linearen Funktional $x^*:C(T)\rar\C$ gibt es genau ein $\mu\in M(\TT)$, so daß für alle $f\in C(\TT)$: $$ x^*(f)=\int f\,d\mu \quad\mbox{und}\quad \norm{x^*}=\norm\mu~. $$
Begründen Sie \eqref{allgeq3} für $p=1$.
Sei $\mu\in M(\TT)$ mit der Verteilungsfunktion $F(\theta)\colon= \mu(-\pi,\theta]$. Falls $\mu\ll\l$, dann nennen wir $F$ absolut stetig mit der Dichte (oder Ableitung) $F^\prime\colon=d\mu/d\l\in L_1(\TT)$. Nach einem Satz von Lebesgue gilt für $\l$-fast alle $\theta\in\TT$: $$ F^\prime(\theta)=\lim_{t\to0}\frac{F(\theta+t)-F(\theta)}t~. $$ Sind $X,Y$ Banachräume und $u:X\rar Y$ ein stetiger linearer Operator, dann ist durch $$ u^*(y^*)(x)\colon=y^*(u(x)) $$ ein stetiger linearer Operator $u^*:Y^*\rar X^*$ definiert; $u^*$ heißt der zu $u$ adjungierte Operator.
Sei $p_n$, $n\in\N_0$, eine orthonormale Basis von $L_2(\O,\mu)$. Dann ist die durch $$ P_n(f) \colon=\int K_n(x,y)f(y)\,\mu(dy) \quad\mbox{mit}\quad K_n(x,y)\colon=\sum_{j=0}^n p_j(x)\cl{p_j(y)} $$ definierte lineare Abbildung die orthogonale Projektion auf den von $p_0,\ldots,p_n$ erzeugten Unterraum $E_n$. Für Polynome $p_n$ gilt die Christoffel-Darboux Formel für die Kerne $K_n(x,y)$.

Die Fouriertransformation auf dem Torus

Jede kompakte Untergruppe der multiplikativen Gruppe $\C\sm\{0\}$ ist eine Untergruppe von $\TT$.
Da $G$ kompakt ist, gibt es ein $\d > 0$, so daß für alle $z\in G$: $\d<|z| < 1/\d$. Da für alle $n\in\Z$ und alle $z\in G$: $z^n\in G$ und $|z^n|=|z|^n$, folgt: $|z|=1$.
Jede kompakte echte Untergruppe von $\TT$ ist isomorph zu $\Z_n$ für ein $n\in\N$.
Sei $\d\colon=\inf\{|t|:t\in G\sm\{0\}\}$. Falls $\d=0$, dann ist $G$ dicht in $\TT$, also $G=\TT$. Es muß also gelten $\d > 0$ und damit gilt für alle $t,\theta\in G$ mit $t\neq\theta$: $|t-\theta|\geq\d$, i.e. $G$ ist diskret und damit endlich.
Jede unendliche Untergruppe $G$ von $\TT$ ist dicht in $\TT$.
Sei $a=2\pi r$ mit irrationalem $r\in(0,1)$. Dann ist die Menge $\{na(\modul 2\pi):n\in\Z\}$ dicht in $\TT$.
Sei $\chi$ ein stetiger Homomorphismus von $\TT$ in die multiplikative Gruppe $\C\sm\{0\}$ - eine solche Funktion nennt man einen Charakter auf $\TT$. Dann gibt es ein $n\in\Z$, so daß $\chi(t)=e^{int}$.
$\proof$ Da $\TT$ kompakt ist, folgt $0<\d\leq|\chi(t)|\leq1/\d<\infty$ und damit für alle $n\in\Z$: $\d\leq|\chi(t)|^n=|\chi(nt)|\leq1/\d$, d.h. für alle $t\in\TT$ gilt: $|\chi(t)|=1$. Sei $r\in(0,1)$ irrational und $\chi(2\pi r)=e^{2\pi ixr}$ mit $x\in\R$, dann liegt die Menge $2\pi rk$, $k\in\Z$, dicht in $\TT$ und es gilt $\chi(2\pi rk)=\chi(2\pi r)^k=e^{2\pi rkix}$. Wähle $k_m\in\N$, so daß $2\pi rk_m$ in $\TT$ gegen $2\pi$ konvergiert, dann folgt: $$ e^{2\pi ix} =\lim_me^{2\pi ixrk_m} =\lim_m\chi(2\pi rk_m) =\chi(2\pi) =1 $$ und damit: $x=n\in\Z$. Für alle $k\in\Z$ erhalten wir also: $\chi(2\pi rk)=e^{2\pi inrk}$ und da $\chi$ stetig und $2\pi rk$, $k\in\Z$, dicht in $\TT$ ist, folgt für alle $t\in\TT$: $\chi(t)=e^{int}$. $\eofproof$
Bemerkung: Ist $G$ eine kommutative (topologische) Gruppe, so nennt man jeden (stetigen) Homomorphismus $\chi:G\rar S^1$ einen Charakter auf $G$. Die Menge der Charaktere bildet dann ihrerseits mit der punktweisen Multiplikation von Funktionen eine kommutative Gruppe; man nennt sie die duale Gruppe $\wh G$ von $G$. Ist z.B. $\chi:\R^d\rar S^1$ ein Charakter, so gibt es ein $y\in\R^d$, so daß für alle $x\in\R^d$: $\chi(x)=e^{i\la x,y\ra}$ - $\la.,.\ra$ bezeichnet hierin das kanonische innere Produkt auf $\R^d$ (siehe Übungen). Die duale Gruppe von $\R^d$ ist also isomorph zu $\R^d$. Cf. Harmonische Analysis auf kommutativen lokalkompakten Gruppen.
Ist $\chi:\TT^d\rar S^1$ ein Charakter, dann gibt es ein $n\in\Z^d$, so daß für alle $x\in\TT^d$: $\chi(x)=e^{i\la x,n\ra}$. $\wh \TT^d$ ist also zu $\Z^d$ isomorph.
Seien $d,p\in\N$, $p\geq2$, dann gibt es zu jedem Charakter $\chi$ auf $\Z_p^d$ ein $y\in\Z_p^d$, so daß für alle $x\in\Z_p^d$: $\chi(x)=e^{2\pi i\la x,y\ra/p}$. $\wh\Z_p^d$ ist also zu $\Z_p^d$ isomorph.
Sei $\Z_2=\{-1,1\}$ mit der Multiplikation als Gruppenoperation. Ferner sei $\P$ das Produktmaß des Maßes $\mu_1\colon=\frac12(\d_{-1}+\d_{+1})$ auf $\Z_2^\N$. Für jede endliche Teilmenge $A$ von $\N$ sei $$ \forall \o\in\Z_2^\N:\qquad w_A(\o)\colon=\prod_{j\in A}\o_j, \qquad w_\emptyset\colon=1~. $$ Zeigen Sie, daß die Funktionen $w_A$, $A\sbe\N$, $|A|<\infty$, die Charaktere von $\Z_2^\N$ sind und daß sie eine orthonormale Basis von $L_2(\Z_2^\N,\P)$ bilden. Man nennt $w_A$ die Walsh Funktionen und $X_n\colon=w_{\{n\}}$ die Rademacherfunktionen auf $\Z_2^\N$. 2. $X_n$ ist eine Folge von unabhängigen Zufallsvariablen mit $\P(X_n=1)=\P(X_n=-1)=1/2$.
Zu jedem Charakter $\chi$ auf $\Z^d$ gibt es ein $y\in\TT^d$, so daß für alle $n\in\Z^d$: $\chi(x)=e^{i\la x,y\ra}$. $\wh\Z^d$ ist also zu $\TT^d$ isomorph.
Für $f\in L_1(\TT)$, heißt die durch $$ \F(f)(n)\colon=\wh f(n)\colon=\frac1{2\pi}\int f(t)e^{-int}\,dt $$ definierte Funktion $\wh f:\Z\rar\C$ die Fouriertransformierte von $f$. $\wh f(n)$ nennt man den $n$-ten Fourierkoeffizienten von $f$ und die formale Reihe $\sum_{n\in\Z}\wh f(n)e^{int}$ die Fourierreihe $S(f)(t)$ von $f$.
Sei $t\in\TT$; die durch $L_t f(\theta)\colon=f(\theta-t)$ definierte Familie von Operatoren $L_t:L_1(\TT)\rar L_1(\TT)$ nennt man die Translationsoperatoren; sie bilden eine Gruppe, d.h. es gilt $L_tL_\t=L_{t+\t}$. Bezeichnen wir ferner die Charaktere auf $\TT$ mit $e_n$, $n\in\Z$, also $e_n(\theta)=e^{in\theta}$ und mit $\bar f$ die Funktion $\theta\mapsto\cl{f(\theta)}$, dann gilt:
\begin{equation}\label{ftoruseq0}\tag{FTT1} \wh{e_mf}(n)=\wh f(n-m),\quad \wh{\bar f}(n)=\cl{\wh f(-n)},\quad \wh{L_\theta f}(n)=e^{-in\theta}\wh f(n)~. \end{equation}
Für $f\in L_2(\TT)$ ist $\wh f(n)=\la f,e_n\ra$; die Fourierreihe ist in disem Fall die Darstellung von $f$ bezüglich der orthonormalen Basis $e_n$, $n\in\Z$. Die Parsevalsche Gleichung \begin{equation}\label{ftoruseq1}\tag{FTT2} \forall f,g\in L_2(\TT):\qquad \la f,g\ra=\sum_{n\in\Z}\wh f(n)\cl{\wh g(n)} \end{equation} besagt, daß die Fouriertransformation $\F$ eine Isometrie von $L_2(\TT)$ auf den Hilbertraum $$ \ell_2(\Z)\colon=\Big\{a:\Z\rar\C:\,\sum_{n\in\Z}|a(n)|^2<\infty\Big\} \quad\mbox{ist.} $$ Die zu $\F:L_2(\TT)\rar\ell_2(\Z)$ adjungierte Abbildung ist gegeben durch $$ \F^*(a)=\sum_{n\in\Z}a(n)e_n, $$ d.h. die adjungierte Abbildung ist die inverse, also: $\F^*=\F^{-1}$.
Bestimmen Sie die zu $L_t:L_1(\TT)\rar L_1(\TT)$ duale Abbildung.
Sei $f\in L_2(\TT)$ und $E$ der von den Funktionen $L_tf$, $t\in\TT$ aufgespannte Unterraum. Falls für alle $n\in\Z$: $\wh f(n)\neq0$, dann ist $E$ dicht in $L_2(\TT)$.
Angenommen es gibt ein $g\in L_2(\TT)$, so daß für alle $\theta\in\TT$: $\int g(t)L_\theta f(t)\,dt=0$, dann folgt nach der Parsevalsche Gleichung \eqref{ftoruseq1}: $$ \forall\theta\in\TT:\quad \sum_{n\in\Z}\wh g(n)e^{-in\theta}\wh f(n)=0 $$ Aber die Summe ist $\F^*(\wh g\wh f)(-\theta)$ und da $\F^*$ injektiv und $\wh f(n)\neq 0$ ist: $\wh g=0$, i.e. $g=0$.
Sei $f\in L_1(\TT)$, $m\in\N$ und $f_{(m)}(t)=f(mt)$. Falls $m|n$, dann gilt $\wh{f_{(m)}}(n)=\wh f(m/n)$ und andernfalls $\wh{f_{(m)}}(n)=0$.
Bestimmen Sie die Fourierkoeffizienten folgender Funktionen $f:\TT\rar\R$. 1. $f(t)=I_{(-h,h)}(t)$ mit $0 < h <\pi$. 2. $f(t)=\sign(t)$ und 3. $f(t)=t$. Suggested solution.
Zeigen Sie: $$ h\pi=\sum_{n\in\Z}n^{-2}\sin^2(nh),\quad \pi^2=4\sum_{n\in\Z}(2n+1)^{-2},\quad \pi^2=3\sum_{n\neq0}n^{-2}~. $$
Analog zu den Banachräumen $L_p(\TT)$ sind die Banachräume $\ell_p(\Z)$ definiert, als die Menge aller Funktionen $a:\Z\rar\C$, für die $\sum|a(n)|^p<\infty$; die Norm ist \begin{equation}\label{ftoruseq2}\tag{FTT3} \forall 1\leq p<\infty:\quad \norm a_p\colon=\Big(\sum_{n\in\Z}|a(n)|^p\Big)^{1/p} \end{equation} und für $p=\infty$: \begin{equation}\label{ftoruseq2a}\tag{FTT4} \norm a_\infty\colon=\sup\{|a(n)|:n\in\Z\}~. \end{equation} Schließlich definieren wir den abgeschlossenen Unterraum $c_0(\Z)$ von $\ell_\infty(\Z)$ durch \begin{equation}\label{allgeq6}\tag{FTT5} c_0(\Z)\colon=\Big\{a\in\ell_\infty(\Z):\lim_{n\to\pm\infty}a(n)=0\Big\}~. \end{equation}
Die Fouriertransformation $\F$ ist eine stetige lineare und injektive Abbildung von $L_1(\TT)$ in $c_0(\Z)$ mit dichtem Bild und $\tnorm{\F:L_1(\TT)\rar c_0(\Z)}\leq1$.
$\proof$ Da $|e_n|=1$, folgt für alle $n\in\Z$: $|\wh f(n)|\leq\norm f_1$, also $\tnorm{\F:L_1(\TT)\rar\ell_\infty(\Z)}\leq1$. Da $L_2(\TT)$ eine dichte Teilmenge von $L_1(\TT)$ ist und $\F(L_2(\TT))\sbe\ell_2(\Z)\sbe c_0(\Z)$, folgt aufgrund der Stetigkeit von $\F:L_1(\TT)\rar\ell_\infty(\Z)$ und der Abgeschlossenheit von $c_0(\Z)$ in $\ell_\infty(\Z)$: $\F(L_1(\TT))\sbe c_0(\Z)$. Falls für alle $n\in\Z$: $\wh f(n)=0$ aber $\norm f_1=1$, dann existiert nach (\ref{allgeq3}) ein trigonometrisches Polynom $T\in{\cal A}$, so daß $\norm T_\infty=1$ und $\la f,T\ra > 1/2$. $\eofproof$
Bemerkung: $\F:L_1(\TT)\rar c_0(\Z)$ ist jedoch nicht surjektiv, denn sonst wäre nach dem Open Mapping Theorem $\F$ ein Isomorphismus und damit wären auch $\ell_1(\Z)=c_0(\Z)^*$ und $L_\infty(\TT)=L_1(\TT)^*$ isomorph; $\ell_1(\Z)$ ist jedoch separabel und $L_\infty(\TT)$ ist es nicht. Cf. Banachraum Theorie.
Aus dem Interpolationssatz von Riesz-Thorin folgt:
Sei $1\leq p\leq2$ und $1/q+1/p=1$, dann ist die Fouriertransformation $\F$ eine stetige lineare Abbildung von $L_p(\TT)$ in $\ell_q(\Z)$ mit $\tnorm{\F:L_p(\TT)\rar\ell_q(\Z)}\leq1$.
Sei $f:\TT\rar\C$ absolut stetig mit $f(x)=\int_0^x f^\prime(t)\,dt$. Dann gilt für alle $n\in\Z$: $\wh{f^\prime}(n)=in\wh f(n)$. Falls ferner $f^\prime\in L_2(\TT)$ und $\int f(t)\,dt=0$, so gilt die Wirtinger Ungleichung: $\norm f_2\leq\norm{f^\prime}_2$.
$\proof$ Die erste Behauptung folgt unmittelbar mittels partieller Integration: $$ 2\pi\wh{f^\prime}(n) =\int f^\prime(t)e^{-int}\,dt =f(t)e^{-int}\Big|_{t=-\pi}^{t=\pi} +in\int f(t)e^{-int}\,dt =2\pi in\wh f(n)~. $$ Da $\F:L_2(\TT)\rar\ell_2(\Z)$ eine Isometrie ist und $\wh f(0)=\int f=0$, folgt die Ungleichung aus der ersten Behauptung. $\eofproof$
Seien $f\in L_\infty(\TT)$, $x,y\in\ell_2(\Z)$ und $$ A(x,y)\colon=\sum_{n,m\in\Z}\wh f(n+m)x_ny_m~. \mbox{ Dann gilt: } |A(x,y)|\leq\norm f_\infty\Vert x\Vert\Vert y\Vert~. $$
Es gilt mit $g(t)\colon=\sum_{n\in\Z}x_ne^{-int}$ und $h(t)\colon=\sum_{n\in\Z}y_ne^{-int}$: $$ A(x,y)=\frac1{2\pi}\int g(t)h(t)f(t)\,dt $$ Denn die rechte Seite ist gleich $$ \frac1{2\pi}\int\sum_{m,n,k}x_ny_m\wh f(k)e^{it(-n-m+k)}\,dt =\sum_{m,n}x_ny_m\wh f(m+n)~. $$ Nun ist aber $$ \frac1{2\pi}\Big|\int g(t)h(t)f(t)\,dt\Big| \leq\norm f_\infty\norm g_2\norm h_2 =\norm f_\infty\Vert x\Vert\Vert y\Vert~. $$

Dirichlet-, Fejer-, Poisson-Kern und die Hilbert-Transformation

 Sei $\sum_{n\in\Z}u_n$ eine formale Reihe mit $u_n\in\C$. Für $m\in\N_0$ und $0\leq r<1$ definiert man \begin{equation}\label{dfphkerneq1}\tag{DFP1} s_m\colon=\sum_{|n|\leq m}u_n,\quad \s_m\colon=\tfrac1{m+1}\sum_{k=0}^m s_k =\sum_{|n|\leq m}(1-\tfrac{|n|}{m+1})u_n \quad\mbox{und}\quad A(r)\colon=\sum_{n\in\Z}r^{|n|}u_n \end{equation} Die Folgen $s_m$ bzw. $\s_m$ heißen die Folge der symmmetrischen Partialsummen bzw. der Cesaro-Mittel der Folge $u_n$, $n\in\Z$. $A(r)$ nennt man in Falle der Konvergenz der Reihe das Abel-Mittel oder Poisson-Mittel der Folge $u_n$. Es gelten folgende sogenannte Abel-Sätze (cf. Analysis I):
1. Falls die Folge $s_m$ der symmetrischen Partialsummen gegen $s\in\C$ konvergiert, dann konvergiert auch die Folge $\s_m$ gegen $s$. 2. Falls die Folge der Cesaro-Mittel gegen $s\in\C$ konvergiert, dann existiert das Abel-Mittel für alle $0\leq r < 1$ und es gilt: $\lim_{r\uar1}A(r)=s$.
Das Problem der Tauber-Sätze (cf. e.g. wikipedia) ist die umgekehrte Implikation: unter welchen Voraussetzungen an die Folge $u_n$ folgt z.B. aus der Konvergenz der Abel-Mittel die Summierbarkeit der Folge?
Existiert eine Konstante $C > 0$, so daß für alle $n\in\Z$: $|nu_n|\leq C$, so folgt aus $\s_m\to s$: $s_m\to s$.

Dirichlet-Kerne

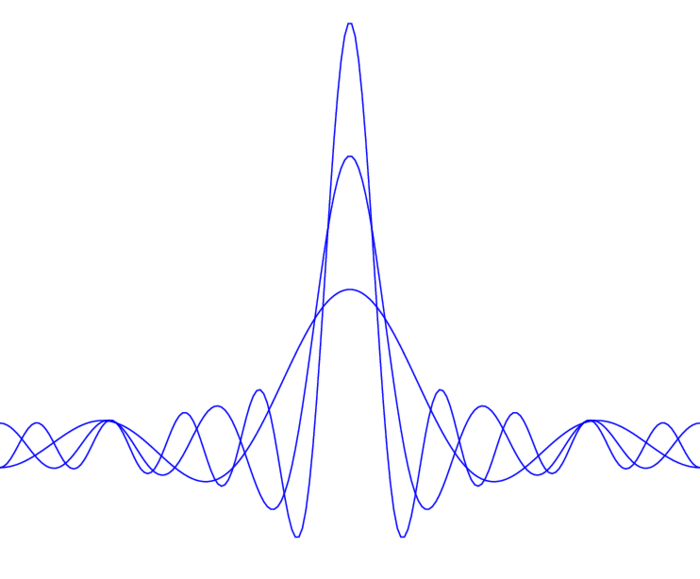
Seien $f\in L_1(\TT)$, $m\in\N_0$ und $\theta\in\TT$, dann definieren wir $$ S_m(f)(\theta)\colon=\sum_{|n|\leq m}\wh f(n)e^{in\theta} =\frac1{2\pi}\int_{-\pi}^{\pi} \Big(\sum_{|n|\leq m}e^{in(\theta-t)}\Big)f(t)\,dt =\colon\frac1{2\pi}\int_{-\pi}^{\pi}D_m(\theta-t)f(t)\,dt $$ i.e. $S_m(f)(\theta)$ ist die Folge der symmetrischen Partialsummen der Folge $\wh f(n)e^{in\theta}$; $$ D_m(t)\colon=\sum_{|n|\leq m}e^{int} $$ heißt der Dirichlet-Kern. Mittels der Summenformel für die geometrische Reihe sowie den Eulerschen Formeln folgt: \begin{equation}\label{dfphkerneq3}\tag{DFP2} D_m(t) =\frac{\sin((m+\frac12)t)}{\sin(\frac12t)} =\sin(mt)\cot(t/2)+\cos(mt) \quad\mbox{und}\quad \frac1{2\pi}\int D_m(t)\,dt=1~. \end{equation} Für $f\in L_2(\TT)$ konvergiert die Funktionenfolge $S_m(f)$ klarerweise in $L_2(\TT)$ gegen $f$, dies bedeutet jedoch nicht, daß sie punktweise konvergiert.
Die Graphen der Dirichlet-Kerne $D_m$ für $m=3,6,9$:
dirichlet
Eine Funktion $f\in L_1(\TT)$ erfülle in einem Punkt $\theta\in\TT$ die Dini-Bedingung, d.h. $$ t\mapsto\frac{f(\theta-t)-f(\theta)}t \quad\mbox{ist integrierbar.} $$ Dann gilt: $\lim_{m\to\infty}S_m(f)(\theta)=f(\theta)$; die Fourierreihe von $f$ konvergiert also im Punkt $\theta$ gegen $f(\theta)$.
$\proof$ Sei $g(t)=(f(\theta-t)-f(\theta))/t$; da $(2\pi)^{-1}\int D_m=1$, folgt: \begin{eqnarray*} \frac1{2\pi}\int_{-\pi}^\pi f(\theta-t)D_m(t)\,dt-f(\theta) &=&\frac1{2\pi}\int_{-\pi}^\pi(f(\theta-t)-f(\theta))D_m(t)\,dt\\ &=&\frac1{2\pi}\int_{-\pi}^\pi g(t)tD_m(t)\,dt\\ &=&\frac1{2\pi}\int_{-\pi}^\pi g(t)(t\cot(t/2)\sin(mt)+\cos(mt))\,dt \end{eqnarray*} $t\cot(t/2)$ ist aber auf $(-\pi,\pi]$ beschränkt, also folgt die Behauptung nach dem Riemann-Lebesgue-Lemma. $\eofproof$
Die Dini-Bedingung ist z.B. erfüllt, wenn $f:\TT\rar\C$ Lipschitz stetig ist; damit konvergiert die Fourierreihe einer Lipschitz stetigen Funktion $f$ punktweise gegen $f$.

Fejer-Kerne

Die Cesaro-Mittel sind gegeben durch \begin{equation}\label{dfphkerneq4}\tag{DFP3} \s_m(f)(\theta) \colon=\frac1{m+1}\sum_{n=0}^m S_n(f)(\theta) =\frac1{2\pi}\int_{-\pi}^{\pi}K_m(\theta-t)f(t)\,dt =\frac1{2\pi}\int_{-\pi}^{\pi}K_m(t)f(\theta-t)\,dt \end{equation} wobei $K_m(t)$ den sogenannten Fejer-Kern bezeichnet: \begin{equation}\label{dfphkerneq5}\tag{DFP4} K_m(t)\colon=\sum_{|n|\leq m}\Big(1-\frac{|n|}{m+1}\Big)e^{int} =\frac1{m+1}\Big(\frac{\sin(\frac{m+1}2t)}{\sin(\frac12t)}\Big)^2 \quad\mbox{und}\quad \frac1{2\pi}\int_{-\pi}^{\pi}K_m(t)\,dt=1~. \end{equation} Die Graphen der Fejer-Kerne $K_m$ für $m=3,6,9$: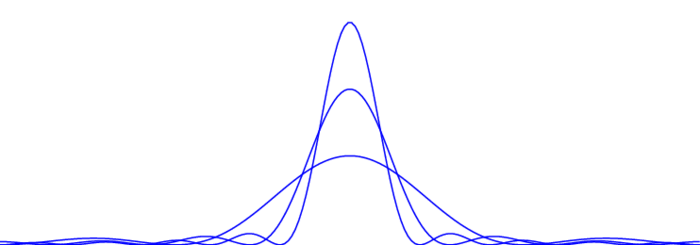
fejer
$f\in L_1(\TT)$ erfülle in $\theta\in\TT$ die sogenannte Fejer-Bedingung, d.h. der Limes $$ \lim_{t\to0}\tfrac12(f(\theta-t)+f(\theta+t)) $$ existiere. Dann gilt: $$ \lim_{m\to\infty} \s_m(f)(\theta)= \lim_{t\to0}\tfrac12(f(\theta-t)+f(\theta+t))~. $$ 2. Ist $f$ stetig, so konvergiert $\s_m(f)$ gleichmäßig gegen $f$.
$\proof$ Sei $\a=\lim_{t\to0}\tfrac12(f(\theta-t)+f(\theta+t))$; für alle $\d>0$ gilt: \begin{eqnarray*} |\s_n(f)(\theta)-\a| &=&\Big|\frac1{2\pi}\int_0^\d K_n(t)(f(\theta-t)+f(\theta+t)-2\a)\,dt\Big|\\ &&+\Big|\frac1{2\pi}\int_\d^\pi K_n(t)(f(\theta-t)+f(\theta+t)-2\a)\,dt\Big| \end{eqnarray*} Nun wählen wir zu $\e>0$ die Zahl $\d$ so klein, daß für alle $|t|<\d$: $|f(\theta-t)+f(\theta+t)-2\a|<\e$; es folgt wegen $\int K_n(t)\,dt=2\pi$ und $K_n(t)\leq\pi^2/(n+1)t^2$: $$ |\s_n(f)(\theta)-\a| \leq\e+\frac{\pi}{2\d^2(n+1)}\int_\d^\pi f(\theta-t)+f(\theta+t)-2\a\,dt $$ und damit $\limsup_n|\s_n(f)(\theta)-\a|\leq\e$.
2. Da $\TT$ kompakt ist, ist $f$ gleichmäßig stetig und somit gibt es zu jedem $\e>0$ ein $\d>0$, so daß für alle $\theta\in\TT$ und alle $|t|<\d$: $|f(\theta-t)+f(\theta+t)-2\a|<\e$. $\eofproof$
Die Indikatorfunktion der rationalen Zahlen erfüllt die Fejer-Bedingung in keinem einzigen Punkt.
Sei $\mu\in M(\TT)$ mit $\mu(\TT)=0$ und $F(\theta)\colon=\mu(0,\theta]$ - eine solche Funktion nennt man eine Funktion von beschränkter Variation. Dann gilt für alle $\theta\in\TT$: $$ \lim_{m\to\infty}S_m(F)(\theta) =\mu(-\pi,\theta]-\frac12\mu(\{\theta\}) $$ 2. Falls $\mu\ll\l$ - man nennt dann $F$ absolut stetig, konvergiert die Fourierreihe von $F_\mu$ gleichmäßig gegen $F$.
$\proof$ Aus $\mu(\TT)=0$ folgt: $F(2\pi)=0=F(0)$ und mittels partieller Integration (cf. exam) erhalten wir: $$ \int_0^{2\pi}F(t)(-ine^{-int})\,dt =F(t)e^{-int}\Big|_{0}^{2\pi}-\int_0^{2\pi}e^{-int}\,\mu(dt) =-\int_0^{2\pi}e^{-int}\,\mu(dt)~. $$ Es gilt also $|\wh F(n)|\leq C/n$. Nach Proposition, Proposition sowie der rechtsseitigen Stetigkeit von $F$ konvergiert die Fourierreihe von $F$ im Punkt $\theta$ gegen $$ \frac12(F(\theta)+F(\theta-)) =\frac12(\mu(0,\theta]+\mu(0,\theta)) =\mu(0,\theta]-\frac12\mu(\{\theta\})~. $$ $\eofproof$

Poisson-Kern und konjugierter Poisson-Kern

Die Abel-Mittel sind schließlich gegeben durch \begin{equation}\label{dfphkerneq6}\tag{DFP5} P_r(f)(\theta) \colon=\sum_{n\in\Z} r^{|n|}\wh f(n)e^{in\theta} =\frac1{2\pi}\int\Big(\sum_{n\in\Z} r^{|n|}e^{in(\theta-t)}\Big)f(t)\,dt =\frac1{2\pi}\int P(r,\theta-t)f(t)\,dt \end{equation} wobei $P(r,t)$ den sogenannten Poisson-Kern auf dem Torus bezeichnet: \begin{equation}\label{dfphkerneq7}\tag{DFP6} P(r,t) \colon=\frac{1-r^2}{1-2r\cos t+r^2} =\Re\Big(\frac{1+re^{it}}{1-re^{it}}\Big) \quad\mbox{mit}\quad \frac1{2\pi}\int P(r,t)\,dt=1~. \end{equation} Die Graphen der Poisson-Kerne $P(r,.)$ für $r=0.7,0.8,0.9$: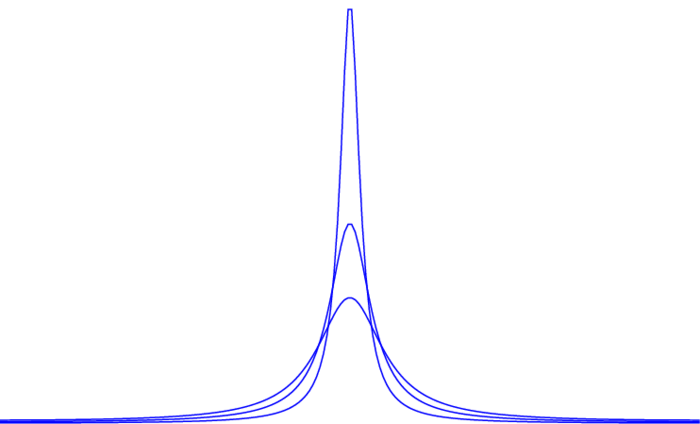
poisson
Mit $z=re^{it}$ ist also $P(r,t)$ der Realteil der auf dem offenen Einheitskreis $D\colon=\{z\in\C:|z| < 1\}$ analytischen Funktion $$ h(z) \colon=\frac{1+z}{1-z} =1+2\sum_{n=1}^\infty z^n~. $$ Somit ist für jede reellwertige Funktion $f\in L_1(\TT)$ die durch $$ u(re^{i\theta})\colon=\int P(r,\theta-t)f(t)\,dt $$ definierte Funktion $u:D\rar\R$ harmonisch. Natürlich ist diese Beziehung auch Folge des Cauchyschen Integralsatzes aus der komplexen Analysis; jedoch ist der Zusammenhang nicht ganz offensichtlich. Wir kommen in Abschnitt auf die Beziehung der beiden Formeln zurück. Hier wenden wir uns dem Imaginärteil von $h$ zu: $\Im h(re^{it})=Q(r,t)$ nennt man den konjugierten Poisson-Kern: \begin{equation}\label{dfphkerneq7kon}\tag{DFP7} \forall 0\leq r < 1\ \forall t\in\TT\qquad Q(r,t) \colon=\frac{2r\sin t}{1-2r\cos t+r^2}~. \end{equation} Die Graphen der konjugierten Poisson-Kerne $Q(r,.)$ für $r=0.7,0.8,0.9$:
conjugate poisson
Die durch $\wt u(re^{i\theta})\colon=\int Q(r,\theta-t)f(t)\,dt$ definierte Funktion $\wt u:D\rar\R$ ist gleichfalls harmonisch und $F(z)\colon=u(z)+i\wt u(z)$ ist analytisch auf $D$.
Für $r=1$ erhalten wir: $Q(1,t)=\cot(t/2)$.

Die Hilbert Transformation

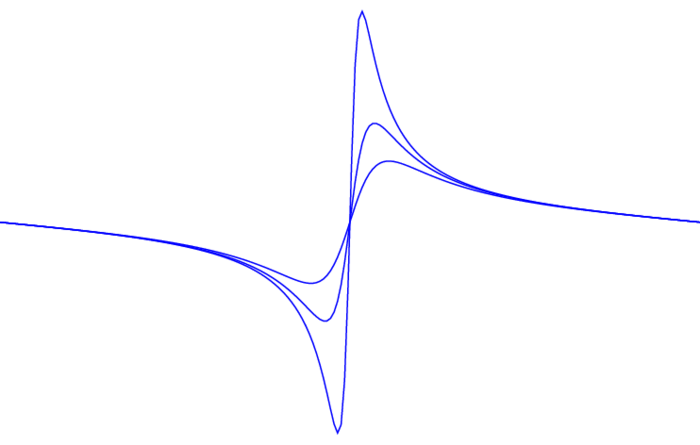
Wir bestimmen nun den Imaginärteil der Partialsummen der $h:D\rar\C$ definierenden Potenzreihe für $z=e^{it}$: zu $m\in\N_0$ sei also ($\sign(0)\colon=0$): \begin{equation}\label{dfphkerneq8}\tag{DFP8} H_m(t) \colon=\Im\Big(1+2\sum_{n=1}^m e^{int}\Big) =2\sum_{n=1}^m\sin(nt) =-i\sum_{|n|\leq m}\sign(n)e^{int} \end{equation} der Hilbert-Kern auf dem Torus; es gilt daher: $$ D_m(t)+iH_m(t)=1+2\sum_{n=1}^m e^{int}, $$ und nach der Summenformel für die geometrische Reihe sowie der Eulerschen Formel erhalten wir: \begin{equation}\label{dfphkerneq9}\tag{DFP9} H_m(t)=2\sin^2(mt/2)\cot(t/2)+\sin(mt)~. \end{equation} Schließlich definieren wir einen stetigen linearen Operator $H:L_2(\TT)\rar L_2(\TT)$: $$ \wh{Hf}(n)\colon=-i\sign(n)\wh f(n) $$ $H$ heißt die Hilbert-Transformation auf dem Torus; $H$ ist auf dem orthogonalen Komplement der konstanten Funkionen eine Isometrie in $L_2(\TT)$ und \begin{equation}\label{dfphkerneq10}\tag{DFP10} S_m(Hf)(\theta)= -i\sum_{|n|\leq m}\sign(n)\wh f(n)e^{in\theta} =\frac1{2\pi}\int_{-\pi}^\pi H_m(\theta-t)f(t)\,dt, \end{equation} Die Graphen der Hilbert-Kerne $H_m$ für $m=3,6,9$: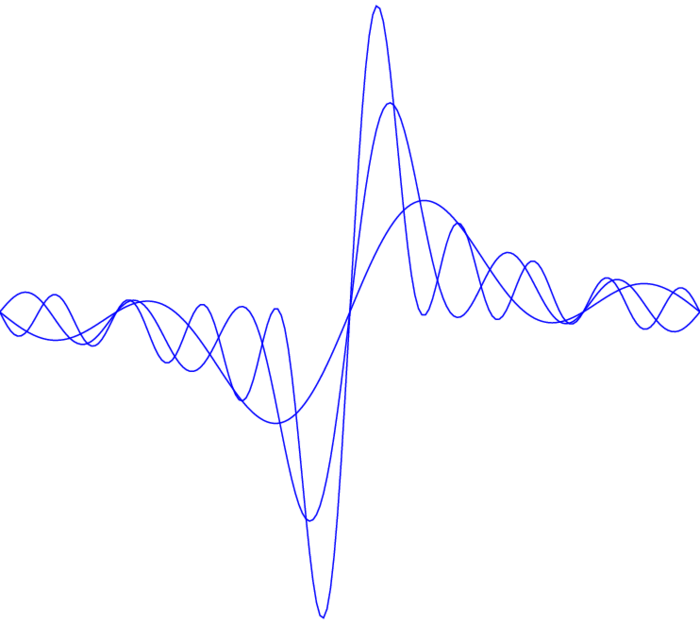
hilbert
Die Hilbert-Transformation bildet also eine Funktion $f\in L_2(\TT)$ auf eine Funktion $Hf\in L_2(\TT)$ ab und zwar so, daß wenn $u$ bzw. $\wt u$ die harmonischen Fortsetzungen von $f$ bzw. $Hf$ auf $D$ bezeichnen, die Funktion $F(z)\colon=u(z)+i\wt u(z)$ analytisch ist und $\Im F(0)=0$.
Die folgende Proposition beschreibt die Hilbert-Transformation als einen sogenannten singulären Integraloperator:
Erfüllt $f\in L_1(\TT)$ in $\theta\in\TT$ die Dini-Bedingung, dann existiert der Cauchysche Hauptwert $$ \frac1{2\pi}\pv\int f(\theta-t)\cot(t/2)\,dt \colon=\lim_{\e\dar0}\frac{1}{2\pi}\int_{|t|>\e} f(\theta-t)\cot(t/2)\,dt $$ und es gilt: $$ Hf(\theta)=\frac1{2\pi}\pv\int f(\theta-t)\cot(t/2)\,dt =\lim_{m\to\infty}S_m(Hf)(\theta)~. $$
$\proof$ Vergleiche Lemma. Analog zum Beweis von Proposition setzen wir $$ g(t)\colon=(f(\theta-t)-f(\theta+t))/t; $$ dann ist $g$ integrierbar und $$ \int_{(-r,r)^c}f(\theta-t)\cot(t/2)\,dt =\int_{r}^{\pi}g(t)t\cot(t/2)\,dt $$ also existiert der Cauchysche Hauptwert und es gilt: $$ \pv\int f(\theta-t)\cot(t/2)\,dt =\int_0^\pi g(t)t\cot(t/2)\,dt~. $$ Ferner ist für alle $r > 0$ mit $A_r=(-r,r)^c$ die Differenz $\int_{A_r}f(\theta-t)H_n(t)\,dt-\int_{A_r} f(\theta-t)\cot(t/2)\,dt$ gleich $$ \int_r^{\pi}g(t)t(H_n(t)-\cot(t/2))\,dt =\int_r^{\pi}g(t)t(-\cot(t/2)\cos(nt)+\sin(nt))\,dt~. $$ Mit $r\dar0$ folgt daher: $$ \int f(\theta-t)H_n(t)\,dt-\pv\int f(\theta-t)\cot(t/2)\,dt =\int_0^{\pi}g(t)t(-\cot(t/2)\cos(nt)+\sin(nt))\,dt $$ und mit $n\to\infty$ konvergiert dies nach dem Riemann-Lebesgue Lemma gegen $0$. $\eofproof$

Trigonometrische Reihen und das Gibbssche Phänomen

Das folgende Lemma ist ein partikulärer Fall der partiellen Integration:
Seien $z_n,w_n$, $n\in\N_0$, Folgen komplexer Zahlen und $Z_{-1}\colon=0$, $Z_n\colon=Z_{n-1}+z_n$. Dann gilt für alle $0\leq m\leq n$: $$ \sum_{k=m}^nz_kw_k =-Z_{m-1}w_m+Z_nw_{n+1}+\sum_{k=m}^nZ_k(w_k-w_{k+1})~. $$
Ist z.B. $w_n$ eine monoton fallende Folge nicht negativer Zahlen, so folgt mit $A\colon=\sup_{m-1\leq k\leq n}|Z_k|$: $$ \Big|\sum_{k=m}^n z_kw_k\Big| \leq(w_m+w_{n+1})A+\sum_{k=m}^nA(w_k-w_{k+1}) =(w_m+w_{n+1}+w_m-w_{n+1})A =2w_mA~. $$ Sind also darüber hinaus die Partialsummen $Z_n$ beschränkt und $\lim_n w_n=0$, so konvergiert die Reihe $\sum z_nw_n$.
Ist $w_n$ eine monotone Nullfolge reeller Zahlen, dann konvergiert die Reihe $\sum_{n=0}^\infty w_n\cos(nt)$ für alle $t\notin2\pi\Z$ und die Reihe $\sum_{n=0}^\infty w_n\sin(nt)$ konvergiert für alle $t\in\R$. Unklar bleibt an dieser Stelle, ob die dadurch definierte Funktion z.B. integrierbar ist!
$\proof$ Es gilt: $$ 1+2\sum_{k=1}^n\cos(kt)=D_n(t) \quad\mbox{und}\quad 2\sum_{k=1}^n\sin(kt)=H_n(t) $$ und nach \eqref{dfphkerneq3} bzw. \eqref{dfphkerneq9} gilt: $|D_n(t)|\leq\cot(t/2)+1$ bzw. $|H_n(t)|\leq2\cot(t/2)+1$. $\eofproof$
Das Gibbssche Phänomen bezieht sich auf das Verhalten einer konvergenten Fourierreihe in der Nähe einer Sprungstelle (vgl. den Dirichlet-Jordan Test, Korollar). Sei zunächst für $0\leq t\leq\pi$: $h(t)\colon=\frac12(\pi-t)$ und für $t\neq0$: $h(-t)=-h(t)$; dann folgt: $\wh h(0)=0$ und für $n\in\Z\sm\{0\}$ mittels partieller Integration: $$ \wh h(n)=\frac1{2\pi}\int_0^{\pi}h(t)(-e^{int}+e^{-int})\,dt =\frac1{i\pi}\int_0^{\pi}h(t)\sin(nt)\,dt =\frac1{2in}~. $$ Nach z.B. Proposition oder Korollar gilt für alle $\theta\in\TT\sm\{0\}$: $$ h(\theta) =\sum_{n=1}^\infty\tfrac1n\sin(n\theta) =\lim_m S_m(h)(\theta)~. $$ Aus $D_m(t)=1+2\sum_{n=1}^m\cos(nt)$ folgt: $$ \tfrac12\int_0^\theta D_m(t) =\tfrac12\theta+\sum_{n=1}^m\tfrac1n\sin(n\theta) =\tfrac12\theta+S_m(h)(\theta) $$ und damit nach (\ref{dfphkerneq3}) mit $\vp(t)=t\cot(t/2)$: \begin{eqnarray*} S_m(h)(\theta) &=&-\frac12\theta +\frac12\int_0^\theta\frac{\sin(mt)}t\vp(t)+\cos(mt)\,dt\\ &=&-\frac12\theta+\frac1m\sin(m\theta) +\frac12\int_0^\theta\frac{\sin(mt)}t\vp(t)\,dt \end{eqnarray*} Insbesondere folgt für $\theta=\pi/m$: $$ S_m(h)(\pi/m)=-\frac{\pi}{2m} +\frac12\int_0^{\pi}\frac{\sin(s)}{s}\vp(s/m)\,ds $$ und mit $m\to\infty$ erhalten wir wegen $\vp(s/m)\to2$: $$ \lim_{m\to\infty}S_m(h)(\pi/m)-h(\pi/m) =\int_0^{\pi}\frac{\sin(s)}{s}\,ds-\frac{\pi}2 \sim 0.18\pi~. $$ Ist nun $f\in L_1(\TT)$, $l>0$, $d\mu\colon=f\,d\l+l\,d\d_0$ und $F(\theta)\colon=\mu(-\pi,\theta]$, dann ist $F$ rechtsseitig stetig und $F(0)-F(0-)=l$. Ferner ist $G(t)\colon=F(t)-lh(t)/\pi$ stetig und absolutstetig; nach Korollar konvergiert daher die Fourierreihe von $G$ gleichmäßig gegen $G$, also: \begin{eqnarray*} \lim_{m\to\infty} S_m(F)(\pi/m)-F(\pi/m) &=&\lim_{m\to\infty}\frac l{\pi}(S_m(h)(\pi/m)-h(\pi/m))\\ &=&\frac l{\pi}\Big(\int_0^{\pi}\frac{\sin(s)}{s}\,ds-\tfrac12\pi\Big) \sim 0.18 l~. \end{eqnarray*} D.h. die Fourierreihe einer (rechtsstetigen) Funktion von beschränkter Variation nimmt in der Nähe einer isolierten Sprungstelle stets Werte an, die um ca. $18\%$ der Sprunghöhe über dem Funktionswert liegen. Dieses Verhalten der Fourierreihe bezeichnet man als das Gibbssche Phänomen.

Übungen und ergänzende Resultate
Sei $\vp:\R_0^+\rar\R_0^+$ stetig differenzierbar und monoton steigend mit $\vp(0)=0$. Dann gilt für alle nicht negativen $f\in L_1(\mu)$: $$ \int\vp(f)\,d\mu=\int_0^\infty\vp^\prime(t)\mu(f>t)\,dt~. $$
Nach Fubini gilt mit $A\colon=\{(t,\o):0\leq t < f(\o)\}$: \begin{eqnarray*} \int\vp(f)\,d\mu &=&\int\int_0^f\vp^\prime(t)\,dt\,d\mu =\iint\vp^\prime(t)I_A(t,\o)\,dt\,\mu(d\o)\\ &=&\int_0^\infty\int_{f > t}\vp^\prime(t)\,d\mu\,dt =\int_0^\infty\vp^\prime(t)\mu(f>t)\,dt~. \end{eqnarray*}
Seien $F,G:\R\rar\C$ von lokal beschränkter Variation und cadlag, i.e. rechtsstetig mit linksseitigen Limiten. Dann gilt für alle $x\leq y$: $$ F(y)G(y)-F(x)G(x) =\int_{(x,y]}F(t)\,dG(t)+\int_{(x,y]}G(t-)\,dF(t) $$ wobei $G(t-)\colon=\lim_{s\uar t}G(s)$. Setzen wir ferner $\D F(t)\colon=F(t)-F(t-)$, so folgt: $$ F(y)G(y)-F(x)G(x) =\int_x^yF(t-)\,dG(t)+\int_x^yG(t-)\,dF(t)+ \sum_{x < t\leq y}\D F(t)\D G(t)~. $$
Seien $\mu=\mu_F$ und $\nu=\mu_G$, dann ist nach dem Satz von Fubini mit $A\colon=(x,y]\times(x,y]$: \begin{eqnarray*} (F(y)-F(x))(G(y)-G(x)) &=&\mu\otimes\nu(A)\\ &=&\mu\otimes\nu(A\cap\{(s,t):s\leq t\}) +\mu\otimes\nu(A\cap\{(s,t):s>t\})\\ &=&\int_{(x,y]}\nu([s,y])\,\mu(ds)+\int_{(x,y]}\mu((t,y])\,\nu(dt)\\ &=&\int_{(x,y]}G(y)-G(s-)\,dF(s)+\int_{(x,y]}F(y)-F(t)\,dG(t)\\ &=&-\int_{(x,y]}G(s-)\,dF(s)-\int_{(x,y]}F(t)\,dG(t) +G(y)(F(y)-F(x))+F(y)(G(y)-G(x))~. \end{eqnarray*}
Seien $F,G:\N_0\rar\C$ mit $F(0)=G(0)=0$. Dann gilt: $$ F(n)G(n) =\sum_{k=1}^nF(k)(G(k)-G(k-1))+\sum_{k=1}^nG(k-1)(F(k)-F(k-1)) $$
Sei $c_{n+1}\geq c_n\geq c_{n-1}\geq\cdots\geq c_0\geq0$ und $p(z)\colon=\sum_{j=0}^nc_jz^j$. Dann liegen sämtliche Nullstellen in $\bar D=\{z\in\C:|z|\leq1\}$.
Sei o.B.d.A. $c_0>0$ und für $k\geq0$: $A_k=1+\cdots+z^k=(z^{k+1}-1)/(z-1)$. Dann gilt: \begin{eqnarray*} p(z) &=&\sum_{j=0}^nc_jz^j =A_nc_{n+1}-\sum_{j=0}^nA_j(c_{j+1}-c_j)\\ &=&\Big((z^{n+1}-1)c_{n+1}-\sum_{j=0}^n(z^{j+1}-1)(c_{j+1}-c_j)\Big)(1-z)^{-1}\\ &=&\Big(z^{n+1}c_{n+1}-\sum_{j=0}^nz^{j+1}(c_{j+1}-c_j)-c_0 \Big)(1-z)^{-1} \end{eqnarray*} Damit folgt für $|z|>1$: \begin{eqnarray*} |p(z)||z-1| &\geq&|z^{n+1}|c_{n+1}-\sum_{j=0}^n|z^{j+1}|(c_{j+1}-c_j)-c_0\\ &\geq&|z^{n+1}|c_{n+1}-(c_{n+1}-c_0)\sup_{0\leq j\leq n}|z^{j+1}|-c_0 \geq(|z^{n+1}|-1)c_0>0 \end{eqnarray*}
Sei $\sum_{n\geq0}c_kz^k$ eine Potenzreihe mit dem Konvergenzradius $1$, so daß $\sum_{n\geq0}c_k$ gegen $A_0$ konvergiert. Sind dann $z_1,z_2\in D$, so konvergiert die Potenzreihe auf dem von $z_1,z_2$ und $1$ erzeugten kompakten Dreieck $\D$ gleichmäßig.
Es genügt zu zeigen, daß zu jedem $\e > 0$ ein $\d > 0$ existiert, so daß für alle $z\in B_\d(1)$: $$ \Big|\sum_{k\geq 0}c_kz^k-A_0\Big|<\e~. $$ Zu $n\in\N_0$ sei $A_n\colon=\sum_{k\geq n}c_k$, dann ist $c_k=A_k-A_{k+1}$ und $A_k\to0$, also ist $M_n\colon=\sup_{k\geq n}|A_k|$ eine monotone Nullfolge und insbesondere besitzt die Potenzreihe $\sum A_kz^k$ den Konvergenzradius $1$. Für alle $z\in D$ gilt dann: \begin{eqnarray*} \sum_{k\geq 0}c_kz^k &=&\sum_{k\geq 0}(A_k-A_{k+1})z^k =\sum_{k\geq 0}A_kz^k-z^{-1}\sum_{k\geq 1}A_kz^k\\ &=&(1-1/z)\sum_{k\geq 1}A_kz^k+A_0 \end{eqnarray*} Also: $|z(\sum_{k\geq 0}c_kz^k-A_0)|=|1-z||\sum_{k\geq 1}A_kz^k|$. Nun ist für alle $m\in\N$: $$ |1-z||\sum_{k\geq 1}A_kz^k| \leq|1-z||\sum_{k=1}^mA_kz^k|+M_{m+1}|1-z|(1-|z|)^{-1} $$ Für $z\in\D$ gilt aber $|1-z|(1-|z|)^{-1}\leq C$ und $$ |1-z||\sum_{k=1}^mA_kz^k| \leq|1-z|\sum_{k=1}^m|A_k|~. $$ Sei $\e>0$; wir wählen zunächst $m\in\N$, so daß $M_{m+1}<\e$ und dann wählen wir $\d > 0$, so daß $\d\sum_{k=1}^m|A_k|<\e$. Dann folgt für alle $z\in B_\d(1)$: $$ |1-z||\sum_{k\geq 1}A_kz^k|<(1+C)\e~. $$
Verifizieren Sie die Umrechnungsformeln zwischen reeller, komplexer und physikalischer Darstellung einer trigonometrischen Reihe $$ \sum_{n\in\Z} c_ne^{int} =\tfrac12a_0+\sum_{n\in\N}a_n\cos(nt)+b_n\sin(nt) =\tfrac12a_0+\sum_{n\in\N}\r_n\cos(nt+\vp_n) $$ wobei für alle $n\in\N_0$ gilt: $$ a_n=c_n+c_{-n}=\frac1\pi\int_{-\pi}^{\pi} f(t)\cos(nt)\,dt,\quad b_n=i(c_n-c_{-n})=\frac1\pi\int_{-\pi}^{\pi} f(t)\sin(nt)\,dt $$ und $\r_n=\sqrt{a_n^2+b_n^2}$ sowie $\cos\vp_n=a_n/\r_n$, $\sin\vp_n=-b_n/\r_n$.
Sei $f\in L_2(\TT)$, dann gilt: $$ \norm{\Re f}_2^2-\Re\wh f(0)^2 =\norm{\Im f}_2^2-\Im\wh f(0)^2 =\tfrac12\sum_{n\neq0}|\Re\wh f(n)|^2+|\Im\wh f(n)|^2 $$
Es gilt mit $a(n)\colon=\Re\wh f(n)$ und $b(n)\colon=\Im\wh f(n)$: $$ \wh f(n)e^{int} =a(n)\cos(nt)-b(n)\sin(nt) +i(a(n)\sin(nt)+b(n)\cos(nt)) $$ Also: \begin{eqnarray*} \Re f(t)-a(0)&=&\sum_{n\neq0} a(n)\cos(nt)-b(n)\sin(nt)\\ \Im f(t)-b(0)&=&\sum_{n\neq0} a(n)\sin(nt)+a(n)\sin(nt) \end{eqnarray*} und damit: $$ \norm{\Re f-a(0)}_2^2 =\tfrac12\sum_n a(n)^2+b(n)^2 =\norm{\Im f-a(0)}_2^2 $$
Sei $\chi:\R\rar S^1$ ein meßbarer Homomorphismus, dann gibt es ein $y\in\R$, so daß für alle $x\in\R$: $\chi(x)=e^{ixy}$.
Sei $F(x)\colon=\int_0^x\chi(t)\,dt$, dann gilt: $$ F(x+h)=F(x)+\int_x^{x+h}\chi(t)\,dt =F(x)+\chi(x)F(h) $$ Falls für alle $h\in\R$: $F(h)=0$, dann folgt $\chi=0$ f.ü., was unmöglich ist. Sei also $h_0\in\R$, so daß $F(h_0)\neq0$, dann folgt für alle $x\in\R$: $\chi(x)=(F(x+h_0)-F(x))/F(h_0)$, i.e. $\chi$ ist stetig und folglich ist $F$ stetig differenzierbar, also ist auch $\chi$ stetig differenzierbar usw. $\chi$ ist also glatt. Aus $\chi(x+h)-\chi(x)=\chi(x)(\chi(h)-\chi(0))$ folgt nun: $\chi^\prime(x)=\chi(x)\chi^\prime(0)$, i.e. $\chi(x)=\exp(x\chi^\prime(0))$. Schließlich folgt aus $|\chi(x)|=1$: $\chi^\prime(0)=iy$ mit $y\in\R$.
Sei $\chi:\R^d\rar S^1$ ein Charakter, dann gibt es ein $y\in\R^d$, so daß für alle $x\in\R^d$: $\chi(x)=e^{i\la x,y\ra}$. $\wh \R^d$ ist also zu $\R^d$ isomorph. 2. Ist $\chi:\TT^d\rar S^1$ ein Charakter, dann gibt es ein $n\in\Z^d$, so daß für alle $x\in\TT^d$: $\chi(x)=e^{i\la x,n\ra}$. $\wh \TT^d$ ist also zu $\Z^d$ isomorph.
Für alle $j=1,\ldots,d$ sei $\chi_j(x_j)\colon=\chi(x_1,x_2,\ldots,x_d)$, dann folgt: $$ \chi(x) =\chi(x_1,\ldots,x_d) =\chi_1(x_1)\cdots\chi_d(x_d) =e^{ix_1y_1}\cdots e^{ix_dy_d} =e^{i\la x,y\ra}~. $$ 2. In diesem Fall muß für alle $m\in\Z^d$ gelten $\chi(x+2\pi m)=\chi(x)$, also für alle $m\in\Z^d$:$\la m,y\ra\in\Z$; i.e. $y\in\Z^d$.
Sei $G$ eine Gruppe mit dem neutralen Element $e$, dann ist $G^{(\N)}$ die Menge aller $(g_n)\in G^\N$, so daß $\{n\in\N:g_n\neq e\}$ endlich ist. $G^{(\N)}$ ist eine Untergruppe von $G^\N$. Sei $p\geq2$, dann gibt es zu jedem Charakter $\chi$ auf $\Z_p^\N$ ein $y\in\Z_p^{(\N)}$, so daß} für alle $x\in\Z_p^\N$: $\chi(x)=e^{2\pi i\la x,y\ra/p}$. $\wh\Z_p^\N$ ist also zu $\Z_p^{(\N)}$ isomorph.
Sei $r:\R^+\rar\R$ die Funktion $r(t)=+1$ falls $0 < t\leq 1/2$, $r(t)=-1$ falls $1/2 < t\leq1$ und $r(1+t)=r(t)$. Das System der Rademacher Funktionen $r_n:(0,1]\rar\R$ ist definiert durch $r_n(t)\colon=r(2^nt)$. Das System der Walsh Funktionen $w_n:(0,1]\rar\R$ ist nun folgendermaßen definiert: $w_0(t)\colon=1$. Ist $n\in\N$ und $n=\sum_{j\geq0}\e_j2^j$, $\e_j\in\{0,1\}$ die dyadische Darstellung von $n$, so sei $$ w_n(t)\colon=\prod_{j:\e_j=1}r_j(t) \quad\mbox{mit}\quad \prod_\emptyset\colon=1~. $$ 1. Wie hängt die Walsh Funktionen $w_n$ mit der Walsh Funktion $w_A$ des vorangehenden Beispiels zusammen? 2. Skizzieren Sie die Graphen der Funktionen $r_0,r_1,r_2,r_3$ und $w_0,\ldots,w_7$. 3. Die Walsh Funktionen sind paarweise orthogonal in $L_2(0,1]$. 4. Die Funktionen $w_0,\ldots,w_{2^n-1}$ sind auf den dyadischen Intervallen $((k-1)/2^n,k/2^n]$, $k=1,\ldots,2^n$, konstant. 5. Die Walsh Funktionen bilden ein vollständiges Orthogonalsystem, d.h. falls $f\in L_2(0,1]$ und falls für alle $n$: $\int fw_n=0$, dann folgt: $f=0$. 6. Die Walsh-Fourierkoeffizienten der Funktion $t\mapsto e^t$ sind sämtliche von $0$ verschieden
Sei $G$ eine kommutative topologische Gruppe mit der dualen Gruppe $\wh G$. Betrachten wir $\wh G$ als Unterraum der Menge der stetigen Funktionen $C(G,S^1)$ von $G$ in $S^1$ mit der Topologie der punktweisen Konvergenz, so ist $\wh G$ eine kommutative topologische Gruppe und für alle $x\in G$ ist die Abbildung $J:\chi\mapsto\chi(x)$ ein Charakter auf $\wh G$, d.h. $G$ ist eine Untergruppe der bi-dualen Gruppe. Ist $G$ eine lokalkompakte kommutative Gruppe, so ist $J$ nach dem Satz von Pontryagin ein Isomorphismus. Cf. {\em Harmonische Analysis auf kommutativen, lokalkompakten Gruppen}
Sei $f\in L_1(\TT)$ und $\vp_n$ eine Folge in $\TT$. Zeigen Sie: \begin{eqnarray*} &&\lim_n\int f(t)\cos(nt+\vp_n)\,dt=0\quad\mbox{und}\\ &&\lim_{n\to\infty}\int\sin^2(nt+\vp_n)f(t)\,dt =\lim_{n\to\infty}\int\cos^2(nt+\vp_n)f(t)\,dt =\tfrac12\int f(t)\,dt~. \end{eqnarray*}
Die Aussagen folgen aus $\cos(nt+\vp_n)=\cos(nt)\cos(\vp_n)- \sin(nt)\sin(\vp_n)$, $\cos^2(t)=(1+\cos(2t))/2$, $\sin^2(t)=(1-\cos(2t))/2$ sowie dem Riemann-Lebesgue Lemma.
Sei $A$ eine meßbare Teilmenge von $\TT$ mit $\l(A) > 0$. Konvergiert die trigonometrische Reihe $\sum a_n\cos(nt)+b_n\sin(nt)$ für alle $t\in A$, so gilt: $a_n\to0$ und $b_n\to 0$.
Sei $r_n=(a_n^2+b_n^2)^{1/2}$, dann folgt mit geeigneten $\vp_n\in\TT$: $$ a_n\cos(nt)+b_n\sin(nt)=r_n\cos(nt+\vp_n) $$ Falls $r_n$ nicht gegen $0$ konvergiert, dann gibt es ein $\e>0$ und eine Teilfolge $n(k)$, so daß $r_{n(k)}>\e$ und folglich $\cos(n(k)t+\vp_{n(k)})\to0$. Andererseits gilt nach Beispiel: $$ \lim_k\int_A\cos^2(n(k)t+\vp_{n(k)})\,dt=\tfrac12\l(A)~. $$
Konvergiert die Reihe $\sum a_n\cos(nt)+b_n\sin(nt)$ für alle $t\in A$ mit $\l(A) > 0$ absolut, so gilt: $\sum|a_n|+|b_n| < \infty$.
Sei wie oben $a_n\cos(nt)+b_n\sin(nt)=r_n\cos(nt+\vp_n)$, dann folgt für alle $t\in A$: $$ f(t)\colon=\sum_nr_n\cos^2(nt+\vp_n) \leq\sum_nr_n|\cos(nt+\vp_n)|\in\R_0^+~. $$ Sei $A_0\sbe A$, so daß $\l(A_0) > \l(A)/2$ und $f$ auf $A_0$ durch $M$ beschränkt ist; es folgt wiederum $$ \lim_n\int_{A_0}\cos^2(nt+\vp_n)\,dt=\tfrac12\l(A_0) $$ und somit gilt für $n\geq N$: $\int_{A_0}\cos^2(nt+\vp_n)\,dt>\l(A)/4$; also: $$ M\l(A_0) \geq\int_{A_0}f(t)\,dt \geq\sum_{n\geq N}r_n\int_{A_0}\cos^2(nt+\vp_n)\,dt \geq\tfrac14\l(A)\sum_{n\geq N} r_n $$ i.e. $\sum_{n\geq N} r_n\leq4M$.
← Index → Homogene Räume
<Home>
Last modified: Sun Feb 4 11:46:03 CET 2024