What is it about?
First of all this is not a lecture on physics: we don't care about experiments or verification of theories; on the other hand we care about what physicists usually don't care: we are going to elaborate on an algebraic structure! This course is intended for mathematicians who feel discontent with physicists way to convey mathematical structures. We rather employ the deductive method than the inductive method, which lectures on physics usually follow. Thus we do not start with observations, with the goal of finding a model explaining them. We essentially pursue Minkowski's geometrization of relativity (Space and Time), a view Einstein seemed to have rebutted for years.It's one of these educationally hard-boiled assumptions that the 'space' of our spacial perceptions is a three dimensional euclidean vector-space and that this space in no way depends on any state of an 'observer'. Eventually we'll keep the first (though dimension isn't important to us) and drop the second. This 'space of spatial perception' in principle differs from the 'space' of classical Newtonian mechanics, i.e. the space objects move in. The former involves 'local data' attached to a local observer or detector, such as the angle formed by two rays of light, which cross exactly at the instantaneous observers position. The latter more or less incorporates all these positions, hence it's the space light lives in, it comprises in particular all these points light has passed from it's source to an observer or detector. The way we perceive an object, its colors and its shape are assumed to be independent from the path of the light, it purely depends on the energy and the tangent vectors of these paths at the observers position. Thus mathematically speaking the 'local space' is modeled as a tangent space of the 'space of all positions' at a particular position. But since we are used to identifying the space of classical Newtonian mechanics with a three dimensional euclidean space, we are inclined to mix up all these 'spaces': a vector at a point (which is a tangent vector at this point) gets identified with a vector at another point (which is a tangent vector at this other point) by what is called 'parallel translation' and by singling out a particular point (the zero vector) of the Newtonian space we may also identify this space with any of its tangent spaces. Well, that's all admissible and it works just fine for our historically shaped common sense knowledge, but it's an immeasurable drawback when it comes to more advanced models. It didn't need relativity for these models to come up, simple experience suggested to replace the classical Newtonian space with Riemannian manifolds (just think of motions under certain constraints such as rolling a ball on a surface). Unlike the Newtonian case tangent spaces couldn't be identified in an obvious way and parallel transport became a central notion in Riemannian geometry, not at all as easily accessible as in the Newtonian case - cf. e.g. S. Gallot, D. Hulin, J. Lafontaine. But it takes some background knowledge in differential geometry to tackle these sort of problems - the sections 'Local Manifolds' and 'Observer Fields on Local Lorentz Manifolds' only give a glimpse of this subject and none of these sections is actually needed for the other sections. Since I want to keep things mathematically as elementary as possible, we are not out to work with manifolds, but with a single tangent space only. Consequently we simply need tools from linear algebra and not concepts originating in differential geometry. In relativity Riemannian manifolds get replaced with so called Lorentz manifolds or 'space-times', whose elements are called 'events' and not positions as in the classical case - cf. e.g. B. O'Neil. Also - and that's what we will be concerned with - the tangent spaces to these manifolds don't carry a euclidean structure, they carry a Lorentz structure, which admits some subspaces to be euclidean. One of the essential features that makes relativity so much different to Newtonian mechanics is the fact that our space of perception is no more the space relevant in theoretical physics, its only part of this. Both the Lorentz and the euclidean structure are particular cases of what is called an inner product. This will be explored in the run of the first chapter. The second chapter is about Lorentz spaces and some crucial notions from relativity. Time in Newtonian mechanics is a universal external parameter, which has nothing to do with the space objects are living in. As a consequence time differences (periods) as well as space differences (distances) are universal, i.e. statements like: 'ten seconds later' or 'the distance between two positions is 10 meters' are undoubtedly clear. That changes drastically with relativity. For a spacetime the previous statements only make sense in very specific situations, which must be described explicitly, otherwise they won't make sense. Riemannian manifolds are metric spaces but space-times are not (well, they are metrizable and there are lots of Riemannian structures on them, but that's physically irrelevant). Concerning 'space-times' you have to take this: there are no observer independent notions of spatial distance or time distance! Clearly, this change gets reflected in the structure of the tangent spaces. Classically the tangent space has merely 'space-like' features: the observers space of perception is isotropic. In Lorentz geometry the tangent space has a more subtle structure: it comprises time-like, light-like and space-like features and the observers space of perception is a 'space-like' subspace of the tangent space. Preposterous to our common sense model this subspace differs from the space of perception for a second instantaneous observer at the same event. Notably there is no obvious way to compare observations by different instantaneous observers, even at the same event. That's what the term 'relativity' refers to: it's not merely the trivial fact that velocities are relative, both the whole space of perception and the 'local time axis' are relative to an instantaneous observer. The term observer is a floating concept, but in any case it refers to something material, which acts in no way, it's manifestly passive and doesn't affect the spacetime it lives in.
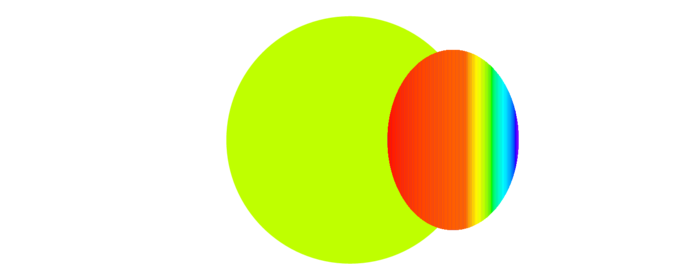
In our approach we compare instantaneous observers measurements at the same event only. Mathematically that amounts to working in a single tangent space. Since we only consider local data, i.e. data at one event, we do not have to mess with space-times but simply with vector-spaces endowed with a particular additional structure - the Lorentz product. That's why we won't elaborate on stuff like time dilation, length contraction etc., but purely on the way instantaneous observers perceive objects, their shapes and their colors. An instantaneous observer may perceive an object as a lime-colored circle and another instantaneous observer at the same event may see the same object as iridescent ellipse; all of this is not a simple function of the relative velocity of these observers, it also depends on the direction of the incident light - some objects may appear 'larger' some may appear 'smaller', some parts are red shifted some are blue shifted.
Literature
There are loads of comprehensible introductions: a pretty long list of books on the subject can be found at Zlibrary; in particular I would like to mention the introductory book Lorentz Geometry - though the goal of this book differs from our goal! Our main reference is chapter 6 in B. O'Neil's book.The domains for the Z-library online books have been seized. May be the library is still available via the Tor network! Also have a look at e.g. PDFDrive.