Linear Algebra Refreshed
This is not intended to be a basic course in linear algebra!Dual and bi-dual space
We will only consider finite dimensional vector-spaces over the reals. The dual of $E$ will be denoted by $E^*$, i.e. $E^*$ is the vector-space of all linear mappings (or linear functionals) $x^*:E\rar\R$. If $e_1,\ldots,e_n$ is a basis for $E$, then we define its dual basis $e_j^*\in E^*$ by $e_j^*(e_k)\colon=\d_{jk}$. For any $x\in E$ the numbers $e_j^*(x)$ are just the coefficents of $e_j$ in the decomposition of $x$, i.e. $$ x=\sum_j e_j^*(x)e_j~. $$ Now for all $x\in E$ the mapping $x^*\mapsto x^*(x)$ is a linear functional on $E^*$ and thus defines an element of the bi-dual $E^{**}$. $E$ and $E^{**}$ are in fact canonically isomorphic, i.e. there is an isomorphism $J:E\rar E^{**}$, which is defined without refering to any basis; indeed, define \begin{equation}\label{lareq1}\tag{LAR1} J:E\rar E^{**},\quad J(x)(x^*)\colon=x^*(x)~. \end{equation} Of course, any two finite dimensional vector-spaces of the same dimension are isomorphic, but in general we need to know bases of both spaces to define such an isomorphism. In our case $J$ is defined without refering to any basis. It is this isomorphism $J$ that allows to identify a finite dimensional vector-space with its bi-dual: if $x^{**}:E^*\rar\R$ is linear, then there is a unique $x\in E$, such that for all $x^*\in E^*$: $x^{**}(x^*)=x^*(x)$. In other words: every linear functional on $E^*$ is the evaluation at some vector $x\in E$. The benefit of this observation is that whenever a property $P$ for a finite dimensional vector-space $E$ implies a property $Q$ for its dual $E^*$, then property $P$ for $E^*$ implies property $Q$ for $E$. Given a basis $e_1,\ldots,e_n$ and its dual basis $e_1^*,\ldots,e_n^*$, we define the matrix $(a_{jk})$ of $u\in\Hom(E)$ - i.e. $u:E\rar E$ is linear - with respect to this basis by \begin{equation}\label{lareq2}\tag{LAR2} a_{jk}\colon=e_j^*(u(e_k)) \quad\mbox{i.e.}\quad u(e_k)=\sum_j a_{jk}e_j~. \end{equation} Of course, we could consider matrices of linear mappings with different domain and range and different bases for these spaces. However, we will hardly use this level of generality and thus stick to the case of linear maps $u:E\rar E$, i.e. endomorphisms, and a single basis for $E$. Anyway, here is the general definition:
Given a linear map $u:E\rar F$, bases $e_1,\ldots,e_m$ for $E$ and $f_1,\ldots,f_n$ for $F$ with dual basis $f_1^*,\ldots,f_n^*\in F^*$; the $n\times m$-matrix $A$ of $u$ with respect to these bases is given by $A\colon=(f_j^*(u(e_k))_{j,k=1}^{n,m}\in\Ma(n,m,\R)$.
Now suppose $(a_{jk})$ is the matrix of an operator $u\in\Hom(E)$ with respect to a basis $e_1,\ldots,e_n$ and $x\in E$ is an arbitary vector. Given the components $x_j\colon=e_j^*(x)$ of $x$ with respect to the basis $e_1,\ldots,e_n$, how can we compute the components $y_1,\ldots,y_n$ of $u(x)$ with respect to the basis $e_1,\ldots,e_n$? By definition these numbers are given by
$$
y_j\colon=e_j^*(u(x))
=e_j^*\Big(u\Big(\sum_k x_ke_k\Big)\Big)
=e_j^*\Big(\sum_k x_ku(e_k)\Big)
=\sum_k x_ka_{jk}
=\sum_k a_{jk}x_k
$$
and this is just the $j$-th row of an $n\times1$ matrix obtained by multiplying the matrix $(a_{jk})$ from the right with the $n\times 1$-matrix $(x_1,\ldots,x_n)^t$, i.e.
$$
\left(\begin{array}{c}
y_1\\
\vdots\\
y_n
\end{array}\right)
=\left(\begin{array}{c}
a_{11}&\cdots&a_{1n}\\
\vdots&\ddots&\vdots\\
a_{n1}&\cdots&a_{nn}
\end{array}\right)
\left(\begin{array}{c}
x_1\\
\vdots\\
x_n
\end{array}\right)
$$
By \eqref{lareq2}: $u_{jk}=e_j^*(u(e_k))=e_j^*(b_k)$ and
$$
\sum_l b_j^*(e_l)e_l^*(b_k)
=b_j^*\Big(\sum_l e_l^*(b_k)e_l\Big)
=b_j^*(b_k)
=\d_{jk}~.
$$
Analogously we get $\sum_l e_j^*(b_l)b_l^*(e_k)=\d_{jk}$.
Let $A\colon=(a_{jk})$ be the matrix of $v\in\Hom(E)$ with respect to the basis $e_1,\ldots,e_n$ and let $U$ be the matrix of exam. Then $B=(b_{jk})\colon=U^{-1}AU$ is the matrix of $v\in\Hom(E)$ with respect to the basis $b_1,\ldots,b_n$. Suggested solution.
Suppose $f,x_1^*,\ldots,x_n^*\in E^*$ such that $\bigcap\ker x_j^*\sbe\ker f$. Prove that $f$ is a linear combination of $x_1^*,\ldots,x_n^*$. Suggested solution.
Rank-Nullity Theorem
Finally let us note the well known Rank-Nullity Theorem: Suppose $u\in\Hom(E,F)$ - i.e. $u:E\rar F$ is linear - and $\dim E < \infty$, then \begin{equation}\label{lareq5}\tag{LAR5} \dim\im u+\dim\ker u=\dim E~. \end{equation} It's an obvious consequence of the Isomorphism Theorem, which states that $\im u$ is isomorphic to the quotient space $E/\ker u$ and hence $$ \dim\im u=\dim(E/\ker u)=\dim E-\dim\ker u~. $$ A unique isomorphism $\wh u:E/\ker u\rar\im u$ is given by requiring $\wh u\pi=u$, where $\pi:E\rar E/\ker u$ denotes the quotient map.An application of the Rank-Nullity Theorem is the frequently utilized fact that two subspace $F_1$ and $F_2$ of $E$ which satisfy $\dim F_1+\dim F_2 > \dim E$ have a non-trivial intersection, more precisely: $$ \dim(F_1\cap F_2)\geq\dim F_1+\dim F_2-\dim E $$ and equality holds if and only if $F_1+F_2=E$. To see this define $u:F_1\times F_2\rar E$ by $(x,y)\mapsto x+y$. By the Rank-Nullity Theorem we have: $$ \dim\ker u=\dim(F_1\times F_2)-\dim\im u \geq\dim F_1+\dim F_2-\dim E $$ with equality iff $u$ is onto, i.e. iff $F_1+F_2=E$. Obviously $\ker u=\{(x,-x):x\in F_1\cap F_2\}$ is isomorphic to $F_1\cap F_2$, i.e. $\dim\ker u=\dim(F_1\cap F_2)$.
Entire functions of an endomorphism
If $f(x)=a_0+a_1x+\cdots a_nx^n$ is a polynomial of degree $n$ and $u\in\Hom(E)$, then it's pretty clear how to define $f(u)$: $$ f(u)\colon=a_0u^0+a_1u+\cdots a_nu^n, $$ where $u^0$ is the identity, denoted by $1$ or $id$. The following definition is intended to extend the notion of a function $f(u)$ of an operator $u\in\Hom(E)$ from polynomials $f$ to entire functions $f$.
For any $u\in\Hom(E)$ the exponential $e^u\in\Hom(E)$ is defined by:
$$
\exp(u)=e^u\colon=\sum_{k=0}^\infty\frac{u^k}{k!}~.
$$
More generally, let $f:\R\rar\R$ be an entire function, i.e. the Taylor-series $\sum a_kx^k$ of $f$ at e.g. $0$ converges absolutely in all points $x\in\R$ to $f(x)$. Then we define for any $u\in\Hom(E)$:
$$
f(u)\colon=\sum_{k=0}^\infty a_ku^k~.
$$
Here we actually need some minor facts from functional analysis: $E$ with any norm is complete and thus $\Hom(E)$ with the operator norm is also complete; since the sum is absolutely convergent, the operator $f(u)$ is well defined. We won't discuss these facts, for we won't need it elsewhere. Also, by the Cayley-Hamilton Theorem
$$
f(u)=a_{n-1}u^{n-1}+\cdots+a_1u+a_0u^0,
$$
where $a_{n-1},\ldots,a_0$ are real numbers. Usually we don't write $a_0u^0$ but simply $a_0$, because it should be clear that we don't mean the real number $a_0$ but this number times the identity.Obviuously, if $A$ is the matrix of $u\in\Hom(E)$ with respect to some basis, then the exponential matrix $$ e^A\colon=\sum_{k=0}^\infty\frac{A^k}{k!} $$ is the matrix of the endomorphism $e^u$ with respect to the same basis.
The adjoint of linear mappings
Let $E,F$ be vector-spaces. The adjoint or dual of a linear mapping $u:E\rar F$ is the linear mapping $u^*:F^*\rar E^*$ defined by \begin{equation}\label{lareq3}\tag{LAR3} \forall x\in E,\,\forall y^*\in F^*:\qquad u^*(y^*)(x)=y^*(u(x))~. \end{equation} Sometimes $u^*(y^*)$ is called the pull-back of $y^*$, because $u$ maps $E$ into $F$ and $u^*$ pulls back the functional $y^*$ on $F$ to the functional $u^*(y^*)$ on $E$. Suppose $e_1,\ldots,e_n$ is a basis of $E$ with dual basis $e_1^*,\ldots,e_n^*$, then $e_j^{**}\colon=J(e_j)$ is the dual basis to $e_j^*$ (cf. exam) and thus for any linear mapping $u:E\rar E$: $$ e_j^{**}(u^*(e_k^*)) =J(e_j)(u^*(e_k^*)) =u^*(e_k^*)(e_j) =e_k^*(u(e_j)), $$ i.e. the matrix of $u^*$ with respect to the dual basis $e_1^*,\ldots,e_n^*$ is the transposed matrix of the matrix of $u$ with respect to the basis $e_1,\ldots,e_n$.
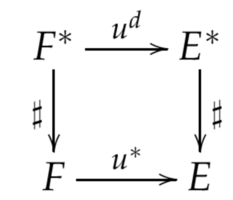
Verify that for all $u\in\Hom(E)$: $Ju=u^{**}J$ - or in diagram form:
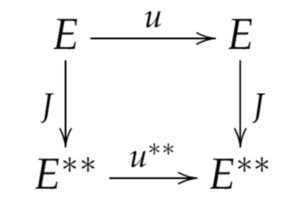Thus identifying $E$ with $E^{**}$ (via $J$), i.e. we consider $Jx$ and $x$ to be the same, we may simply write: $u^{**}=u$. Suggested solution.
Suppose $u^*(y^*)=0$ for some $y^*\in F^*\sm\{0\}$, then for all $x\in E$: $0=u^*(y^*)(x)=y^*(u(x))$, i.e. $u$ cannot be onto. Conversely if $u$ is not onto, then there is some $y^*\in F^*\sm\{0\}$, such that for all $x\in E$: $0=y^*(u(x))=u^*(y^*)(x)$, i.e. $u^*(y^*)=0$.
$\proof$
2. $(uv)^*(x^*)(x)=x^*(uv(x))=u^*(x^*)(v(x))=v^*(u^*(x^*))(x)=v^*u^*(x^*)(x)$. In particular $1=1^*=(uu^{-1})^*=u^{-1*}u^*$ and analogously $1=u^*u^{-1*}$. Since for all $n\in\N_0$: $u^{*n}=u^{n*}$ it follows (by continuity of $*$): $(e^u)^*=e^{u^*}$. 3. If $uv=vu$, then the binomial formula holds, i.e.:
$$
(u+v)^n=\sum_{k=0}^n{n\choose k}u^kv^{n-k}
$$
and therefore by rearranging terms:
$$
e^ue^v
=\sum_{k,j=0}\frac{u^kv^j}{k!j!}
=\sum_{n=0}\sum_{k=0}^n\frac{u^kv^{n-k}}{k!(n-k)!}
=\sum_{n=0}\frac1{n!}\sum_{k=0}^n{n\choose k}u^kv^{n-k}
=e^{u+v}
$$
$\eofproof$
