← Lorentz Spaces → Glossary
What should you be acquainted with? 1. Linear Algebra in particular: inner product spaces, also called spaces with a Euclidean product over the real numbers.

Tensors

Classical Examples

Classical stress tensor field

Suppose $M\sbe\R^3$ is some elastic material. For a point $m\in M$ we consider a normalized vector $N$ in the tangent space $T_mM$ of $M$ and a small surface $A$ normal to $N$. Internal strains of the material exert a force $F$ on $A$, which for small surfaces is proportional to the area $|A|$ of $A$. In general the force $F$ and the normal $N$ are not collinear. Let's assume the limit $$ S(N)\colon=\lim_{|A|\to0}\frac{F}{|A|} $$ exists at every point $m\in M$. Hence the force exerted at a surface $A$ with unit normal $N$ is up to first order given by $S(N)|A|$. For $\l\geq0$ we put $S(\l N)=\l S(N)$. This way we obtain a mapping $S_m:T_mM\rar T_mM$ and for normed $N$ $S(N)$ is just the force exerted on a unit surface normal to $N$. We'd like to justify why $S$ should be linear: At equilibrium no part of the material moves at all and hence the force exerted at a surface element $A$ with unit normal $N$ and the force exerted at a surface element $A$ with unit normal $-N$ must vanish, i.e. $S(-X)=-S(X)$. Moreover, for a normalized vector $N\in T_mM$ we consider a small tetrahedral block of material with faces $A_1,A_2,A_3$ and $A$ normal to an orthonormal basis $-E^1,-E^2,-E^3$ and $N=n_1E^1+n_2E^2+n_3E^3$ for some $n_j > 0$. Again at equilibrium the sum of the forces on the faces must vanish and thus $$ S(N)|A|+S(-E^1)|A_1|+S(-E^2)|A_2|+S(-E^3)|A_3|=0~. $$ Since $|A_j|=|A|\la N,E^j\ra$, we have $|A_j|/|A|=n_j$ and therefore $$ S(N)=n_1S(E^1)+n_2S(E^2)+n_3S(E^3)~. $$ Hence $S$ must be linear.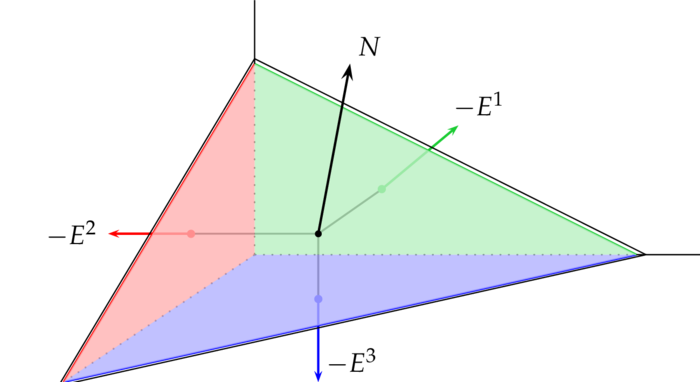
Stress tensor
Finally let's define a bi-linear map $T:T_mM\times T_mM\rar\R$ by putting for all $X,Y\in T_mM$: $$ T(X,Y)\colon=\la S(X),Y\ra~. $$ This is called the stress tensor of $M$ at $m\in M$. Doing this for every $m\in M$ we obtain what is called the stress tensor field of $M$ - of course, we assume that the dependence on $m$ is smooth! For normalized tangent vectors $X$ and $Y$ $T(X,Y)$ is just the force along $Y$ exerted on a unit surface normal to $X$. If $S(X)=P(m)X$, then the force is isotropic at $m$, i.e. it doesn't depend on the direction; in this case $P(m)$ is called the pressure at $m$.
Beware! text books in theoretical physics usually drop the term 'field' for any sort of tensor field: thus the 'stress tensor field' is simply called 'stress tensor'!

Perfect fluid

Let $M\sbe\R^3$ be a fluid and again $m\in M$ an arbitrary but fixed point. Let $V$ be the velocity of the fluid at $m$, $\r(m)$ the density of the fluid at $m$ and $P(m)$ the pressure at $m$. We define a bi-linear map $T:T_mM\times T_mM\rar\R$: $$ T(X,Y) \colon=\r(m)\la X,V\ra\la Y,V\ra+P(m)\la X,Y\ra =\la\r(m)\la X,V\ra V+P(m)X,Y\ra $$ Assuming $T$ to be a stress tensor field we get for the associated force $S(X)$ on a unit surface normal to a unit vector $X\in T_mM$: $$ S(X)=\r(m)\la X,V\ra V+P(m)X~. $$ Thus for $X\perp V$ the force is isotropic and its norm is $P$; for $X=V/\norm V$ the force acts again in the direction of $X$ but its norm is $\r\norm V^2+P$, accounting for the additional pressure of the flow.

Symmetry

Any inner product is symmetric. Also the stress tensor field of a perfect fluid is symmetric, indeed $$ T(Y,X)= \r(m)\la Y,V\ra\la X,V\ra+P(m)\la Y,X\ra =\r(m)\la X,V\ra\la Y,V\ra+P(m)\la X,Y\ra =T(X,Y)~. $$ Actually, any stress tensor should be symmetric. To show this satisfactorily we consider the moment $N$ on a small cubic block at about $m\in M$. Up to a constant factor this moment is the sum of the moments of all six faces of the cubic block; as $S$ is linear we have $S(-E^j)=-S(E^j)$ and therefore: $$ N=2\sum_{j=1}^3 E^j\times S(E^j)~. $$ At equilibrium this moment must vanish. By vector calculus we also have: $$ \la E^j\times S(E^j),X\ra =\la X\times E^j,S(E^j)\ra $$ and thus we get for e.g. $X=E^1$: \begin{eqnarray*} 0&=&\la E^1\times E^2,S(E^2)\ra+\la E^1\times E^3,S(E^3)\ra\\ &=&\la E^3,S(E^2)\ra-\la E^2,S(E^3)\ra =T(E^2,E^3)-T(E^3,E^2) \end{eqnarray*}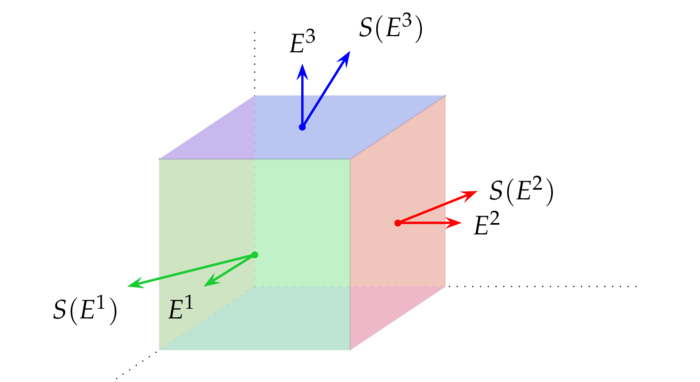
Symmetry of stress tensor

Relativistic perfect fluid

In the relativistic case we replace the Euclidean product with the Lorentz product and the velocity by an instantaneous observer $U$. Finally instead of the mass density $\r$ we take the energy density observed by $U$, which we will also denote by $\r$. Now we stipulate the following properties:
  1. If $X,Y$ are in the local rest space of the instantaneous observer $U$, i.e. $X,Y\perp U$, then $T(X,Y)$ should be the force exerted on a unit surface normal to $X$ in the direction of $Y$, i.e.: $T(X,Y)=P\la X,Y\ra$.
  2. If $X=U$, then $T(X,X)$ should be the energy density $\r$ observed by $U$, i.e. $T(U,U)=\r$.
In analogy to the classical case we try the following symmetric ansatz: $$ T(X,Y)=f\la X,U\ra\la Y,U\ra+g\la X,Y\ra~. $$ The above conditions then imply that $f=\r+P$ and $g=P$, i.e. $T$ is given by $$ T(X,Y)=(\r+P)\la X,U\ra\la Y,U\ra+P\la X,Y\ra~. $$ The vector $S(X)\colon=(\r+P)\la X,U\ra U+PX$ satisfies $\la S(X),Y\ra=T(X,Y)$ and is called the Minkowski force. If $X$ is in the rest space of $U$, then $S(X)=PX$, i.e.unlike the classical case the force for $U$ is isotropic in the rest space of $U$. That's ok, because for $U$ the fluid doesn't move at all! For another instantaneous observer $Z$ we get $T(Z,U)=-\r\la Z,U\ra$, that's the energy density observed by $Z$.

Tensors

Definition

In physics and differential geometry it's tensor fields on manifolds that are dealt with, but at a fixed point $m$ of the manifold $M$ a tensor field is simply a tensor on the tangent space $T_mM$. Hence tensors are objects of linear algebra. So what is meant by a tensor in linear algebra? Vectors, linear functionals, bi-linear mappings, inner products are particular tensors. In this section we discuss the general concept of a tensor. We will still assume all vector-spaces to be finite dimensional. So let $E$ be a finite dimensional real vector-space. Since any linear functional on $E^*$ is the evaluation at a certain vector $x\in E$, we identify as usual the bi-dual $E^{**}$ with $E$.
A $(p,q)$-tensor on a finite dimensional vector-space $E$ is a multi-linear mapping $$ A:\underbrace{E\times\cdots\times E}_p\times \underbrace{E^*\times\cdots\times E^*}_q\rar\R~. $$ The set of all $(p,q)$-tensors on $E$ will be denoted by ${\cal T}_q^p(E)$; it's a vector-space of dimension $(\dim E)^{p+q}$. In particular ${\cal T}^p(E)$ and ${\cal T}_q(E)$ are called the space of all covariant $p$-tensors and the space of all contravariant $q$-tensors.
Clearly ${\cal T}^1(E)=E^*$ and ${\cal T}_1(E)=E^{**}$, which is identified with the vector-sapce $E$. Also, instead of a single space $E$ we could have taken a tuple of vector-spaces $E_1,\ldots,E_p$. For the sake of simlicity we mostly stick to the case where all these spaces coincide.
Every vector $x\in E$ is a contravariant $1$-tensor. Every linear functional $x^*\in E^*$ is a covariant $1$-tensor and every bi-linear map $B:E\times E\rar\R$ is a covariant $2$-tensor. Defining $A$ by $A(x,x^*)\colon=x^*(x)$ we get a $(1,1)$-tensor $A$.

Bases for tensor spaces

To construct a basis for ${\cal T}^p(E)$ we first define what is called the tensor product $A\otimes B\in{\cal T}^{p+q}(E)$ of $A\in{\cal T}^p(E)$ and $B\in{\cal T}^q(E)$: \begin{equation}\label{teneq1}\tag{TEN1} A\otimes B(x_1,\ldots,x_p,y_1,\ldots.y_q)\colon= A(x_1,\ldots,x_p)B(y_1,\ldots.y_q)~ . \end{equation} The mapping $(A,B)\mapsto A\otimes B$ is bi-linear and we have: $$ A\otimes(B\otimes C)=(A\otimes B)\otimes C $$ and thus the space $$ {\cal T}(E)\colon=\bigoplus_{p=0}^\infty{\cal T}_p(E) $$ where ${\cal T}_0(E)\colon=\R$, is an algebra with unit - the (covariant) tensor algebra.
Suppose $x\in E$ and $x^*\in E^*$, the $x\otimes x$, $x\otimes x^*$, $x^*\otimes x$ and $x^*\otimes x^*$ are the bi-linear mappings $(y^*,z^*)\mapsto y^*(x)z^*(x)$, $(y^*,y)\mapsto y^*(x)x^*(y)$, $(y,z^*)\mapsto x^*(y)z^*(x)$ and $(y,z)\mapsto x^*(y)x^*(z)$.
Now if $e_j$ is a basis for $E$, then $e_{j_1}^*\otimes\cdots\otimes e_{j_p}^*$ is a basis for ${\cal T}^p(E)$ because for any $A\in{\cal T}^p(E)$ we have $$ A(x_1,\ldots,x_p) =\sum_{j_1,\ldots,j_p}A(e_{j_1},\ldots,e_{j_p})\prod_k e_{j_k}^*(x_k) =\sum_{j_1,\ldots,j_p}A(e_{j_1},\ldots,e_{j_p})e_{j_1}^*\otimes\cdots\otimes e_{j_p}^*(x_1,\ldots,x_p) $$ Hence we will also use the notation $E^*\otimes\cdots\otimes E^*$ for ${\cal T}^p(E)$. The tensor product of contravariant or mixed tensors is defined analogously and we will write $E\otimes\cdots\otimes E$ for ${\cal T}_p(E)$. More generally $E_1^*\otimes\cdots\otimes E_p^*$ will simply be another notation for the space of all $p$-linear mappings $A:E_1\times\cdots\times E_p\rar\R$. The advantage of this new notation becomes evident when discussing the so called universal property!
Let $A$ be the $(1,1)$-tensor $A(x,x^*)\colon=x^*(x)$; compute the components of $A$ with respect to the basis $e_j\otimes e_k^*$.
Since $A(e_j,e_k^*)=\d_{jk}$, it follows that $A=\sum_j e_j^*\otimes e_j$.
Every $u\in\Hom(E)$ may be viewed as $(1,1)$-tensor $A:(x,x^*)\mapsto x^*(u(x))$ and vice versa. In particular the $(1,1)$-tensor $A=b\otimes a^*$ can be identified with the linear mapping $x\mapsto a^*(x)b$.
Suppose $A$ is a $(1,1)$-tensor, then $u\in\Hom(E)$ is uniquely defined by $x^*(u(x))=A(x,x^*)$. We construct $u$ more explicitely: Suppose $e_1,\ldots,e_n$ is a basis for $E$; put $a_{jk}\colon=A(e_k,e_j^*)$ and define $u\in\Hom(E)$ by $u(x)\colon=\sum a_{jk}e_k^*(x)e_j$. Considering $b\otimes a^*$ as a linear mapping, we have: $$ u=\sum a_{jk}e_j\otimes e_k^* $$ and considering $b\otimes a^*$ as the $(1,1)$-tensor: $(x,x^*)\mapsto a^*(x)x^*(b)$, we also have $$ A=\sum a_{jk}e_j\otimes e_k^*~. $$
If $e_1,\ldots,e_n$ is a basis with dual basis $e_1^*,\ldots,e_n^*$, then: $\sum e_j^*\otimes e_j=id_E$ and $\sum e_j\otimes e_j^*=id_{E^*}$. Thus for all $u\in\Hom(E)$: $u(x)=u(\sum e_j^*(x)e_j)=\sum e_j^*(x)u(e_j)$, i.e.: $u=\sum e_j^*\otimes u(e_j)$ and analogously: $u^*=\sum e_j\otimes u^*(e_j^*)$.
Suppose $\dim E=2$ and $e_1,e_2$ is a basis for $E$. Then for $u\in\Hom(E)$ and $\o=e_1^*\otimes e_2^*-e_2^*\otimes e_1^*$ we have $\o(u(e_1),u(e_2))=\det u$.
Let $A\in{\cal T}_q^p(E)$ and $e_1,\ldots,e_n$ a basis of $E$ with dual basis $e_1^*,\ldots,e_n^*$. Often the components $A(e_{j_1},\ldots,e_{j_p},e_{k_1}^*,\ldots,e_{k_q}^*)$ are denoted by $A_{j_1,\ldots,j_p}^{k_1,\ldots,k_q}$ and the collection of all these numbers are said to form a $(p,q)$-tensor. We won't encourage that point of view, because it doesn't make sense without refering to a basis.
Suppose $e_1,\ldots,e_n$ is a basis for $E$. Prove that $$ \la.,.\ra \colon=-\sum_{j\leq\nu}e_j^*\otimes e_j^*+\sum_{j>\nu}e_j^*\otimes e_j^* $$ is an inner product on $E$ such that $\la e_j,e_k\ra=\e_j\d_{jk}$, where $\e_1=\cdots=\e_\nu=-1$ and $\e_{\nu+1}=\cdots=\e_n=1$.

The universal property

Let $A:E\times\cdots\times E\rar F$ be a $p$-linear map, then there is exactly one linear map $\wt A:E\otimes\cdots\otimes E\rar F$, such that for all $x_1,\ldots,x_p\in E$: $$ \wt A(x_1\otimes\cdots\otimes x_p)=A(x_1,\ldots,x_p)~. $$ This is called the universal property of the tensor product. Moreover the mapping $A\mapsto\wt A$ is an isomorphism. We will verify this property for $p=2$: Let $e_1,\ldots,e_n$ be a basis for $E$, then there is only one possible definition for $\wt A(e_j\otimes e_k)=A(e_j,e_k)$ and we extend $\wt A$ linearly on all of $E\otimes E$. By bi-linearity of $(x,y)\mapsto x\otimes y$ and $A$ we infer that for all $x,y\in E$: \begin{eqnarray*} \wt A(x\otimes y) &=&\wt A\Big(\sum x_je_j\otimes\sum y_ke_k\Big) =\wt A\Big(\sum x_jy_ke_j\otimes e_k\Big)\\ &=&\sum x_jy_k\wt A(e_j\otimes e_k) =\sum x_jy_kA(e_j,e_k) =A\Big(\sum x_je_j,\sum y_ke_k\Big)~. \end{eqnarray*} Finally the mapping $A\mapsto\wt A$ is linear and injective; as both spaces have the same dimension, it must be an isomorphism.
We'd like to notice that this construction only relies on the fact that the set $e_j\otimes e_k$, $1\leqj,k\leq n$, is a basis for $E\otimes E$! Thus it's not at all surprising that there is a more abstract definition of tensor products in algebra, which, in its core, is just a set of properties assuring the universal property.
The space of all $p$-linear mappings from $E_1\times\cdots\times E_p$ into $F$ is isomorphic to the space of all linear mappings from $E_1\otimes\cdots\otimes E_p$ into $F$ and this isomorphism is given by $A\mapsto\wt A$.
We mention some applications of this identification:
1. In the case $F=\R$ we can identify the dual of ${\cal T}_p(E)$ with ${\cal T}^p(E)$: for every linear functional $\wt A:{\cal T}_p(E)\rar\R$ there is exactly one $A\in{\cal T}^p(E)$, such that for all $x_1,\ldots,x_p\in E$: $$ \wt A(x_1\otimes\cdots\otimes x_p)=A(x_1,\ldots,x_p)~. $$ Using different notation: $(E\otimes\cdots\otimes E)^*=E^*\otimes\cdots\otimes E^*$. In particular we may view $A\colon=x_1^*\otimes\cdots\otimes x_p^*$ as the linear functional on ${\cal T}_p(E)$ given by $$ x_1\otimes\cdots\otimes x_p\mapsto x_1^*(x_1)\cdots x_p^*(x_p)~. $$ Analogously we may think of $B\colon=x_1\otimes\cdots\otimes x_p$ as the linear functional on ${\cal T}^p(E)$ given by $$ x_1^*\otimes\cdots\otimes x_p^*\mapsto x_1^*(x_1)\cdots x_p^*(x_p)~. $$ 2. The algebraic definition of the trace: There is exactly one linear functional $\tr:E\otimes E^*\rar\R$, such that for all $x\in E$ and all $x^*\in E^*$: $\tr(x\otimes x^*)=x^*(x)$. This follows from the fact that the mapping $(x,x^*)\rar x^*(x)$ is bi-linear and hence by the universal property there is exactly one linear map $\tr:E\otimes E^*\rar\R$ with the above property.
3. Following exam we may identify $E\otimes E^*$ with $\Hom(E)$ : just think of $x\otimes x^*$ as the linear mapping $y\mapsto x^*(y)x$. Thus the trace of the linear mapping $u\colon=\sum a_{jk}x_j\otimes x_k^*$ is $$ \sum a_{jk}\tr(x_j\otimes x_k^*)=\sum a_{jk}x_k^*(x_j)~. $$ 4. ${\cal T}^p(E)\otimes{\cal T}^p(E)$ and ${\cal T}^{p+q}(E)$ are isomorphic: the mapping ${\cal T}^p(E)\times{\cal T}^p(E)\rar{\cal T}^{p+q}(E)$, $(A,B)\mapsto A\otimes B$ is bi-linear and the corresponding linear map ${\cal T}^p(E)\otimes{\cal T}^p(E)\rar{\cal T}^{p+q}(E)$ maps a basis onto a basis, thus it's an isomorphism.
5. Suppose $u\in\Hom(E)$, $v\in\Hom(F)$. The mapping $(x,y)\mapsto u(x)\otimes v(y)$ from $E\times F$ into $E\otimes F$ is bi-linear, hence there is exactly one linear map $\wt{u\otimes v}:E\otimes F\rar E\otimes F$, such that for all $x\in E,y\in F$: $$ \wt{u\otimes v}(x\otimes y)=u(x)\otimes v(y)~. $$ Now the mapping $(u,v)\mapsto\wt{u\otimes v}$ is again bi-linear from $\Hom(E)\times\Hom(F)$ into $\Hom(E\otimes F)$ and thus there is another linear map $\Hom(E)\otimes\Hom(F)\rar\Hom(E\otimes F)$. This linear map maps $u\otimes v$ onto the linear map: $\wt{u\otimes v}$.
Verify that the map $\Hom(E)\otimes\Hom(F)\rar\Hom(E\otimes F)$ which sends $u\otimes v$ to the linear map: $\wt{u\otimes v}$ is an isomorphism.
Therefore we won't distinguish $u\otimes v$ from $\wt{u\otimes v}$ and usually regard $u\otimes v$ as the linear map on $E\otimes F$ which satisfies $$ \forall x\in E\ \forall y\in F:\quad u\otimes v(x\otimes y)=u(x)\otimes v(y)~. $$
Verify that for all $u_1,u_2\in\Hom(E)$ and all $v_1,v_2\in\Hom(F)$: $(u_1\otimes v_1)(u_2\otimes v_2)=u_1u_2\otimes v_1v_2$.
Suppose $u\in\Hom(E)$, $v\in\Hom(F)$ and $u\otimes v\in\Hom(E\otimes F)$ and let $e_j$ and $f_k$ be bases for $E$ and $F$, respectively. Verify that the matrix of $u\otimes v$ with respect to the basis $e_1\otimes f_1,e_1\otimes f_2,\ldots,e_1\otimes f_n,e_2\otimes f_1,\ldots,e_m\otimes f_n$ is given by the block matrix $$ \left(\begin{array}{cccc} a_{11}B&a_{12}B&\cdots&a_{1m}B\\ a_{21}B&a_{22}B&\cdots&a_{2m}B\\ \vdots&\vdots&\ddots&\vdots\\ a_{m1}B&a_{m2}B&\cdots&a_{mm}B \end{array}\right)~. $$ where $A$ and $B$ are the matrices of $u$ and $v$ with respect to the bases $e_1,\ldots,e_m$ and $f_1,\ldots,f_n$, respectively. Usually the matrix given above is called the Kronecker product of the matrices $A$ and $B$ and it's denoted by $A\otimes B$.
6. The mapping $(u,v)\mapsto\tr(u)v$ is bi-linear from $\Hom(E)\times\Hom(F)$ into $\Hom(F)$. By the universal property there is exactly one linear map $\tr_1:\Hom(E)\otimes\Hom(F)=\Hom(E\times F)\rar\Hom(F)$ such that $\tr_1(u\otimes v)=\tr(u)v$. $\tr_1$ is called the partial trace
7. Let $X$ be a finite set and $E=\R^X$ the space of all functions $f:X\rar\R$. Then $E\otimes E$ is isomorphic to the space of all functions $f:X^2\rar\R$ and the isomorphism is given by $J:f\otimes g\mapsto((x,y)\mapsto f(x)g(y))$: the mapping $(f,g)\mapsto((x,y)\mapsto f(x)g(y))$ is bi-linear and $J$ is the corresponding linear map; $J$ maps the basis $\d_x\otimes\d_y$, $x,y\in X$ onto a basis, i.e. $J$ is an isomorphism. Thus, identifying $f\otimes g$ with the function $(x,y)\mapsto f(x)g(y)$, we see that $E\otimes E$ coincides with the space of all functions $f:X^2\rar\R$; generalizing we have $$ \R^X\otimes\R^Y=\R^{X\times Y}~. $$ 8. Complexification: The space $\C\otimes E$ has real dimension $2\dim E$; but this space is also a complex vector-space: scalar multiplication is defined by: $a(b\otimes x)\colon=(ab)\otimes x$; the space $\C\otimes E$ is called the complexification of $E$. For $u\in\Hom(E)$ the mapping $1\otimes u\in\Hom(\C\otimes E)$ is the $\C$-linear extension, i.e. $1\otimes u(1\otimes x)=u(x)$ - usually this extension is also denoted by $u$. The $\R$-linear mapping $a\otimes x\mapsto\bar a\otimes x$ is called the conjugation.
Suppose $W$ is a complex vector-space and $E\sbe W$ is a real subspace, such that for all $x\in E\sm\{0\}$: $ix\notin E$. Then $\C\otimes E$ is isomorphic to the subspace $E+iE\colon=\{x+iy:x,y\in E\}$ of $W$ and the mapping $1\otimes x+i\otimes y\mapsto x+iy$ is an isomorphism from $\C\otimes E$ onto $E+iE$,
The space $S$ of all self-adjoint linear operators on a complex Euclidean space $E$ is a real subspace of $\Hom(E)$. Show that $\C\otimes S$ is isomorphic to $\Hom(E)$.
The space $A$ of all skew-symmetric linear operators on a complex Euclidean space $E$ is a real subspace of $\Hom(E)$. Show that $\C\otimes A$ is isomorphic to $\Hom(E)$.
Determine the complexification of $E\colon=\{A\in\Ma(n,\C): A=\bar A^t,\tr A=0\}$.

Pull-back

 The pull-back of $A\in{\cal T}^p(F)$ by $u\in\Hom(E,F)$ is the convariant tensor $u^*A\in{\cal T}^p(E)$ defined by \begin{equation}\label{teneq2}\tag{TEN2} u^*A(x_1,\ldots,x_p)\colon=A(u(x_1),\ldots,u(x_p))~. \end{equation} If $p=1$ then the pull back $y^*\mapsto u^*y^*$ coincides with the adjoint or dual map of $u$.
Verify that for all $A,B\in{\cal T}^p(F)$ and all $u\in\Hom(E,F)$: $u^*(A\otimes B)=u^*A\otimes u^*B$.
Verify that for all $u\in\Hom(E,F)$, $v\in\Hom(F,G)$ and all $A\in{\cal T}^p(G)$: $(vu)^*A=u^*v^*A$.

$(r,s)$-trace

For $A\in{\cal T}_1^1(E)$ we defined the trace $\tr A$ as the unique linear map $\tr:{\cal T}_1^1(E)\rar\R$ such that $\tr(x\otimes x^*)=x^*(x)$. Given a basis $b_1,\ldots,b_n$ for $E$ with dual $b_1^*,\ldots,b_n^*$ this amounts to $$ \tr A =\sum_jA(b_j,b_j^*) $$ and, of course, this value does not depend on the basis. Now for $1\leq r\leq p$ and $1\leq s\leq q$ we define the $(r,s)$-trace of a $(p,q)$-tensor $A$ to be the $(p-1,q-1)$-tensor: $$ \tr_{r,s}A\colon=\sum_jA(\ldots,b_j,\ldots,b_j^*,\ldots) $$ where $b_j$ is in slot $r$ and $b_j^*$ in slot $(p+s)$. Again, this value does not depend on the basis!

Contraction

The contraction of a $p$-tensor $A\in{\cal T}^p(E)$ by a vector $x\in E$ is defined to be the $(p-1)$-tensor \begin{equation}\label{teneq3}\tag{TEN3} x\contract A(x_1,\ldots,x_{p-1})\colon=A(x,x_1,\ldots,x_p)~. \end{equation} Take for example $x^*,y^*\in E^*$ and $z\in E$, then $x^*\otimes y^*\in{\cal T}^2(E)$ and $z\contract(x^*\otimes y^*)$ is the linear functional $x^*(z)y^*$. Also if $B$ is non-singular and bi-linear, then the musical isomorphism $x\mapsto x^\flat$ is given by: $x^\flat=x\contract B$.

Alternating Forms

Definition

Let $S_p$ be the group of permutations of the numbers $\{1,\ldots,p\}$; for $\s\in S_p$ and $x_1,\ldots,x_p\in E$ let $\s\cdot(x_1,\ldots,x_p)$ be the $p$-tuple $(x_{\s(1)},\ldots,x_{\s(p)})$. Putting for $\r\in S_p$: $y_j=x_{\r(j)}$ we get \begin{eqnarray*} \s\cdot(\r\cdot(x_1,\ldots,x_p)) &=&\s(x_{\r(1)},\ldots,x_{\r(p)}) =(y_{\s(1)},\ldots,y_{\s(p)})\\ &=&(x_{\r(\s(1))},\ldots,x_{\r(\s(p))}) =(\r\circ\s)\cdot(x_1,\ldots,x_p)~. \end{eqnarray*} If you mind the swapping of the permutations, you should define the operation by $$ \s\cdot(x_1,\ldots,x_p) \colon=(x_{\s^{-1}(1)},\ldots,x_{\s^{-1}(p)})~. $$ Then you have $\s\cdot(\r\cdot(x_1,\ldots,x_p))=(\s\circ\r)\cdot(x_1,\ldots,x_p)$, i.e. $S_p$ operates on $E^p$ from the left.
A covariant $p$-tensor $\o$ is said to be alternating if for all $\s\in S_p$: $$ \o\circ\s(x_1,\ldots,x_p) \colon=\o(\s\cdot(x_1,\ldots,x_p)) =\sign(\s)\o(x_1,\ldots,x_p)~. $$ An alternating $p$-tensor is also called an alternating $p$-form on $E$ or simply a $p$-form on $E$. A $1$-form is just another name for a linear functional.
For all $\pi\in S_p$ we have $\sign(\pi^{-1})=\sign(\pi)$.
We define a linear mapping $\alt:{\cal T}^p(E)\rar{\cal T}^p(E)$ by: $$ \alt A(x_1,\ldots,x_p) \colon=\frac1{p!}\sum_{\s\in S_p} \sign(\s)\,A(\s\cdot(x_1,\ldots,x_p))~. $$ Then $\alt A$ is a $p$-Form on $E$ and $\alt\alt A=\alt A$. Denoting the subspace of all $p$-forms on $E$ by $\O^p(E)$ (and the subspace of all $q$-forms on $E^*$ by $\O_q(E)$) - i.e. $\O_q(E)=\O^q(E^*)$ - we see that $\alt:{\cal T}^p(E)\rar\O^p(E)$ is a projection onto.
$\alt(x^*\otimes y^*)=(x^*\otimes y^*-y^*\otimes x^*)/2$.
For all $A\in{\cal T}^p(E)$ and all $\pi\in S_p$ we have: $\alt(A\circ\pi)=\sign(\pi)\alt A$, where $A\circ\pi(x_1,\ldots,x_p)\colon=A(\pi\cdot(x_1,\ldots,x_p))$.
Suppose $\dim E=n$ and $x_1^*,\ldots,x_p^*\in E^*$. Then $$ \o(x_1,\ldots,x_p)\colon=\det(x_k^*(x_j))_{j,k=1}^p $$ is a $p$-form on $E$ - by $\det(a_{jk})$ we mean the determinant of the $n\times n$-matrix $(a_{jk})$.
Let $A,B,C$ be covariant tensors on $F$ and $u\in\Hom(E,F)$. Then the following assertions hold: 1. $u^*(\alt(A\otimes B))=\alt(u^*A\otimes u^*B)$ and 2. $\alt(A\otimes B)=\alt((\alt A)\otimes B)$.
$\proof$ 2. Suppose $A\in{\cal T}^p(E)$; since $\alt$ is linear we get by example: \begin{eqnarray*} p!\alt(\alt(A)\otimes B) &=&\sum_{\s\in S_p}\sign(\s)\alt(A\circ\s\otimes B)\\ &=&\sum_{\s\in S_p}\sign(\s)\alt((A\otimes B)\circ(\s\otimes id)) =\sum_{\s\in S_p}\alt(A\otimes B)~. \end{eqnarray*} $\eofproof$

Exterior product

Suppose $\o_1\in\O^p(E)$ and $\o_2\in\O^q(E)$ are two forms on $E$. The exterior product or wedge product is defined by \begin{equation}\label{alteq1}\tag{ALT1} \o_1\wedge\o_2\colon=\frac{(p+q)!}{p!q!}\alt(\o_1\otimes\o_2)~. \end{equation}
Take for example $x^*,y^*\in E^*$; these are $1$-forms on $E$ and their exterior product is a $2$-form given by $$ x^*\wedge y^* =2\alt(x^*\otimes y^*) =x^*\otimes y^*-y^*\otimes x^* $$ For a $2$-form $\o$ we get: \begin{eqnarray*} x^*\wedge\o(x,y,z) &=&3\alt(x^*\otimes\o)\\ &=&\Big(x^*(x)\o(y,z) -x^*(y)\o(x,z) -x^*(z)\o(y,x)\\ &&-x^*(x)\o(z,y) +x^*(y)\o(z,x) -x^*(z)\o(x,y)\Big)/2\\ &=&x^*(x)\o(y,z)-x^*(y)\o(x,z)+x^*(z)\o(x,y) \end{eqnarray*} More generally, for $x^*\in E^*$ and $\o\in\O^p(E)$ we have: \begin{equation}\label{alteq2}\tag{ALT2} x^*\wedge\o(x_0,\ldots,x_p)= \sum_{j=0}^p(-1)^jx^*(x_j)\o(x_0,\ldots,\wh{x_j},\ldots,x_p) \end{equation} where $\wh{x_j}$ means, that this component has to be omitted.
The exterior product is bi-linear, associative and for all $\o_1\in\O^p(F)$, $\o_2\in\O^q(F)$ and all $u\in\Hom(E,F)$ we have 1. $\o_1\wedge\o_2=(-1)^{pq}\o_2\wedge\o_1$ and 2. $u^*(\o_1\wedge\o_2)=u^*\o_1\wedge u^*\o_2$.
$\proof$ Suppose $\o_j\in\O^{p_j}(E)$, $j=1,\ldots,m$, then we infer by proposition: \begin{eqnarray*} (\o_1\wedge\o_2)\wedge\o_3 &=&\frac{(p_1+p_2+p_3)!}{(p_1+p_2)!p_3!} \alt((\o_1\wedge\o_2)\otimes\o_3)\\ &=&\frac{(p_1+p_2+p_3)!}{(p_1+p_2)!p_3!} \frac{(p_1+p_2)!}{p_1!p_2!} \alt(\alt(\o_1\otimes\o_2)\otimes\o_3)\\ &=&\frac{(p_1+p_2+p_3)!}{p_1!p_2!p_3!} \alt(\o_1\otimes\o_2\otimes\o_3) \end{eqnarray*} and by induction on $m$ we get: \begin{equation}\label{alteq3}\tag{ALT3} \bigwedge_{j=1}^m\o_j=\frac{(\sum p_j)!}{p_1!\ldots p_m!} \alt(\o_1\otimes\cdots\otimes\o_m)~. \end{equation} Now associativity follows readily. $\eofproof$
1. Suppose $\o\in\O^p(E)$. If $p$ is odd then: $\o\wedge\o=0$. 2. Let $e_1,\ldots e_{2n}$ be a basis for $E$ and put $$ \o\colon=\sum_{j=1}^ne_j^*\wedge e_{n+j}^*~. $$ Compute the $n$-fold exterior product of $\o$.
If all forms $\o_j$ are $1$-forms, i.e. $\o_j=x_j^*\in E^*$, then by \eqref{alteq3} implies \begin{eqnarray*} \bigwedge_{j=1}^m x_j^*(x_1,\ldots,x_m) &=&\sum_{\s\in S_m}\sign(\s)x_1^*\otimes\ldots\otimes x_m^* (x_{\s(1)},\ldots,x_{\s(m)})\\ &=&\sum_{\s\in S_m}\sign(\s)x_1^*(x_{\s(1)})\cdots x_m^*(x_{\s(m)}) =\det(x_k^*(x_j))_{j,k=1}^m~. \end{eqnarray*} Thus if $e_1,\ldots,e_n$ is a basis for $E$ with dual basis $e_1^*,\ldots,e_n^*$ and $p\leq n$, then for all $p$-tuples $J\colon=(j_1,\ldots,j_p)$, $j_1,\ldots,j_p\in\{1,\ldots,n\}$: $$ e_1^*\wedge\ldots\wedge e_p^*(e_{j_1},\ldots,e_{j_p})= \left\{\begin{array}{cl} \sign(j_1,\ldots,j_p)&\mbox{if $\{j_1,\ldots,j_p\}=\{1,\ldots,p\}$}\\ 0&\mbox{otherwise} \end{array}\right. $$ Moreover, putting $$ {\cal J}\colon=\{(j_1,\ldots,j_p):\,1\leq j_1 < \cdots < j_p\leq n=\dim E\} $$ and for any $J\in{\cal J}$: \begin{equation}\label{alteq4}\tag{ALT4} e_J^*\colon=\bigwedge_{j\in J}e_j^*, \end{equation} we conclude that the set $\{e_J^*:\,J\in{\cal J}\}$ forms a linearly independent subset of $\O^p(E)$. In fact, it's a basis, because for any $\o\in\O^p(E)$ we have: $$ \o=\sum_{J=\{j_1,\ldots,j_p\}\in{\cal J}}\o(e_{j_1},\ldots,e_{j_p})\,e_J^*~. $$ This can be verified as follows: take any $I=(i_1,\ldots,i_p)\in{\cal J}$, then $$ e_J^*(e_{i_1},\ldots,e_{i_p})=\left\{ \begin{array}{cl} 1&\mbox{if $J=I$}\\ 0&\mbox{otherwise} \end{array}\right. $$ In particular, if $\vol{}$ is a volume form on $E$ and $e_1,\ldots,e_n$ is a basis of $E$ such that $\vol{}(e_1,\ldots,e_n)=1$, i.e. $\vol{}$ is the volume form associated with the basis $e_1,\ldots,e_n$, then $$ \vol{}=e_1^*\wedge\ldots\wedge e_n^*~. $$
If $\dim E=n$, then $\dim\O^p(E)={n\choose p}$.

Universal property of alternating maps

For every $p$-linear alternating map $A:E^p\rar F$ there is exactly one linear map $\wt A:\O^p(E)\rar F$, such that for all $x_1,\ldots,x_p\in E$: $$ \wt A(x_1\wedge\ldots\wedge x_p)=A(x_1,\ldots,x_p)~. $$
$\proof$ Define $\wt A:{\cal T}^p(E)\rar F$ by $\wt A(x_1\otimes\cdots\otimes x_p)=A(x_1,\ldots,x_p)/p!$. Then by assumption: $$ \wt A(\alt(x_1\otimes\cdots\otimes x_p))=A(x_1,\ldots,x_p)/p! $$ and therefore: $\wt A(x_1\wedge\ldots\wedge x_p)=A(x_1,\ldots,x_p)$. $\eofproof$
For every linear functional $F:\O_p(E)\rar\R$ there is exactly one $A\in\O^p(E)$, such that for all $x_1,\ldots,x_p\in E$: $F(x_1\wedge\ldots\wedge x_p)=A(x_1,\ldots,x_p)$. Thus the dual of $\O_p(E)$ can be identified with $\O^p(E)$.

Contraction and exterior product

For all $x\in E$ and all $x_1^*,\ldots,x_p^*\in E^*$ we have: \begin{equation}\label{alteq5}\tag{ALT5} x\contract(x_1^*\wedge\ldots\wedge x_p^*) =\sum_{j=1}^p(-1)^{j-1}x_j^*(x)\, x_1^*\wedge\ldots\wedge\wh{x_j^*}\wedge\ldots\wedge x_p^* \end{equation} and more generally
Suppose $\o$ is a $p$-form and $\eta$ a $q$-form. Then for all $x\in E$: $$ x\contract(\o\wedge\eta) =(x\contract\o)\wedge\eta +(-1)^{p}\o\wedge(x\contract\eta)~. $$
$\proof$ Both sides are linear in $x$, $\o$ and $\eta$, thus it suffices to check both sides for $x=e_i$, $\o=\bigwedge_{j\in J}e_j^*$ and $\eta=\bigwedge_{k\in K}e_k^*$, which is pretty much straightforward. $\eofproof$
Let $x\in E$, $x^*\in E^*$ and $\o\in\O^p(E)$. Then: $x\contract(x^*\wedge\o)+x^\flat\wedge(x\contract\o)=x^*(x)\o$.
By proposition we have: $$ x\contract(x^*\wedge\o) =(x\contract x^*)\wedge\eta-x^*\wedge(x\contract\eta) =x^*(x)\eta-x^*\wedge(x\contract\eta)~. $$
Let $F\colon=[x^*=0]$ be a subspace of co-dimension $1$; choose $x\in E$ such that $x^*(x)=1$, then $\o\colon=x\contract\vol{}$ is a volume form on $F$ and $x^*\wedge\o=\vol{}$.
Since $x^*\wedge\vol{}=0$ we get by the previous example: $$ x^*\wedge(x\contract\vol{}) =x^*(x)\vol{}-x\contract(x^*\wedge\vol{}) =\vol{}~. $$
Suppose $\vol{}$ is a volume form on the $n$-dimensional space $E$. Then the mapping $J:x\mapsto x\contract\vol{}$ is an isomorphism from $E$ onto $\O^{n-1}(E)$.
Suppose $x\neq0$ then there are $e_2,\ldots,e_n\in E$, such that $x,e_2,\ldots,e_n$ forms a basis for $E$. Thus $x\contract\vol{}(e_2,\ldots,e_n)=\vol{}(x,e_2,\ldots,e_n)\neq0$, i.e. $x\contract\vol{}\neq0$: $J$ must be one-one. Since both $E$ and $\O^{n-1}(E)$ have the same dimension, $J$ must be an isomorphism.

Inner Products on Tensor Spaces

Extending inner products

 For all $A\in{\cal T}^p(E)$ the mapping $E^{*p}\rar\R$, $$ (x_1^*,\ldots,x_p^*)\mapsto A(x_1^{*\sharp},\ldots,x_p^{*\sharp}) $$ is $p$-linear, hence by the universal property of the tensor product there is a unique linear map $\la A,.\ra:{\cal T}^p(E)\rar\R$ such that $$ \la A,x_1^*\otimes\cdots,x_p^*\ra=A(x_1^{*\sharp},\ldots,x_p^{*\sharp})~. $$ It's easily checked that this is in fact a bi-linear form on ${\cal T}^p(E)\times{\cal T}^p(E)$ and it's symmetric, for \begin{equation}\label{ipteq1}\tag{IPT1} \la y_1^*\otimes\cdots\otimes y_p^*,x_1^*\otimes\cdots\otimes x_p^*\ra =\prod\la y_j^{*\sharp},x_j^{*\sharp}\ra~. \end{equation} In the case $p=1$ we get an inner product on the dual $E^*={\cal T}^1(E)$: $$ \la x^*,y^*\ra=y^*(x^{*\sharp})=\la x^{*\sharp},y^{*\sharp}\ra $$ which simply makes the musical isomorphism $\sharp:E\rar E^*$ an isometry, in particular both $E$ and $E^*$ have the same index.
Suppose $b_1,\ldots,b_n$ is an arbitrary basis for $(E,\la.,.\ra)$; put $g_{jk}\colon=\la b_j,b_k\ra$ - that's the Gramian of the basis. Let $b_1^*\ldots,b_n^*$ be the dual basis. Then the Gramian of $b_1^*\ldots,b_n^*$ is the inverse of the Gramian of $b_1\ldots,b_n$.
We infer from subsection and the symmetry of $g_{jk}$: $$ \la b_j^*,b_k^*\ra =\la b_j^{*\sharp},b_k^{*\sharp}\ra =\sum_{l,m} g^{lj}g_{lm}g^{mk} =g^{kj} =g^{jk}~. $$ Now suppose we are given an orthonormal basis $e_1,\ldots,e_n$ for $E$, then the Gramian of this basis coincides with its inverse: $$ \forall j,k:\quad\la e_j^*,e_k^*\ra=\la e_j,e_k\ra=\e_j\d_{jk}~. $$ Hence, by \eqref{ipteq1} the set $\{e_{j_1}^*\otimes\cdots\otimes e_{j_p}^*:\,j_1,\ldots,j_p\in\{1,\ldots,n\}\}$ is an orthonormal basis for ${\cal T}^p(E)$ - consequently $\la.,.\ra$ is not singular, i.e. it's an inner product on the space ${\cal T}^p(E)$ - and we have for all $A,B\in{\cal T}^p(E)$: $$ \la A,B\ra =\sum_{j_1,\ldots,j_p}\e_{j_1}\cdots\e_{j_p} A(e_{j_1},\cdots,e_{j_p})B(e_{j_1},\cdots,e_{j_p})~. $$ Analogously we can construct an inner product on ${\cal T}_p(E)$: $$ \forall A\in{\cal T}_p(E):\quad \la A,x_1\otimes\cdots\otimes x_p\ra=A(x_1^{\flat},\ldots,x_p^{\flat})~. $$ Identifying as usual the bi-dual $E^{**}={\cal T}_1(E)$ with $E$ we recover for $p=1$ the given inner product on $E$.
Every Euclidean product $\la.,.\ra$ on $E$ admits a $\C$-bi-linear extension on its complexification $\C\otimes E$: $$ (a\otimes x,b\otimes y)\mapsto ab\la x,y\ra~. $$ However, that's not a complex Euclidean product; the unique complex Euclidean product on $\C\otimes E$ extending the Euclidean product is given by $$ \la a\otimes x,b\otimes y\ra\colon=a\bar b\la x,y\ra~. $$
Suppose $E$ is an $n$-dimensional inner product space with index $\nu$. Prove that the index of ${\cal T}_p(E)$ is given by $$ \sum_{k=0}^{[(p-1)/2]}{p\choose 2k+1}\nu^{2k+1}(n-\nu)^{p-2k-1}~. $$
This is a combinatorial problem: suppose we are given i.i.d. random variables $X_1,\ldots,X_p$ such that $\P(X=-1)=\nu/n$ and $\P(X=1)=1-\nu/n$. We need to compute the probability $\P(X_1\cdots X_p=-1)$. An odd number of random variables must be negative and the remaing variables must be positive; thus we get $$ \P(X_1\cdots X_p=-1) =\sum_{k=0}{p\choose 2k+1}(\nu/n)^{2k+1}(1-\nu/n)^{p-2k-1}~. $$ Hence the index of ${\cal T}_p(E)$ is just this number multiplied by $n^p$.
Suppose $A_1,B_1\in{\cal T}^{p_1}(E)$ and $A_2,B_2\in{\cal T}^{p_2}(E)$. Prove that: $\la A_1\otimes A_2,B_1\otimes B_2\ra=\la A_1,B_1\ra\la A_2,B_2\ra$.
For any $G\in{\cal T}^2(E)$, the mapping $$ (x_1,\ldots,x_p),(y_1,\ldots,y_p)\mapsto\prod G(x_j,y_j) $$ has exactly one bi-linear extension $$ \wt G:{\cal T}^p(E)\times{\cal T}^p(E)\rar\R $$ such that $\wt G(x_1\otimes\cdots\otimes x_p,y_1\otimes\cdots\otimes y_p)=\prod G(x_j,y_j)$. If $G$ is symmetric, the so is $\wt G$.
Let $(E,\la.,.\ra)$ be an inner product space. Verify that the dual $u^{*d}\in\Hom(E^*)$ of the adjoint $u^*\in\Hom(E)$ of $u\in\Hom(E)$ is given by $$ u^{*d}(x^*)=(u(x^{*\sharp}))^\flat~. $$ Prove that this coincides with the adjoint $u^{d*}$ of the dual of $u$, i.e. $u^{*d}=u^{d*}$.
\begin{eqnarray*} \la x^*,u^{d*}y^*\ra &=&\la u^dx^*,y^*\ra =\la(u^dx^*)^\sharp,y^{*\sharp}\ra\\ &=&u^d(x^*)(y^{*\sharp}) =x^*(u(y^{*\sharp}))\\ &=&\la x^{*\sharp},u(y^{*\sharp})\ra =\la x^*,u(y^{*\sharp})^\flat\ra~. \end{eqnarray*}
If $u$ is an isometry, then so is $u^d\in\Hom(E^*)$.
By the previous exam we have $u^{*d}=u^{d*}$ and therefore $$ u^{d*}u^d =u^{*d}u^d =(uu^*)^d=1~. $$
Suppose $u\in\Hom(E)$ is an isometry of the inner product space $(E,\la.,.\ra)$. Prove that $A\mapsto u^*A$ is an isometry on ${\cal T}^p(E)$.
This simply follows from exam: \begin{eqnarray*} \la u^*(x_1^*\otimes\cdots\otimes x_p^*),u^*(y_1^*\otimes\cdots\otimes y_p^*)\ra &=&\la u^*(x_1^*)\otimes\cdots\otimes u^*(x_p^*),u^*(y_1^*)\otimes\cdots\otimes u^*(y_p^*)\ra\\ &=&\prod\la u^*(x_j^*),u^*(y_j^*)\ra =\prod\la x_j^*,y_j^*\ra =\la x_1^*\otimes\cdots\otimes x_p^*,y_1^*\otimes\cdots\otimes y_p^*\ra~. \end{eqnarray*}

Changing typ

On any inner product space $(E,\la.,.\ra)$ we can change the typ of a tensor quite obviously: suppose $A\in{\cal T}^p(E)$, then $$ \wh A(x_1^*,x_2,\ldots,x_p)\colon=A(x_1^{*\sharp},x_2,\ldots,x_p) $$ is a $(p-1,1)$ tensor. For example if $A=y_1\otimes\cdots\otimes y_p$, then $\wh A=y_1^\flat\otimes y_2\otimes\cdots\otimes y_p$. This way we can turn any $(p,q)$ tensor in an $(r,s)$ tensor provided the order is preserved, i.e. $s+r=p+q$.
Show that the stress tensor of a perfect fluid $T(X,Y)=\r\la X,V\ra\la Y,V\ra+\la X,Y\ra$ changed into a purely contravariant tensor $T^\sharp$ is given by $T^\sharp(A,B)=\r A(V)B(V)+PA(B^\sharp)$.
If $e_1,\ldots,e_n$ is an orthonormal basis and $T=\sum_{j,k}t_{jk}e_j\otimes e_k$, then its purely covariant form is $T^\flat=\sum_{j,k}\e_j\e_kt_{jk}e_j^*\otimes e_k^*$, where $\e_j=\la e_j,e_j\ra=\pm1$.

Inner products on $\O_p(E)$ and $\O^p(E)$

 The space $\O_p(E)$ is a subspace of ${\cal T}_p(E)$, the space of all contra-variant $p$-linear mappings $E^{*p}\rar\R$. First of all we want to determine the orthogonal projection from ${\cal T}_p(E)$ onto $\O_p(E)$. So take any permutation $\pi\in S_p$; we would like to compute the adjoint of the linear map $A\mapsto A\circ\pi$. For $A=x_1\otimes\cdots\otimes x_p$, $B=y_1\otimes\cdots\otimes y_p$ and $\s=\pi^{-1}$ we get: $$ \la A\circ\pi,B\ra =\prod_j\la x_{\pi(j)},y_j\ra =\prod_j\la x_{j},y_{\s(j)}\ra =\la A,B\circ\s\ra $$ i.e. the adjoint is given by $B\mapsto B\circ\pi^{-1}$. This in turn implies that $$ p!\,\alt^*(A)=\sum_{\pi\in S_p}A\circ\pi^{-1}=p!\,\alt(A) $$ i.e. $\alt^*=\alt$. Thus $\alt$ is self-adjoint and since $\alt\alt=\alt$, it's a self-adjoint projection, i.e. it's the orthogonal projection onto its image, which is $\O_p(E)$.
Suppose $x_1,\ldots,x_p,y_1,\ldots y_p\in E$,then $$ \la x_1\wedge\ldots\wedge x_p,y_1\wedge\ldots\wedge y_p\ra =p!\det(\la x_j,y_k\ra)~ . $$
$\proof$ Since $\alt$ is a self-adjoint projection, we conclude that: \begin{eqnarray*} \la x_1\wedge\ldots\wedge x_p,y_1\wedge\ldots\wedge y_p\ra &=&p!^2\la\alt(x_1\otimes\cdots\otimes x_p), \alt(y_1\otimes\cdots\otimes y_p)\ra\\ &=&p!^2\la\alt(x_1\otimes\cdots\otimes x_p), y_1\otimes\cdots\otimes y_p\ra\\ &=&p!\sum\sign(\pi)\prod_j\la x_{\pi(j)},y_j\ra =p!\det(\la x_j,y_k\ra) \end{eqnarray*} $\eofproof$

From now on we will always add the factor $1/p!$ to the inner product on $\O_p(E)$, but not on ${\cal T}_p(E)$.

This way the set $$ e_{j_1}\wedge\ldots\wedge e_{j_p},\quad 1\leq j_1 < j_2 < \cdots < j_p \leq n $$ becomes an orthonormal basis for $\O_p(E)$ and for all $x_1,\ldots,x_p,y_1,\ldots y_p\in E$ we have in $\O_p(E)$: \begin{equation}\label{ipteq2}\tag{IPT2} \la x_1\wedge\ldots\wedge x_p,y_1\wedge\ldots\wedge y_p\ra =\det(\la x_j,y_k\ra) \end{equation} So $\la x_1\wedge\ldots\wedge x_p,x_1\wedge\ldots\wedge x_p\ra$ is just the determinant of the Gramian of the vectors $x_1,\ldots,x_n$. In particular, if $x_1,\ldots,x_p$ is an orthonormal set of vectors in $E$ satisfying $\la x_j,x_j\ra=\e_j=\pm1$, then $$ \la x_1\wedge\ldots\wedge x_p,x_1\wedge\ldots\wedge x_p\ra =\det(\la x_j,x_k\ra) =\prod_j\la x_j,x_j\ra =\prod\e_j~. $$
Suppose $E$ is an $n$-dimensional inner product space with index $\nu$. Prove that the index of $\O_p(E)$ is given by $$ \sum_{j=0}^{[(p-1)/2]}{\nu\choose 2j+1}{n-\nu\choose p-2j-1}~. $$ In particular for $\nu=1$ the index of $\O_p(E)$ is ${n-1\choose p-1}$.
For $x\in E$ the adjoint of the map $A\mapsto x\otimes A$ in ${\cal T}_p(E)$ is given by $B\mapsto x^\flat\contract B$. Moreover, the adoint of $\o\mapsto x\wedge\o$ in $\O_p(E)$ is given by $\eta\mapsto x^\flat\contract\eta$.
$\proof$ 1. It suffices to verify that $$ \la x\otimes x_1\otimes\ldots\otimes x_p,y_1\otimes\ldots\otimes y_{p+1}\ra =\la x_1\otimes\ldots\otimes x_p, x^\flat\contract y_1\otimes\ldots\otimes y_{p+1}\ra $$ By definition the left hand side is $\la x,y_1\ra\la x_1,y_2\ra\ldots\la x_p,y_{p+1}\ra$ and the right hand side equals $x^\flat(y_1)\la x_1,y_2\ra\ldots\la x_p,y_{p+1}\ra$.
2. Since $\alt^*=\alt$ and $\alt(\eta)=\eta$ we infer from \eqref{alteq3} and 1. that for all $\o\in\O_p(E)$ \begin{eqnarray*} \frac1{(p+1)!}\la x\wedge\o,\eta\ra &=&\frac1{p!}\la\alt(x\otimes\o),\eta\ra =\frac1{p!}\la x\otimes\o,\alt(\eta)\ra\\ &=&\frac1{p!}\la x\otimes\o,\eta\ra =\frac1{p!}\la \o,x^\flat\contract\eta\ra~. \end{eqnarray*} where $\la.,.\ra$ denotes the inner product on ${\cal T}_p(E)$, i.e. for the inner product on $\O_{p+1}(E)$ and $\O_{p}(E)$ we have: $$ \forall x\in E\, \forall\o\in\O_p(E)\, \forall\eta\in\O_{p+1}(E):\quad \la x\wedge\o,\eta\ra =\la\o,x^\flat\contract\eta\ra~. $$ $\eofproof$

The Hodge $*$-operator

Definition

Suppose $n=\dim E$, $e_1,\ldots,e_n$ is an orthonormal basis for $E$ with dual basis $e_1^*,\ldots,e_n^*$ and volume form $\vol{}=e_1^*\wedge\ldots\wedge e_n^*$ associated with the ONB $e_1,\ldots,e_n$. Since $\dim\O^n(E)=1$, every $n$-form is a multiple of $\vol{}$. Hence for all $\o\in\O^p(E)$ and all $\eta\in\O^{n-p}(E)$: $$ \o\wedge\eta=\colon F(\eta)\vol{} $$ for some functional $F:\O^{n-p}(E)\rar\R$; in fact it's a linear functional. As $\O^{n-p}(E)$ is an inner product space (cf. subsection there is a unique $*\o\in\O^{n-p}(E)$ such that \begin{equation}\label{hsoeq3}\tag{HSO3} \forall \eta\in\O^{n-p}(E)\qquad \o\wedge\eta=\la*\o,\eta\ra\vol{}~. \end{equation} It's easily verified that the operator $*:\O^{p}(E)\rar\O^{n-p}(E)$ is lineare; it's called the Hodge $*$-operator. It's the algebraic equivalent of the geometric association: $F\mapsto F^\perp$, which assignes to each $p$-dimensional subspace $F$ its orthogonal complement $F^\perp$. Evidently, the Hodge $*$-operator depends on the volume form, but since this form is associated with an ONB there are only two possibilities: $F$ or $-F$.
If $u\in\Hom(E)$ is an orientation preserving isometry on the inner product space $(E,\la.,.\ra)$, the for all $\o\in\O^p(E)$: $*(u^*\o)=u^*(*\o)$.
Since $u$ is an orientation preserving isometry we have $u^*\vol{}=\vol{}$. Hence by proposition: $$ u^*\o\wedge u^*\eta =u^*(\o\wedge\eta) =\la*\o,\eta\ra u^*\vol{} =\la*\o,\eta\ra\vol{}~. $$ By exam: $\la*\o,\eta\ra=\la u^*(*\o),u^*\eta\ra$ and thus by definition \eqref{hsoeq3}: $*(u^*\o)=u^*(*\o)$.
Prove that for all $\o,\eta\in\O^p(E)$: $\o\wedge*\eta=\eta\wedge*\o$.
By definition: $\o\wedge*\eta=\la*\o,*\eta\ra\vol{}$ and $\eta\wedge*\o=\la*\eta,*\o\ra\vol{}$.

The Hodge $*$-operator on an orthonormal basis

We now determine how $*$ operates on a particular orthonormal basis of $\O^p(E)$: So let $e_1,\ldots,e_n$ be an ONB for $E$ with dual basis $e_1^*,\ldots,e_n^*$. Put $q+p=n$, ${\cal J}=\{(j_1,\ldots,j_p):1\leq j_1 < \cdots < j_p\leq n\}$ and ${\cal I}=\{(i_1,\ldots,i_q):1\leq i_1 < \cdots < i_q\leq n\}$. For $J\in{\cal J}$ and - cf. \eqref{alteq4}: $$ e_J^*\colon=\bigwedge_{j\in J}^p e_j^*, $$ we compute $*e_J^*$ for $\vol{}\colon=e_1^*\wedge\ldots\wedge e_n^*$: Put $e_I^*\colon=e_{i_1}^*\wedge\ldots\wedge e_{i_q}^*$ for some $I\in{\cal I}$; if $I\cap J\neq\emptyset$ then $e_J^*\wedge e_I^*=0$, i.e.: $\la*e_J^*,e_I^*\ra=0$. It follows by \eqref{hsoeq3} that $*e_J^*$ is a multiple of $e_{J^c}^*$, i.e. $*e_J^*=c_pe_{J^c}^*$. By definition: $e_J^*\wedge e_{J^c}^*=\sign(J,J^c)\vol{}$ and $\la*e_J^*,e_{J^c}^*\ra=c_p\la e_{J^c}^*,e_{J^c}^*\ra$, thus: $c_p=\la e_{J^c}^*,e_{J^c}^*\ra\sign(J,J^c)=\pm1$. It remains to compute $\la e_{J^c}^*,e_{J^c}^*\ra$: let $\nu$ denote the index of $(E,\la.,.\ra)$, then we have: $$ \la e_{J^c}^*,e_{J^c}^*\ra\la e_J^*,e_J^*\ra =\prod_{j=1}^n\la e_j^*,e_j^*\ra =\prod_{j=1}^n\la e_j,e_j\ra =(-1)^\nu~. $$ Moreover, $\sign(J,J^c)\sign(J^c,J)=(-1)^{pq}$ and therefore: \begin{equation}\label{hsoeq4}\tag{HSO4} *e_J^*=(-1)^\nu\la e_J,e_J\ra\sign(J,J^c)e_{J^c}^* \quad\mbox{and}\quad **\o=(-1)^{\nu+pq}\o \end{equation} Finally we have $$ \la*\o_1,*\o_2\ra\vol{} =\o_1\wedge*\o_2 =(-1)^{pq}*\o_2\wedge\o_1 =(-1)^{pq}\la**\o_2,\o_1\ra\vol{} =(-1)^{\nu}\la\o_2,\o_1\ra\vol{}~. $$ which implies that $*:\O^p(E)\rar\O^{n-p}(E)$ is an isometry for even index $\nu$ and an anti-isometry for $\nu$ odd. Moreover the adjoint map of $\o\mapsto*\o$ is given by: $\o\mapsto(-1)^{pq}*\o$, for $$ \la*\o_1,\o_2\ra\vol{} =\o_1\wedge\o_2 =(-1)^{pq}\o_2\wedge\o_1 =(-1)^{pq}\la*\o_2,\o_1\ra\vol{}~. $$ Eventually, instead of \eqref{hsoeq3} we could have taken equally well: \begin{equation}\label{hsoeq5}\tag{HSO5} \forall\o,\eta\in\O^p(E)\qquad \o\wedge*\eta=(-1)^\nu\la\o,\eta\ra\vol{}~. \end{equation} On $\O_p(E)$ the map $*$ is defined similarly: $$ \forall \o,\eta\in\O_{p}(E)\qquad \o\wedge*\eta=(-1)^\nu\la\o,\eta\ra\vol{}~. $$ This obviously implies that \begin{equation}\label{hsoeq6}\tag{HSO6} *e_J=(-1)^\nu\la e_J,e_J\ra\sign(J,J^c)e_{J^c},\quad *^*=(-1)^{pq}* \quad\mbox{and}\quad **=(-1)^{\nu+pq}~. \end{equation}
Let $E$ be an inner product space with index $\nu$, then $*\vol{}=1$ and $*1=(-1)^\nu\vol{}$.
For $n$ even the only possible eigenvalues of the operator $*:\O^{n/2}(E)\rar\O^{n/2}(E)$ are $\pm1,\pm i$.
Let $E$ be a $2$-dimensional Euclidean space. Then $*:\O_1(E)\rar\O_1(E)$ is a rotation by $\pi/2$.
Take a positive orthonormal basis $e_1,e_2$. Since $*e_1=e_2$ und $*e_2=-e_1$, the conclusion follows.
If $E$ is Euclidean and $e_1,\ldots,e_n$ an orthonormal basis, then $*e_J=\sign(J,J^c)e_{J^c}$, and $*^*=(-1)^{pq}*$ and $**=(-1)^{pq}$.
If $E$ is Lorentz, then $*^*=(-1)^{pq}*$ and $**=(-1)^{pq+1}$.
If $\dim E$ is odd, then $*^*=*$ and $**=(-1)^\nu$.
Let $E$ be a $3$-dimensional Euclidean space. Determine the isometries $*:\O_1(E)\rar\O_2(E)$ and $*:\O_2(E)\rar\O_1(E)$.
Take a positive orthonormal basis $e_1,e_2,e_3$ and put $V=e_1\wedge e_2\wedge e_3$. By \eqref{hsoeq4} we have for $\o=e_J$ by exam: $*e_J=\sign(J,J^c)e_{J^c}$, i.e.: $$ *e_1=e_2\wedge e_3,\quad *e_2=e_3\wedge e_1,\quad *e_3=e_1\wedge e_2 $$ and as $**=1$: $$ *(e_1\wedge e_2)=e_3\quad *(e_2\wedge e_3)=e_1,\quad *(e_3\wedge e_1)=e_2~. $$
Suppose $E$ is an $n$-dimensional Euclidean space with orthonormal basis $e_1,\ldots,e_n$ and dual basis $e_1^*,\ldots,e_n^*$. Putting $\eta_j\colon=e_1^*\wedge\ldots\wedge\wh{e_j^*}\wedge\ldots\wedge e_n^*$, we have: $$ *e_j^* =(-1)^{j-1}\eta_j=e_j\contract\vol{} \quad\mbox{and more generally}\quad \forall x^*\in E^*\quad *x^*=x^{*\sharp}\contract\vol{} $$ where $\vol{}=e_1^*\wedge\ldots\wedge e_n^*$ is the volume form on $E$. For the contra-variant version we get: $$ \forall x\in E\quad *x=x^{\flat}\contract\vol{} $$
Let $E$ be an inner product space and $x_1,\ldots,x_n$ a basis for $E$, then $*(x_1\wedge\ldots\wedge x_p)$ is orthogonal to all $x_I$ where $I\colon=\{(i_1,\ldots,i_q):\exists j:i_j\in\{1,\ldots,p\}\}$ and $q\colon=n-p$. Show that $$ *\bigwedge_{j=1}^p x_j =\la\bigwedge_{j=p+1}^n e_j,\bigwedge_{j=p+1}^n e_j\ra\det(e_j^*(x_k))_{j,k=1}^p\bigwedge_{j=p+1}^n e_j $$ where $e_1,\ldots,e_p$ is an ONB of $F\colon=\lhull{x_1,\ldots,x_p}$ and $e_{p+1},\ldots,e_n$ an ONB of $F^\perp$ - we assume $F$ is not degenerated.
Put $$ \o\colon=\bigwedge_{j=1}^p x_j \quad\mbox{and}\quad \eta\colon=\bigwedge_{j=p+1}^n e_j $$ Then $$ \det(e_j^*(x_k))_{j,k=1}^p\vol{} =\det(e_j^*(x_k))_{j,k=1}^p\bigwedge_{j=1}^p e_j\wedge\eta =\o\wedge\eta =\la*\o,\eta\ra\vol{} =c\la\eta,\eta\ra\vol{} $$ As $\la\eta,\eta\ra=\pm1$ it follows that $c=\la\eta,\eta\ra\det(e_j^*(x_k))_{j,k=1}^p$.
Let $E$ be an $n$-dimensional inner product space and put $$ x_1\times\cdots\times x_{n-1}\colon=*(x_1\wedge\ldots\wedge x_{n-1})~. $$ Then this vector is always orthogonal to the $n-1$ vectors $x_1,\ldots,x_{n-1}$ and we have: $$ \la x_1\times\cdots\times x_{n-1}, x\ra =\vol{}(x_1,\ldots,x_{n-1},x)~. $$
Let $E$ be a $3$-dimensional Euclidean space. Then $*(x\wedge y)$ coincides with the vector product $x\times y$ and we have: $$ \la x\times y,z\ra=\vol{}(x,y,z)\quad\mbox{und}\quad \norm{x\times y}^2=\Vert x\Vert^2\norm y^2-\la x,y\ra^2~. $$
As $*(e_1\wedge e_2)=e_3$, $*(e_2\wedge e_3)=e_1$, $*(e_3\wedge e_1)=e_2$, we conclude that: $$ *(x\wedge y) =(x_1y_2-x_2y_1)e_3+(x_2y_3-x_3y_2)e_1+(x_3y_1-x_1y_3)e_2 =x\times y~. $$ 2. By definition: $$ \la x\times y,z\ra V(e_1^*,e_2^*,e_3^*) =\la*(x\wedge y),z\ra V(e_1^*,e_2^*,e_3^*) =x\wedge y\wedge z(e_1^*,e_2^*,e_3^*) $$ and by \eqref{alteq1} this equals $e_1^*\wedge e_2^*\wedge e_3^*(x,y,z)=\vol{}(x,y,z)$.
3. $\la x\times y,x\times y\ra=\la *(x\wedge y),*(x\times y)\ra=\la x\wedge y,x\wedge y\ra$ and by lemma this equals $$ \det\left(\begin{array}{cc} \la x,x\ra&\la x,y\ra\\ \la y,x\ra&\la y,y\ra \end{array}\right) =\Vert x\Vert^2\norm y^2-\la x,y\ra^2 $$
Let $\o\in\O_p(E)$. Verify that: $*(x\wedge\o)=(-1)^p x^\flat\contract*\o$ and conclude that in case $E$ is a $3$-dimensional Euclidean space: $x\times(y\times z)=y\la x,z\ra-z\la y,x\ra$.
By definition we have for any $\eta\in\O_{n-p-1}(E)$: \begin{eqnarray*} \la*(x\wedge\o),\eta\ra\vol{} &=&(x\wedge\o)\wedge\eta =(-1)^p\o\wedge x\wedge\eta\\ &=&(-1)^p\la*\o,x\wedge\eta\ra\vol{} =(-1)^p\la x^\flat\contract*\o,\eta\ra\vol{} \end{eqnarray*} 2. In case $E$ is a $3$-dimensional Euclidean space we get for $\o=*(y\wedge z)$ by proposition: \begin{eqnarray*} x\times(y\times z) &=&*(x\wedge*(y\wedge z)) =-x^\flat\contract**\o =-x^\flat\contract(y\wedge z)\\ &=&-(x^\flat\contract y)z+(x^\flat\contract z)y =y\la x,z\ra-z\la y,x\ra \end{eqnarray*}
Suppose $(E,\la.,.\ra)$ is Euclidean. For $u\in\Hom(E)$ compute the matrix $(c_{jk})$ of the linear mapping $$ u^*:\O^{n-1}(E)\rar\O^{n-1}(E),\quad u^*(\o)(x_1,\ldots,x_{n-1})=\o(u(x_1),\ldots,u(x_{n-1})) $$ with respect to the orthonormal basis $*e_1^*,\ldots,*e_n^*$ of $\O^{n-1}(E)$.
By lemma or \eqref{hsoeq2} we get $$ c_{jk}=\la *e_j,u^*(*e_k)\ra =(-1)^{j+k}\la\eta_j,u^*\eta_k\ra =(-1)^{j+k}\det(\la e_l^*,u^*(e_m^*)\ra)_{l\neq j,m\neq k} $$ Let $A=(a_{jk})$ be the matrix of $u$ with respect to the orthonormal basis $e_1,\ldots,e_n$; as $\la e_l,u^*(e_m^*)^\sharp\ra=a_{ml}$, we infer that $c_{jk}$ is the determinant of the $(n-1)\times(n-1)$ sub-matrix obtained by deleting the $k$-th row and $j$-th column of $A$ and then multiplying by $(-1)^{j+k}$. This matrix $(c_{jk})$ is known as the adjugate matrix $\adj A$ of the matrix $A=(a_{jk})$: $$ (\adj A)_{jk}\colon=(-1)^{j+k}\det(a_{ml})_{m\neq k,l\neq j}~. $$
Prove that for any matrix $A\in\Ma(n,\R)$ we have: $A\cdot\adj A=\det A$.
Suppose the matrix of $u\in\Hom(E)$ with respect to the orthonormal basis $e_1,\ldots,e_n$ is $A$; since $\o\wedge*\eta=\la\o,\eta\ra\vol{}$ we get by the definition of the adjugate matrix: \begin{eqnarray*} \det A\,\vol{} &=&\det u\,\vol{} =\det u^*\,e_1^*\wedge\ldots\wedge e_n^*\\ &=&u^*(e_1^*)\wedge\ldots\wedge u^*(e_n^*) =(-1)^{j-1}u^*(e_j^*)\wedge u^*\eta_j\\ &=&u^*(e_j^*)\wedge u^*(*e_j^*) =\sum_m a_{jm}e_m^*\wedge\sum_l(\adj A)_{lj}(*e_l^*)\\ &=&\sum_{l,m} a_{jm}(\adj A)_{lj}e_m^*\wedge(*e_l^*) =\sum_l a_{jl}(\adj A)_{lj}\vol{} \end{eqnarray*} Analogously we get for $j\neq k$: $\sum_l a_{jl}(\adj A)_{lk}=0$.

The Hodge $*$-operator in relativistic electrodynamics

Let $E$ be a $4$-dimensional Lorentz space. Compute the operators $*:\O_2(E)\rar\O_2(E)$, $*:\O_1(E)\rar\O_3(E)$ and $*:\O_3(E)\rar\O_1(E)$.
1. $*e_0\wedge e_1=e_2\wedge e_3$, $*e_0\wedge e_2=-e_1\wedge e_3$, $*e_0\wedge e_3=e_1\wedge e_2$, $*e_1\wedge e_2=-e_0\wedge e_3$, $*e_1\wedge e_3=e_0\wedge e_2$, $*e_2\wedge e_3=-e_0\wedge e_1$. Thus the matrix of $*:\O_2(E)\rar\O_2(E)$ with respect to the basis: $e_0\wedge e_1,e_0\wedge e_2,e_0\wedge e_3,e_1\wedge e_2,e_1\wedge e_3,e_2\wedge e_3$ is $$ \left(\begin{array}{cccccc} 0&0&0&0&0&-1\\ 0&0&0&0&1&0\\ 0&0&0&-1&0&0\\ 0&0&1&0&0&0\\ 0&-1&0&0&0&0\\ 1&0&0&0&0&0 \end{array}\right) $$ 2. By \eqref{hsoeq6} we get: $*e_0=--+e_1\wedge e_2\wedge e_3$, $*e_1=-+-e_0\wedge e_2\wedge e_3$, $*e_2=-++e_0\wedge e_1\wedge e_3$ and $*e_3=-+-e_0\wedge e_1\wedge e_2$ and as $**=1$ on $\O_1(E)$: $*e_0\wedge e_1\wedge e_2=e_3$, $*e_0\wedge e_1\wedge e_3=-e_2$, $*e_0\wedge e_2\wedge e_3=e_1$, $*e_1\wedge e_2\wedge e_3=e_0$.
In relativity electromagnetic fields are described by an alternating $(2,0)$-tensor field $\O$ (called electromagnetic field tensor) on a Lorentz manifold $M$. For any instantaneous observer $Z$ the electric field $E$ for $Z$ is given by $-(Z\contract\O)^\sharp$ and the magnetic field $B$ is given by $-(Z\contract*\O)^\sharp$. 1. Prove that $E$ and $B$ are in the rest space of $Z$. 2. Compute both fields for $\O=E^{0*}\wedge E^{3*}$ and $Z=\cosh(\vp)E^0+\sinh(\vp)E^2$ in Minkowski space, i.e. $M=\R_1^4$. 3. The symmetric tensor field $$ T(Z,W)\colon=\la Z\contract\O,W\contract\O\ra-\frac12\la\O,\O\ra\la Z,W\ra $$ is called the stress-energy tensor field. Compute $T(Z,Z)$. If $X,Y$ are unit fields in the rest space $Z^\perp$ of $Z$, then $T(X,Y)$ is the force exerted on a unit surface in $Z^\perp$ normal to $X$ in the direction of $Y$ (cf. section).
1. By definition of musical isomorphisms, contractions and alternating forms we have $$ \la(Z\contract\O)^\sharp,Z\ra =Z\contract\O(Z) =\O(Z,Z)=0~. $$ and therefore $(Z\contract\O)^\sharp$ is in the rest space of $Z$.
2. In this case we get by proposition: $$ -E^\flat= Z\contract\O =Z\contract(E^{0*}\wedge E^{3*}) =E^{0*}(Z)E^{3*}-E^{3*}(Z)E^{0*} =\cosh(\vp)E^{3*}, $$ i.e. $E=-\cosh(\vp)E^3$. Analogously we infer from $*\O=E^{1*}\wedge E^{2*}$: $-B^\flat=-\sinh(\vp)E^{1*}$, i.e. $B=\sinh(\vp)E^1$. Hence an observer moving in the direction of $E^2$ with velocity $\tanh(\vp)$ (with respect to $E^0$) experiences an electric field $E=-\cosh(\vp)E^3$ in the direction of $-E^3$ and a magnetic field $B=\sinh(\vp)E^1$ in the direction of $E^1$.
3. Finally $\la\O,\O\ra=-1$ and $\la Z,Z\ra=-1$. Hence $$ T(Z,Z)=\cosh^2(\vp)-\frac12 =\frac12(\cosh^2(\vp)+\sinh^2(\vp)) =\frac12(\norm E^2+\norm B^2)~. $$
Given an observer field $Z$ on a four dimensional Lorentz manifold $M$. 1. Suppose we know the electric field $E\colon=-(Z\contract\O)^\sharp$ and the magnetic field $B\colon=-(Z\contract*\O)^\sharp$. Show that we can recover $\O$ from this knowledge. 2. Prove that \begin{eqnarray*} \la\O,\O\ra&=&-\la*\O,*\O\ra=-\norm E^2+\norm B^2 \quad\mbox{and}\\ T(Z,Z)&=&\frac12(\norm E^2+\norm B^2)~. \end{eqnarray*} Classically the latter is known as the energy density of the electromagnetic field. 3. Verify that $$ \la\O,*\O\ra=-2\la E,B\ra~. $$ Though the vectors $E_m$ and $B_m$ at a point $m\in M$ depend on the instantaneous observer $Z_m$, the values $-\norm{E_m}^2+\norm{B_m}^2$ and $2\la E_m,B_m\ra$ do not depend on $Z_m$! On the other hand the energy density at $m$ depends on $Z_m$.
Let $Z=E^0,E^1,E^2,E^3$ be an ONB, then put $a_{jk}=-\O(E^j,E^k)$ and $E^{jk*}\colon=E^{j*}\wedge E^{k*}$, then $E^{jk*}$, $0\leq j < k\leq3$, is an ONB and we put $$ -\O=a_{01}E^{01*}+a_{02}E^{02*}+a_{03}E^{03*}+a_{12}E^{12*}+a_{13}E^{13*}+a_{23}E^{23*}~. $$ This implies that $a_{0j}=\la E,E^j\ra=-\O(Z,E^j)=-\O(E^0,E^j)$, i.e. $$ E =\sum_{j=1}^3\la E,E^j\ra E^j =a_{01}E^1+a_{02}E^2+a_{03}E^3~. $$ By exam it follows that $$ -*\O=a_{01}E^{23*}-a_{02}E^{13*}+a_{03}E^{12*}-a_{12}E^{03*}+a_{13}E^{02*}-a_{23}E^{01*} $$ and therefore $\la B,E^j\ra=-*\O(Z,E^j)=-*\O(E^0,E^j)$ $$ B =\sum_{j=1}^3\la B,E^j\ra E^j =-a_{23}E^1+a_{13}E^2-a_{12}E^3~. $$ Thus we know $a_{0j}=-\O(Z,E^j)$ and also $-a_{12}=-*\O(Z,E^3)$, $a_{13}=-*\O(Z,E^2)$ and $-a_{23}=-*\O(Z,E^1)$, i.e. $$ -\O=\O(Z,E^j)E^{01*}+\O(Z,E^2)E^{02*}+\O(Z,E^3)E^{03*} +*\O(Z,E^3)E^{12*}-*\O(Z,E^2)E^{13*}+*\O(Z,E^1)E^{23*} $$ It follows that $$ \la\O,\O\ra =-\O(Z,E^1)^2-\O(Z,E^2)^2-\O(Z,E^3)^2+*\O(Z,E^3)^2+*\O(Z,E^2)^2+*\O(Z,E^1)^2 =-\la E,E\ra+\la B,B\ra~. $$ Thus $$ T(Z,Z) =\frac12(\la E,E\ra+\la B,B\ra)\geq0 $$ i.e. $T$ is positive on instantaneous observers!
3. We get $$ \la\O,*\O\ra =2(a_{01}a_{23}-a_{02}a_{13}+a_{03}a_{12}) =-2\la E,B\ra~. $$ Finally, the energy density in the previous exam is $\cosh^2(\vp)-1/2$; thus it depends on $\vp$ and therefore on the instantaneous observer.
If $E_j=-\O(Z,E^j)$ and $B_j=-*\O(Z,E^j)$ are the components of $E$ and $B$, respectively, with respect to the ONB $E^1,E^2,E^3$ of $Z^\perp$, then \begin{eqnarray*} -\O &=&E_1E^{01*}+E_2E^{02*}+E_3E^{03*}-B_3E^{12*}+B_2E^{13*}-B_1E^{23*}\\ -*\O &=&E_1E^{23*}-E_2E^{13*}+E_3E^{12*}+B_3E^{03*}+B_2E^{02*}+B_3E^{01*} \end{eqnarray*}
Prove that the linear map $X_m\mapsto(X_m\contract\O_m)^\sharp$ is skew symmetric, i.e. for all $X_m,Y_m\in T_mM$: $\la(X_m\contract\O_m)^\sharp,Y_m\ra=-\la X_m,(Y_m\contract\O_m)^\sharp\ra$. 2. If $Z_m\in T_mM$ is an instantaneous observer minimizing $X_m\mapsto\norm{X_m\contract\O_m)^\sharp}^2$, then $Z_m$ is an eigen-vector of $$ X\mapsto((X\contract\O)^\sharp\contract\O)^\sharp~. $$
The matrices of $Z\mapsto-Z\contract\O$ and $Z\mapsto-Z\contract*\O$ are given by: $$ \left(\begin{array}{cccc} 0&a_{01}&a_{02}&a_{03}\\ a_{01}&0&-a_{12}&-a_{13}\\ a_{02}&a_{12}&0&-a_{23}\\ a_{03}&a_{13}&a_{23}&0 \end{array}\right) \quad\mbox{and}\quad \left(\begin{array}{cccc} 0&-a_{23}&a_{13}&-a_{12}\\ -a_{23}&0&a_{03}&-a_{02}\\ a_{13}&-a_{03}&0&-a_{01}\\ -a_{12}&a_{02}&a_{01}&0 \end{array}\right) $$
Compute $E$ and $B$ for $\O=E^{0*}\wedge E^{1*}+E^{0*}\wedge E^{3*}+E^{2*}\wedge E^{3*}$ and $Z=\cosh(\vp)E^0+\sinh(\vp)E^2$ in Minkowski space, i.e. $M=\R_1^4$. Show that neither the electric nor the magnetic field vanishes for any instantaneous observer.
The matrices of $Z\mapsto-Z\contract\O$ and $Z\mapsto-Z\contract*\O$ are given by: $$ \left(\begin{array}{cccc} 0&1&0&1\\ 1&0&0&0\\ 0&0&0&-1\\ 1&0&1&0 \end{array}\right) \quad\mbox{and}\quad \left(\begin{array}{cccc} 0&-1&0&0\\ -1&0&1&0\\ 0&-1&0&-1\\ 0&0&1&0 \end{array}\right)~. $$ As both linear mappings are non singular, neither the electric nor the magnetic field vanishes for any instantaneous observer. In particular we get $-Z\contract\O=\cosh(\vp)(E^1+E^3)+\sinh(\vp)E^3$ and $-Z\contract*\O=-\cosh(\vp)E^1+\sinh(\vp)(E^1+E^3)$, i.e. the fields are both normal to $E^0$ and $E^2$.
← Lorentz Spaces → Glossary
<Home>
Last modified: Mon Dec 2 16:00:03 CET 2024