Subgroups of $\Gl(n,\bK)$
In this section we are going to discuss some matrix subgroups, which are in general not finite but carry an additional structure: real differentiability. First let us fix some notation. By $\Ma(n,\bK)$ we denote the algebra of $n\times n$-matrices with entries in a field $\bK$ - in this chapter we will deal exclusively with the cases $\bK=\R$ or $\bK=\C$. The set
$$
\Gl(n,\bK)\colon=\{A\in\Ma(n,\bK):\det A\neq0\}
$$
with matrix multiplication is the so called linear group over the field $\bK$. In particular we notice the special linear, the orthogonal and the special orthogonal group:
\begin{eqnarray*}
\Sl(n,\bK)&\colon=&\{A\in\Gl(n,\bK):\det A=1\},\\
\OO(n)&\colon=&\{A\in\Gl(n,\R):A^tA=1\},\\
\SO(n)&\colon=&\OO(n)\cap\Sl(n,\R)~.
\end{eqnarray*}
The last two groups are subgroups of $\Gl(n,\R)$. Replacing the real with the complex numbers we similarly get the unitary and the special unitary group:
\begin{eqnarray*}
\UU(n)&\colon=&\{A\in\Gl(n,\C):\bar A^tA=1\},\\
\SU(n)&\colon=&\{A\in\UU(n):\det A=1\},
\end{eqnarray*}
where as usual $A^t$ denotes the transpose and $\bar A$ the complex conjugate of the matrix $A$. Also, the $n$-dimensional torus $\TT^n$ is isomorphic to a commutative subgroup of $\UU(n)$: it's the set of all diagonal matrices $diag\{z_1,\ldots,z_n\}$, $z_1,\ldots,z_n\in S^1$. All these groups admit the standard representation: every $g=(g_{jk})\in G\sbe\Gl(n,\bK)$ operates on $\bK^n$ by mapping $(x_1,\ldots,x_n)\in\bK^n$ to the vector $(y_1,\ldots,y_n)\in\bK^n$, where
$$
y_j=\sum_{k=1}^n g_{jk}x_k
\quad\mbox{or more concisely}\quad
y=g\cdot x,
$$
where $x$ and $y$ are interpreted as $n\times1$ matrices, i.e. column-vectors and $\cdot$ is matrix multiplication. We know that every representation of a finite group can be decomposed into irreducibles and we will see that this also holds for compact groups; however, it's no longer true for arbitrary groups, even for the additive group $(\R,+)$ this doesn't hold! Take e.g. the following representation $A:\R\rar\Gl(2,\R)$ of the additive group $\R$:
$$
A(a)\colon=\left(\begin{array}{cc}
1&a\\
0&1
\end{array}\right),\quad\mbox{then}\quad
A(a)A(b)=A(a+b),
$$
so it's indeed a representation. Obviously $\R e_1$ is an invariant subspace of this representation, but for every vector $x\colon=ue_1+ve_2$, $v\neq0$, the vectors $A(a)x=(u+av)e_1+ve_2$, $a\in\R$, generate the whole space $\R^2$. So $\R^2$ cannot be decomposed into irreducible sub-spaces.
Tangent spaces
All of the matrix groups we'll be considering are real sub-manifolds of some space $\R^{n+k}$. Thus we need a handy definition of a sub-manifold: A subset $M$ of $\R^{n+k}$ is called an $n$-dimensional sub-manifold of $\R^{n+k}$ if for every point $x\in M$ there is a smooth function $F:U\rar\R^k$ defined on an open neighborhood $U$ of $x$ in $\R^{n+k}$ such that $M\cap U=[F=0]$ and $DF(x)$ is onto. Most if not all of our sub-manifolds will actually be of the form $[F=0]$, i.e. there will only be one function $F$. The kernel $\ker DF(x)$ is called the tangent space of $M$ at $x$, denoted by $T_xM$, it's evidently a real vector-space. $T_xM$ coincides with the set of derivatives of smooth curves, i.e.
$$
T_xM=\{c^\prime(0):c:(-\d,\d)\rar M\mbox{ is smooth and }c(0)=x\}~.
$$
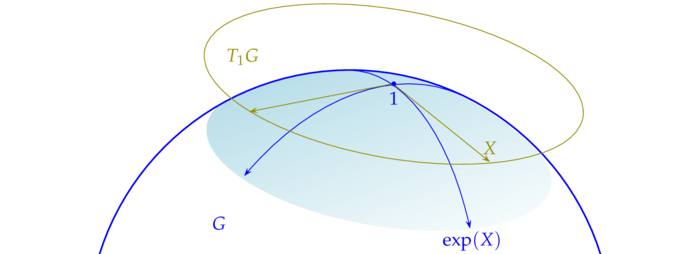
The right hand side is a subspace of the left hand side by the chain rule, but as for the converse we need some form of the implicit function theorem, which implies that there is some smooth function $H$ in a neighborhood $V$ of $0$ in $\R^n$ such that $H(0)=x$ and $\im DH(0)=\ker DF(x)$ - actually $[F=0]$ is locally the graph of $H$. Now let $G$ be any closed subgroup of $\Gl(n,\bK)$ - we simply call it a matrix Lie-group. It's indeed a sub-manifold of $\Gl(n,\bK)$ (this is not at all obvious!) and thus we may put:
$$
\GG\colon=T_1G\colon=\{c^\prime(0):c:(-\d,\d)\rar G, c(0)=1\}~.
$$
This is the tangent space of $G$ at the identity $1$ i.e. unit matrix and it's generally called the Lie-algebra of $G$. $\GG$ is a real vector-space, i.e. if $t\in\R$, $X,Y\in\GG$, then $tX,X+Y\in\GG$. Moreover, we'll shortly see that it's furnished with an additional algebraic structure.
Being Lie-algebras not merely vector-spaces these spaces carry an additional algebraic structure: it's not matrix multiplication, it's the Lie-bracket $[A,B]\colon=AB-BA$, cf. lemma. Generally, an algebra will be a vector-space $A$ with an additional binary operation $(x,y)\mapsto xy$, which is assumed to be bi-linear; in our case this operation is the Lie-bracket. So be careful, the Lie-algebra $\Ma(n,\bK)$ is not the same as the algebra $\Ma(n,\bK)$ with matrix multiplication!
Let $E^{jk}$ denote the standard basis of $\Ma(n,\C)$, i.e. there is only one non vanishing entry: the $j$-th row and $k$-th column is $1$. For $\uu(n)$ we may take: $E^{11},\ldots,E^{nn}$, and if $j < k$: $E^{jk}-E^{kj}$ and $iE^{jk}+iE^{kj}$. For $\su(n)$ we take instead of the first $n$ basis vectors the vectors $E^{11}-E^{22},\ldots,E^{n-1,n-1}-E^{nn}$.
Left invariant vector fields
As in the case of a sub-manifold we need a working definition of vector fields on sub-manifolds of $\R^{n+k}$: Given a sub-manifold $M$ of $\R^{n+k}$ a vector field $X$ on $M$ is a smooth mapping $m\mapsto X_m$ defined in a neighborhood of $M$ with values in $\R^{n+k}$, such that for all $m\in M$: $X_m\in T_mM$. The flow of $X$ is a smooth map $\theta:{\cal D}\rar M$ defined on an open subset ${\cal D}$ of $\R\times M$ such that
By the well known Picard-Lindelöf Theorem from ODE the flow exists and is uniquely determined by $X$. If ${\cal D}=\R\times M$, then the vector field $X$ is said to be complete. Here we are only concerned with the special case where $M$ is a matrix Lie-group $G$. So we set out to discuss the simplest case - the group $\Gl(n,\R)$, which is an open subset of $\Ma(n,\R)=\R^{n^2}$. For any $X\in\Ma(n,\R)$ we define a vector field $X_A\colon=AX$ on $\Gl(n,\R)$, i.e. a smooth mapping $A\mapsto X_A$ from $\Gl(n,\R)$ into $\Ma(n,\R)$. $X_A$ is uniquely defined by the following condition: if $L_A$ denotes left translation, i.e.: $L_A(B)=AB$, then $X_A=DL_A(1)X=AX$ - this is called left invariance of the vector field. Similarly $R_A(B)\colon=BA$ is right translation! The flow $\theta(t,A)$ of the vector field $X_A$ is defined by $\theta(0,A)=A$ and $\pa_t\theta(t,A)=X_{\theta(t,A)}$, i.e.. $\theta_t(A)\colon=\theta(t,A)$ is the solution to the initial value problem
$$
\ttd t\theta_t(A)=X_{\theta_t(A)}\colon=\theta_t(A)X,\quad
\theta_0(A)=A~.
$$
This is a linear ODE whose solution can be calculated easily: $\theta(t,A)=A\exp(tX)$, for
$$
\ttd tA\exp(tX)
=A\exp(tX)X
=DL_{A\exp(tX)}(X)
=X_{A\exp(tX)}~.
$$
In particular: left invariant vector fields are complete. The general case of an arbitrary matrix Lie-group $G$ with Lie-algebra $\GG$ turns out to be almost obvious: Since for $X\in\GG$ the restriction of the left invariant vector field $A\mapsto X_A=DL_A(1)X=AX$ to $G$ is a vector field on $G$, i.e. $X_A\in T_AG\colon=L_A(T_1G)$, we have:
$$
X\in\GG\quad\Rar\quad\exp(tX)\in G,
$$
$\exp:\GG\rar G$ is called the exponential map of the Lie-algebra $\GG$ of $G$ into $G$, cf. e.g. wikipedia. Thus for all matrix Lie-groups $G$ the exponential map $\exp:\GG\rar G$ is just the restriction of the exponential map $\exp:\Ma(n)\rar\Gl(n)$.