Subgroups of $\OO(3)$
Cf. students version in German
Symmetries of a molecule
The symmetries of a molecule are, of course, the symmetries of a geometric model of a molecule. As for this model, we assume that it comprises point-like atoms at fixed positions in euclidean space. A symmetry is just a linear isometry (also called orthogonal transformation) $g:\R^3\rar\R^3$, which maps the model onto itself in such a way, that the original model and its image are indistinguishable. The set of all these operations form a subgroup of the orthogonal group $\OO(3)$, it is called the group of symmetries of the molecule, cf. wikipedia. We say that two symmetries $g_1$ and $g_2$ are of the same type if they are conjugate in $\OO(3)$, i.e. $g_2=ug_1u^{-1}$ for some $u\in\OO(3)$. Equivalently: $g_1$ and $g_2$ are of the same type if there exist orthonormal bases such that the matrix of $g_1$ with respect to the first basis and the matrix of $g_2$ with respect to the second basis coincide. The concept of conjugacy (cf. subsection), which is widely used in group theory, is more restrictive than the notion of similarity of matrices. The type of an orthogonal transformation $g\in\OO(3)$ can essentially be characterized by two numbers: $\det g$ and $\tr g$: By the spectral theorem of linear algebra we can find for every orthogonal operator $g\in\OO(3)$ a positively oriented orthonormal basis $b_1,b_2,b_3$, a sign $\e\in\{\pm1\}$ and a unique real number $\theta\in(-\pi,\pi]$, such that:
$$
g(b_1)=\e b_1,\quad
g(b_2)=\cos(\theta)\,b_2+\sin(\theta)b_3,\quad
g(b_3)=-\sin(\theta)\,b_2+\cos(\theta)b_3~.
$$
In other words: the matrix of $g$ with respect to the basis $b_1,b_2,b_3$ has the following form
\begin{equation}\label{dsr3eq1}\tag{SGO1}
\left(\begin{array}{ccc}
\e&0&0\\
0&\cos\theta&-\sin\theta\\
0&\sin\theta&\cos\theta
\end{array}\right),
\end{equation}
thus $\det g=\e$ and $\tr g=\e+2\cos\theta$. If $\det g=1$ then $g$ is said to be a proper rotation and the subgroup $\SO(3)\colon=\{g\in\OO(3):\det g=1\}$ is called the special orthogonal group; the number $\theta\in(-\pi,\pi]$ is essentially determined by $\cos\theta=(\tr g-1)/2$ and is called the angle of rotation. Since $g(b_1)=b_1$, $b_1$ or $\R b_1$ is said to be the axis of rotation. If $\e=\det g=-1$ then $g$ is called an improper rotation, $b_1$ or $\R b_1$ the (improper) axis of rotation, because $g(b_1)=-b_1$, and $\theta$, which satisfies $\cos\theta=(\tr g+1)/2$, the (improper) angle of rotation. Of course symmetries of the same type have the same trace and the same determinant, but a little bit more is true:
In general our notation does not distinguish between a linear operator $A\in\Hom(E)$ of an $n$ dimensional vector-space $E$ over the field $\bK$ from the matrix $A\in\Ma(n,\bK)$ of this operator with respect to a fixed basis: usually the context dictates what is meant! In the sequel we will stick to notions common in chemistry for symmetries. Usually a group of symmetries is a finite subgroup of the orthogonal group; there are only a few exceptions: for homo-nuclear diatomic molecules like $\chem{O_2}$ or linear molecules like $\chem{CO_2}$ the groups of symmetry are infinite! Suppose the group of symmetries is finite, then each symmetry of the molecule is a composition of a finite set of elementary types of symmetries, which can be described as follows:
- The identity $E$ (or $1$): $\det E=1$, $\tr E=3$; the inversion $I$: $\det I=-1$, $\tr I=-3$.
- The reflection $\s$ about some plane: $\det\s=-1$, $\tr\s=1$; in particular the reflections $\s(xy),\s(yz),\s(zx)$ about the coordinate planes.
- Let $n\geq2$ be a natural number. $C_n$ and $S_n$ respectively will denote a proper and an improper rotation, respectively, by the angle $2\pi/n$. The axis of rotation is said to be an $C_n$-axis and an $S_n$-axis, respectively.
Of course, $E$, $I$ and $\s$ are special cases of rotations or improper rotations. A molecule may have different $C_n$- or $S_n$-axes, anyway, in chemistry the axis with the largest value of $n$ is called the main axis.
Remember the following definitions from group theory: 1. A mapping $F:G\rar H$ of a group $G$ into a group $H$ is called a homomorphism if for all $x,y\in G$: $F(xy)=F(x)F(y)$. If in addition $F$ is a bijection, then $F$ is said to be an isomorphism. 2. If $G,H$ are groups then $G\times H$ with the binary operation $(g_1,h_1)(g_2,h_2)\colon=(g_1g_2,h_1h_2)$ is a group. 3. A subset $H$ of a group $(G,\cdot)$ is called a subgroup (of $G$) if for all $x,y\in H$: $x\cdot y^{-1}\in H$; this is the case if and only if $(H,\cdot)$ is a group. 4. If $A$ is a subset of a group $G$ then the "smallest" subgroup $H$ of $G$ containing $A$ is called the group generated by $A$, i.e. $H$ is the intersection of all subgroups of $G$ containing the set $A$. The elements of $A$ are called generators of $H$.
In sage this can be done as follows:
G=direct_product_permgroups([CyclicPermutationGroup(2),CyclicPermutationGroup(2)])
labels=['(0,0)','(1,0)','(0,1)','(1,1)']
CG=G.cayley_table(names=labels)
print(CG)
This will give you the Cayley table of $\Z_2^2$, elements labeled $(0,0),(1,0),(0,1),(1,1)$:
$$
\begin{array}{c|cccc}
\Z_2^2&(0,0)&(1,0)&(0,1)&(1,1)\\
\hline
(0,0)&(0,0)&(1,0)&(0,1)&(1,1)\\
(1,0)&(1,0)&(0,0)&(1,1)&(0,1)\\
(0,1)&(0,1)&(1,1)&(0,0)&(1,0)\\
(1,1)&(1,1)&(0,1)&(1,0)&(0,0)
\end{array}
$$
Put $G=\{e,a,b,c\}$ and define a group structure on $G$ by the following Cayley table
$$
\begin{array}{c|cccc}
G&e&a&b&c\\
\hline
e&e&a&b&c\\
a&a&e&c&b\\
b&b&c&e&a\\
c&c&b&a&e
\end{array}
$$
Then $F(e)\colon=(0,0)$, $F(a)\colon=(1,0)$, $F(b)\colon=(0,1)$, $F(c)\colon=(1,1)$ defines an isomorphism $F:G\rar\Z_2^2$.
Matrices of symmetries
Given a matrix of a rotation we can easily figure out its axis and its angle of rotation. But sometimes we have to go the other way round; we need to find a matrix representation $U$ of a rotation with given axis $b$, $\norm b=1$, and angle of rotation $t$, with respect to a given positive orthonormal basis $e_1,e_2,e_3$. How to accomplish this? First we compute the matrices $A$ and $P$ (with respect to $e_1,e_2,e_3$) of the linear map $x\mapsto b\times x$ and the orthogonal projection $x\mapsto x-\la x,b\ra b$ onto $b^\perp$ respectively.
We claim that $U$ is given by:
$$
U=\exp(tA)=1+(\cos(t)-1)P+\sin(t)A~.
$$
Indeed, we have $Ub=b$ and for a unit vector $x\perp b$: $Ux=\cos(t)x+\sin(t)b\times x$; now $b\times x$ is in the plane $b^\perp$, it's orthogonal to $x$ and its norm is $1$; thus $b,x,b\times x$ is a positive orthonormal basis and it's mapped to $b$, $\cos(t)x+\sin(t)b\times x$ and $\cos(t)b\times x-\sin(t)x$. Hence $U|b^\perp$ is a rotation in $b^\perp$ by $t$. Alternatively one may verify: $U^*U=1$, $\det U=+1$ and $\tr U=1+2\cos t$, which implies that $U$ is a proper rotation by $t$ or $-t$.
$Ae_1=b\times e_1=(-e_2-2e_3)/\sqrt6$, $Ae_2=(e_1+e_3)/\sqrt6$, $Ae_3=(2e_1-e_2)/\sqrt6$ and thus the matrix of $A$ with respect to the basis $e_1,e_2,e_3$:
$$
A=\frac1{\sqrt6}\left(\begin{array}{ccc}
0&1&2\\
-1&0&-1\\
-2&1&0
\end{array}\right)
\quad\mbox{and}\quad
P=-A^2=\frac1{6}\left(\begin{array}{ccc}
5&-2&1\\
-2&2&2\\
1&2&5
\end{array}\right)
$$
For the improper rotation about the axis $b$, $\norm b=1$, by the angle $t$ we get:
$$
V\colon=-1+(\cos(t)+1)P+\sin(t)A~.
$$
Of course this can be verified along the same lines. However, this time we establish the identity $V^*V=1$ by brute force calculation: notice that $A^*=-A$, $P^*=P$, $A^2=-P$ and $AP=PA$:
\begin{eqnarray*}
V^*V
&=&(-1+(1+\cos t)P-\sin t\,A)(-1+(1+\cos t)P+\sin t\,A)\\
&=&1+(1+\cos t)^2P+\sin^2tP
-(1+\cos t)P-\sin t\,A\\
&&-(1+\cos t)P+\sin t(1+\cos t)PA
+\sin t\,A-\sin t(1+\cos t)AP\\
&=&1+(1+2\cos t+\cos^2t+\sin^2t-2-2\cos t)P=1~.
\end{eqnarray*}
As for the determinant choose some normalized vector $e\in b^\perp$, then $b,e,b\times e$ is a positive orthonormal basis and it's mapped by $V$ to $-b,b\times e,-e$, which is a negative orthonormal basis. It follows that $\det V=-1$.
A particular case $(t=0)$ of an improper rotation is a reflection $\s$ about the plane orthogonal to $b$:
$$
\s(x)=-x+2Px=-x+2(x-\la x,b\ra b)=x-2\la x,b\ra b~.
$$
The group $C_{nv}$
This group is generated by a $C_n$-rotation and a reflection $\s_1$ about a plan vertical to the plane of rotation such that: $\s_1C_n=C_n^{-1}\s_1$ - the latter implies: $\s_1C_n^k=C_n^{-k}\s_1$. In math it's called the dihedral group: the group of symmetries of the regular $n$-gon and thus it's in fact a subgroup of $\OO(2)$, cf. wikipedia. $C_{nv}$ contains exactly $2n$ symmetries: the rotations $C_n^0=E,\ldots,C_n^{n-1}$ and the reflections $\s_l=\s_1C_n^{l-1}$, $l=1,\ldots,n$.
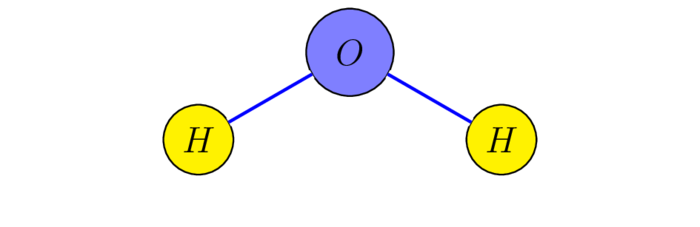
Only $C_{2v}$ is commutative, it's the symmetry group of water $\chem{H_2O}$ and its Cayley table is given by:
$$
\begin{array}{c|cccc}
C_{2v}&E&C_2&\s_1&\s_2\\
\hline
E &E &C_2 &\s_1&\s_2\\
C_2 &C_2 &E &\s_2&\s_1\\
\s_1&\s_1&\s_2&E &C_2\\
\s_2&\s_2&\s_1&C_2 &E
\end{array}
$$
where $\s_1(x,y,z)=(x,-y,z)$, $\s_2(x,y,z)=(-x,y,z)$, $C_2(x,y,z)=(-x,-y,z)$ and the water molecule being placed in the $yz$-plane! The mapping $E\mapsto(0,0)$, $C_2\mapsto(1,1)$, $\s_1\mapsto(0,1)$, $\s_2\mapsto(1,0)$ is easily checked to establish an isomorphism $C_{2v}\rar\Z_2^2$.
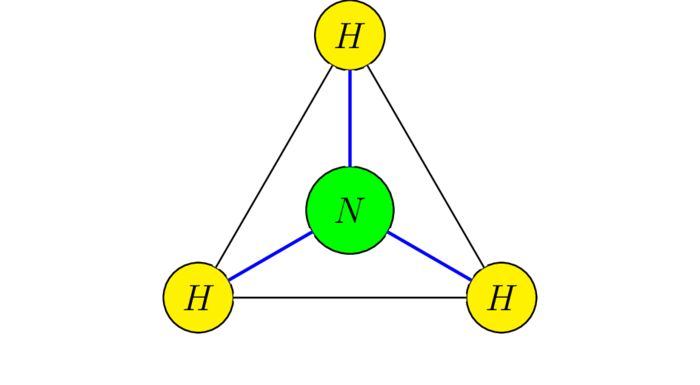
$C_{3v}$ is the group of symmetries of ammonia $\chem{NH_3}$ - we assume that the hydrogen atoms form an equilateral triangle in the $xy$-plane and the nitrogen atom is located right over the center of the triangle. Denoting the rotations by $E$, $C_3$, $C_3^*=C_3^{-1}$ and the reflections by $\s_1,\s_2$ and $\s_3$, the following sage code
D=DihedralGroup(3)
CD=D.cayley_table()
head=CD.row_keys()
print(head)
labels=['E','\s_1','\s_3','C_3','C_3^*','\s_2']
CD=D.cayley_table(names=labels)
latex(CD)
will give you the Cayley table of $C_{3v}$:
$$
\begin{array}{c|cccccc}
C_{3v}&E&\s_1&\s_3&C_3&C_3^*&\s_2\\
\hline
E&E&\s_1&\s_3&C_3&C_3^*&\s_2\\
\s_1&\s_1&E&C_3&\s_3&\s_2&C_3^*\\
\s_3&\s_3&C_3^*&E&\s_2&\s_1&C_3\\
C_3&C_3&\s_2&\s_1&C_3^*&E&\s_3\\
C_3^*&C_3^*&\s_3&\s_2&E&C_3&\s_1\\
\s_2&\s_2&C_3&C_3^*&\s_1&\s_3&E\\
\end{array}
$$
It's isomorphic to $S(3)$: indeed every symmetry $g\in C_{3v}$ permutes the hydrogen atoms and this association establishes an isomorphism!
The group $C_{nh}$
This commutative group is generated by a $C_n$ rotation a reflection $\s$ about the plane of rotation. The group comprises $2n$ isometries: $\s^jC_n^k$, $k=0,\ldots,n-1$, $j=0,1$. $C_{2h}$ is again isomorphic to $\Z_2^2$.
$C_n$: the cyclic group of order $n$
This group needs just one $C_n$ generator; it's commutative and isomorphic to $\Z_n$, i.e. $\{0,\ldots,n-1\}$ with addition modulo $n$.
$T_d$: the group of symmetries of the tetrahedron
Let $e_1,e_2,e_3$ be an orthonormal basis of $\R^3$. The vectors $a_1=e_1+e_2+e_3$, $a_2=-e_1+e_2-e_3$, $a_3=e_1-e_2-e_3$ and $a_4=-e_1-e_2+e_3$ constitute the vertices of a regular tetrahedron $T$ in $\R^3$.
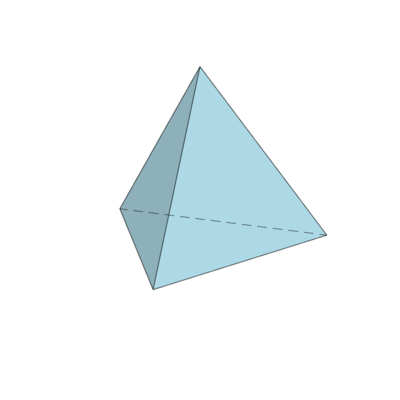
Which type of symmetries represent the following matrices and how do they act on the vertices?
$$
\left(\begin{array}{ccc}
1&0&0\\
0&1&0\\
0&0&1
\end{array}\right),
\left(\begin{array}{ccc}
0&1&0\\
0&0&1\\
1&0&0
\end{array}\right),
\left(\begin{array}{ccc}
1&0&0\\
0&-1&0\\
0&0&-1
\end{array}\right),
\left(\begin{array}{ccc}
-1&0&0\\
0&0&1\\
0&-1&0
\end{array}\right),
\left(\begin{array}{ccc}
0&0&-1\\
0&1&0\\
-1&0&0
\end{array}\right)
$$
-
This is the identity $E$, it acts on the vertices just like the permutation $(1234)$.
-
The determinant is $+1$, hence it's a rotation and for the angle $\theta\in(-\pi,\pi]$ we get: $1+2\cos\theta=0$, i.e. $\theta=\pm2\pi/3$, and the axis: $\R a_1$. Thus its type of symmetry is $C_3$ and it acts on the vertices like the permutation $(1342)$, which is the cycle $(2,3,4)$.
-
The determinant is $+1$ and the trace is $-1$; thus it's a rotation by $\pi$; it's type of symmetry is $C_2$. The axis of rotation: $\R e_1$ and it acts on the vertices like the permutation $(3412)$.
-
The determinant is $-1$ and the trace is $-2$; thus it's an improper rotation by $\pm\pi/2$; its type of symmetry is $S_4$. The axis of rotation is $\R e_1$ and it acts on the vertices like the permutation $(2341)$, which is the cycle $(1,2,3,4)$.
-
The determinant is $-1$ and the trace is $1$; thus it's a reflection; it's type of symmetry is $\s$. The normal to the reflection plane is $(e_1+e_3)/\sqrt2$ and it acts on the vertices like the permutation $(2134)$.
The group generated by these symmetries is the group of symmetries of the tetrahedron, it's actually isomorphic to $S(4)$. The list above is of course not a minimal list of generators!
The orthogonal projection $P$ is an isometry (in the euclidean sense) from the positive face $K\colon=\convex{e_1,\ldots.e_{n+1}}=B_1^{n+1}\cap(H+N/\sqrt{n+1})$ of the convex set $B_1^{n+1}\colon=\{x\in\R^{n+1}:\sum|x_j|\leq1\}$ onto $C\colon=\convex{a_1,\ldots,a_{n+1}}$, for $Px=x-\la x,N\ra N$ simply moves the hyperplane $H+N/\sqrt{n+1}=[\la.,N\ra=1/\sqrt{n+1}]$ to the subspace $H=[\la.,N\ra=0]$. Thus for all $j\neq k$: $\norm{a_j-a_k}=\norm{e_j-e_k}=\sqrt 2$.
$O_h$: the group of symmetries of the cube and the octahedron
Octahedron is just another name for the set $B_1^3$. Suppose $\pi\in S(3)$ is a permutation and $\e_1,\e_2,\e_3\in\{\pm1\}$. The group of symmetries of the cube consists of all linear isometries $g\in\OO(3)$, given by $g:e_k\mapsto\e_k e_{\pi(k)}$. The order of this group is thus $2^3\cdot 3!=48$.
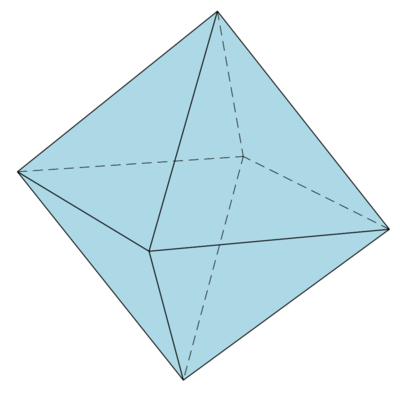
Obviously the trace and the determinant of the symmetry $g$ are given by: $\tr g=\sum\e_k\d_{k\pi(k)}$ and $\det g=\e_1\e_2\e_3\sign(\pi)$. A permutation $\pi\in S(3)$ can only have one or three fix-points or none; in the first case the trace may have the values: $\pm1$; in the second case its possible values are $\pm1,\pm3$ and in the latter case it can only have the value $0$. Thus $\tr g=\pm1+2\cos(2\pi/n)\in\{-3,-1,0,1,3\}$ or $2\cos(2\pi/n)\in\{-2,-1,0,1,2\}$, implying: $2\pi/n\in\{\pi,2\pi/3,\pi/2,\pi/3\}$ or $n\in\{2,3,4,6\}$.
Again, this is not a minimal list of generators!
- The determinant is $-\e$ and the trace is $\e$. For $\e=-1$ it's a proper rotation by $\pi$ about the third axis: $C_2$. For $\e=1$ it's an improper rotation by $0$ about the first axis, i.e. a reflection about the $yz$-plane: $\s_1$.
- The determinant is $-\e$ and the trace is $1$. For $\e=-1$ it's a proper rotation by $\pi/2$ about the first axis: $C_4$. For $\e=1$ it's an improper rotation by $0$ about $\R(0,1,1)$, i.e. a reflection about the plane perpendicular to $(0,1,1)$: $\s_2$.
- The determinant is $\e$ and the trace is $-1$. For $\e=-1$ it's an improper rotation by $\pi/2$ about the first axis: $S_4$. For $\e=1$ it's a proper rotation by $\pi$ about $\R(0,1,1)$: $C_2$.
- The determinant is $\e$ and the trace is $0$. For $\e=-1$ it's an improper rotation by $\pi/3$ about $\R(1,-1,1)$: $S_6$. For $\e=1$ it's a proper rotation by $2\pi/3$ about $\R(1,1,1)$: $C_3$.
- The determinant is $-\e$ and the trace is $0$. For $\e=-1$ it's a proper rotation by $2\pi/3$ about $\R(-1,1,1)$: $C_3$. For $\e=1$ it's an improper rotation by $\pi/3$ about $\R(1,1,-1)$: $S_6$.
We remark that the reflections $\s_1$ and $\s_2$ are of course conjugate in $\OO(3)$ and hence they are of the same type, however they are not conjugate in $O_h$, i.e. there is no $g\in O_h$ such that $\s_2=g\s_1g^{-1}$!
Computer algebra programs usually generate groups as subgroups of some $S(n)$, cf Cayley's Theorem or exam. In e.g.sage the full group $O_h$ can be generated as a subgroup of $S(6)$:
Oh=PermutationGroup([(2,3,4,1),(6,4,5,2),(6,3,5,1),(3,1)])
To determine the representatives of the conjugacy classes of $O_h$ and the size of their classes use the series of commands:
Reps=Oh.conjugacy_classes_representatives()
for g in Reps:
cg=Oh.conjugacy_class(g)
print(g.domain(),len(cg))
The last command should give you a list of representatives and the size of their conjugacy class; in our case there are 10 conjugacy classes and they contain $1,3,3,6,6,6,6,8,8,1$ elements.
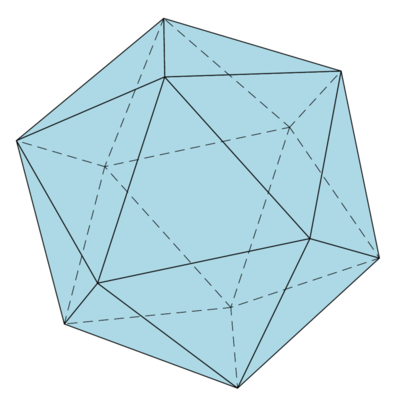
$I_h$: the group of symmetries of the icosahedron
The symmetry group of the icosahedron ($12$ vertices, $30$ edges and $20$ faces) and its dual the dodecahedron consists of $60$ proper rotations: 1. Choose any pair of antipodal vertices and rotate by multiples of $2\pi/5$ - this gives $6\cdot4=24$ rotations. 2. Choose any pair of centers of opposite faces and rotate by $2\pi/3$ and $4\pi/3$ - this gives $10\cdot2=20$ rotations. 3. Choose any pair of midpoints of opposite edges and rotate by $\pi$ - this gives $15\cdot1=15$ rotations. Adding the identity we therefore get $60$ rotations. The group of proper rotations is isomorphic to $A(5)$, the subgroup of $S(5)$ which is made up of all even permutations (cf. e.g. construction and properties of the icosahedron). There are another $60$ improper rotations and the whole group of symmetries of the icosahedron is isomorphic to $A(5)\times\Z_2$.
Put $a=(1+\sqrt5)/2$ (the golden ratio), then the vertices obtained by cyclical permutation of the coordinates of the four vertices $(\pm a,\pm1,0)$ form the vertex set of an icosahedron. Cf. e.g. coordinates. A typical face is given by the vertices: $(a,1,0),(0,a,1),(1,0,a)$
The following sage commands will do it (the last command will generate a $\LaTeX$ code of the Cayley table).
G=AlternatingGroup(4)
n=G.order()
labels=[str(i+1) for i in range(n)]
GT=G.cayley_table(names=labels)
head=GT.row_keys()
for i in range(n):
string=labels[i]+':= '
string+=str(head[i].domain())
print(string)
latex(GT)
Molecular Vibrations
Cf. students version in German
Some additional groups
We already mentioned the orthogonal group $\OO(n)$ of all linear isometries (also called orthogonal transformations) of the euclidean space $\R^n$; it can be identified with a subgroup of the group $\Gl(n,\R)$ - the set of all invertible $n\times n$-matrices, more precisely $\OO(n)=\{U\in\Gl(n): U^*U=1\}$. The special orthogonal group $\SO(n)$ is the subgroup of $\OO(n)$ comprising all matrices $U\in\OO(n)$ satisfying $\det U=+1$. The complex analogue of $\OO(n)$ is the unitary group $\UU(n)$, it's the set of all linear isometries (also called unitary transformations) of the complex euclidean space $\C^n$ and can in turn be identified with the set of matrices $U\in\Gl(n,\C)$ such that $U^*U=1$. Remember: if $A=(a_{jk})$ is in $\Ma(n,\C)$, then $A^*$ is given by $(\bar a_{kj})$, i.e. $A^*$ is the complex conjugate of the transposed of $A$!
$\SU(n)\colon=\{U\in\UU(n):\det U=+1\}$ is called the special unitary group. $\UU(1)$ is the unit circle $S^1\colon=\{z\in\C:|z|=1\}$ (the group operation is multiplication) which is isomorphic to the torus $\TT\colon=\R/2\pi\Z$, i.e. addition in $\R$ $\modul\ 2\pi$. The space of functions $f:\TT\rar\C$ may thus be identified with the space of $2\pi$-periodic functions $f:\R\rar\C$: if $f:\R\rar\C$ is $2\pi$-periodic then there is exactly one function $F:S^1\rar\C$ such that for all $x\in\R$: $F(e^{ix})=f(x)$. $F$ is continuous, smooth, etc. if and only if $f$ is continuous, smooth, etc.
Let $e_1,\ldots,e_n$ be the standard ONB of $\C^n$ and $b_1,\ldots,b_n$ any ONB of $E$. Define an isomorphism $J:\C^n\rar E$ by $Je_j=b_j$, then $U\mapsto JUJ^{-1}$ is an isomorphism of $\UU(n)$ onto $\UU(E)$.
The site representation of a molecule
The symmetry group of a molecule simply permutes atoms of the same type. This gives rise to what is called the site representation of the molecule in some space $\C^n$. It is a particular case of a unitary representation, i.e. a homomorphism $\Psi:G\rar\UU(n)$ into the group of unitary matrices. Of course, if the group of symmetries is generated by $g_1,\ldots,g_n$, then it suffices to determine $\Psi(g_1),\ldots,\Psi(g_n)$. In case $\Psi$ is injective the representation is called faithful. The site representation of a molecule need not be faithful: the reflection $\s_2$ in the symmetry group of $\chem{H_2O}$ (cf. subsection) leaves all three atoms invariant, i.e. $\Psi(\s_2)=1$. If $\Psi$ is a faithful representation, then the subgroup $\Psi(G)$ of $\UU(n)$ is isomorphic to $G$.
For example, any $g\in T_d$ permutes the hydrogen atoms of methane $\chem{CH_4}$ and leaves the carbon atom invariant, cf. the group $T_d$. Thus we obtain the following representation $\Psi$ of $T_d$ in $\C^4$ - we disregard the central carbon atom:
$$
\Psi(C_3)=\left(\begin{array}{cccc}
1&0&0&0\\
0&0&0&1\\
0&1&0&0\\
0&0&1&0
\end{array}\right),
\Psi(C_2)=\left(\begin{array}{cccc}
0&0&1&0\\
0&0&0&1\\
1&0&0&0\\
0&1&0&0
\end{array}\right),
\Psi(S_4)=\left(\begin{array}{cccc}
0&0&0&1\\
1&0&0&0\\
0&1&0&0\\
0&0&1&0
\end{array}\right),
\Psi(\s)=\left(\begin{array}{cccc}
0&1&0&0\\
1&0&0&0\\
0&0&1&0\\
0&0&0&1
\end{array}\right),
$$
In math groups are somehow the abstract mathematical structures that can describe transformations without referring to any objects out there and a representation of a group is the action of the group on a particular set of objects. In the previous example the object is a model of the methane molecule.
The standard representation, $\det$ and the trivial representation
Since any symmetry group $G$ is a subgroup of $\OO(3)$, the canonical inclusion map $G\rar\OO(3)\rar\UU(3)$ is a unitary representation, it's called the standard representation - it's clearly faithful. Also $g\mapsto\det(g)$ is a representation and it's only 'in-equivalent' to the trivial representation $g\mapsto1$ if $G$ contains both proper and improper rotations - both are in general not faithful.
The standard representation of $S(n)$
Assigning each permutation $\pi$ the matrix $P(\pi)=(p_{jk})$, where $p_{\pi(k)k}=1$ and otherwise $p_{jk}=0$, i.e. $P(\pi)e_k=e_{\pi(k)}$, we get a unitary representation $P$ of $S(n)$ in $\C^n$ (or an orthogonal representation of $S(n)$ in $\R^n$). Indeed for all $k$: $P(\s)P(\pi)e_k=P(\s)e_{\pi(k)}=e_{\s(\pi(k))}=e_{\s\pi(k)}=P(\s\pi)e_k$.
Vibrations
Let us assume $n$-atoms comprise a molecule and the potential energy of the molecule attains a (local) minimum when the atoms are located at positions $s_1,\ldots,s_n$ - that means the molecule is stable. The $j$-th atom we assign a $3$-dimensional euclidean space $E_j(=\R^3)$ and put $E\colon=E_1\oplus\cdots\oplus E_n(=\R^{3n})$. Let $x_1\in E_1,\ldots,x_n\in E_n$ be small perturbations of the atoms, so that the $j$-th atoms is located at $s_j+x_j$, then putting
$$
X\colon=(x_1,\ldots,x_n)
=(x_{11},x_{12},x_{13},x_{21},\ldots,x_{n3})
=(X_1,\ldots,X_{3n})\in\R^{3n}:
$$
we get by Taylor's Theorem for sufficiently small perturbations $x_j$:
$$
V(X)=V(x_1,\ldots,x_n)
\sim V_0+\tfrac12\Hess V(0,\ldots,0)(X,X)
=V_0+\tfrac12\la X,HX\ra
$$
where $V_0=V(0,\ldots,0)$, $H$ is a positive linear operator on $E$ and $\la.,.\ra$ the canonical euclidean product on $E=\R^{3n}$, i.e. $H$ is self-adjoint and for all $X\in E$: $\la HX,X\ra\geq0$. The latter property follows from the fact that $V$ attains a local minimum at $X=(0,\ldots,0)$. Elements $X\in E$ essentially represent the positions of the atoms and are therefore called configurations, making $E$ the configuration space.
We try to sidestep partial derivatives, which are a last resort! Since the Taylor expansion of $(1+x^2)^{-2}$ up to order $2$ is given by $1-2x^2$, we get $V(X)=-1+2\sum X_j^2+\cdots$ and thus $HX=4X$.
A motion of the molecule is just a smooth curve $X:\R\rar E$ describing the positions of the atoms over time. For simplicity's sake let us assume that all atoms have the same mass, then the classical equation of motion (cf. example) gives us the following linear differential equation: $X^\dprime(t)=-HX(t)$, which has the unique solution:
$$
X(t)=\cos(t\sqrt H)X(0)+\frac{\sin(t\sqrt H)}{\sqrt H}X^\prime(0)~.
$$
where $\sqrt H$ is the unique positive linear operator $A$ that comes up to $A^2=H$. The operator $\sin(t\sqrt H)/\sqrt H$ is defined by power series expansion of the analytic function $\sin(tz)/z$ replacing $z$ with $\sqrt H$. In our context the uniqueness is not that significant, it's more important to know how to calculate $\sqrt H$:
The roots of the eigen-values of $H$ are called the eigen-frequencies of the molecule, cf wikipedia. An important tool for computing the eigen-spaces of $H$ (or modes, as a physicist would put it) is the group of symmetries $G$ of the molecule: Recall, a symmetry $g\in G$ just permutes the atoms, thus we may think of it as a permutation $j\mapsto\pi(j)$ assigning each displacement vector $x_j$ of the $j$-th atom the displacement vector $g(x_j)$ of the $\pi(j)$-th atom. Now, putting
$$
\Prn_k(\Psi(g)X)
\colon=\d_{k\pi(j)}g(\Prn_j(X))
$$
we get an isometry $\Psi(g)$ of $E$ and it's pretty obvious that $\Psi(g)\in\OO(E)$ and for all $g,h\in G$: $\Psi(gh)=\Psi(g)\Psi(h)$, to state it differently: $\Psi$ is a homomorphism of the group $G$ into the group $\OO(E)$ of isometries of $E$, i.e. $\Psi$ is an orthogonal representation of $G$ in $E$ and a fortiori a unitary representation in $\C^{3n}$ - we will explicate this in more detail when discussing vibrations of $\chem{H_2O}$ and $\chem{CH_4}$ below. Since $G$ is the group of symmetries of the molecule, we hypothesize that the potential energy doesn't change under $\Psi(g)$, i.e.: $V(\Psi(g)X)=V(X)$. This is of course not a statement that can be proved, it's rather an assumption that can be made plausible. In our context it's equivalent (cf. lemma) to the statement:
\begin{equation}\label{mvi1}\tag{MVI1}
\forall g\in G:\qquad
H\Psi(g)=\Psi(g)H
\end{equation}
i.e. the operator $H$ commutes with all isometries $\Psi(g)$, $g\in G$.
Approximate stable states
Remarkably a variety of problems in QM comes down to the same mathematical problem: suppose $n$ electrons, which only interact electrically, are bound by some molecule. What are the "stable states" of the $n$ electrons in the vicinity of positions $s_1,\ldots,s_n\in\R^3$ with minimal electric potential (we assume the atoms are pinned down, thus in this problem $x_1,\ldots,x_n$ are dislocations of the electrons, not of the atoms): approximating the electric potential by its second order Taylor polynomial we have to solve Schrödinger's eigen-equation on $E=\R^{3n}$:
\begin{equation}\label{mvi2}\tag{MVI2}
-\D\psi(X)+\tfrac12\la X,HX\ra\psi(X)=(E-V_0)\psi(X),
\end{equation}
where $V_0\colon=V(0,\ldots,0)$ and $E$ is the energy of the state - mathematically speaking: $\psi$ is an eigen-function and $E-V_0$ the corresponding eigen-value. To solve it, we only need to find the eigen-vectors and eigen-values of $H$; once we've got them, the eigen-functions $\psi$ are well known: Hermite polynomials multiplied by a Gaussian. If $\psi\in L_2(\R^{3n})$ is a normalized solution of \eqref{mvi2}, i.e. $\int|\psi|^2=1$, then the function $X\mapsto|\psi(X)|^2$ is a probability density and $|\psi(x_1,x_2,\ldots,x_n)|^2$ is the probability density for finding one electron in position $s_1+x_1$, another in position $s_2+x_2$ and so on! The stable state with the lowest energy $E$ is called the ground state; mathematically it's the eigen-function with lowest eigen-value!
This just needs two lines in maxima: enter
diff(-exp(-a*x^2),x,2)+4*a^2*x^2*exp(-a*x^2);
diff(-x*exp(-a*x^2),x,2)+4*a^2*x^3*exp(-a*x^2);
and you will see that these two functions are indeed eigen-functions with eigen-values $2a$ and $6a$, respectively.
Vibrations of $\chem{H_2O}$
We assume that the molecule lies in the $yz$-plane (cf. subsection).
Both the $C_2$ rotation and the reflection $\s_1$ interchange the hydrogen atoms and thus the matrix of the site-representation of these symmetries is
$$
\left(\begin{array}{cc}
0&1\\
1&0
\end{array}\right)
$$
To get the matrices of $\Psi(C_2)$ and $\Psi(\s_1)$ we just have to substitute the matrices of $C_2$ and $\s_1$, respectively, for $1$ in the above matrix; this gives us two block matrices:
$$
\left(\begin{array}{cc}
0 &C_2\\
C_2& 0
\end{array}\right),
\left(\begin{array}{cc}
0&\s_1\\
\s_1&0
\end{array}\right),
$$
which are tensor products - cf. section;
in unblocked form they are given by
$$
\left(\begin{array}{cccccc}
0 & 0&0&-1& 0&0\\
0 & 0&0& 0&-1&0\\
0 & 0&0& 0& 0&1\\
-1& 0&0& 0& 0&0\\
0 &-1&0& 0& 0&0\\
0 & 0&1& 0& 0&0
\end{array}\right),
\left(\begin{array}{cccccc}
0& 0&0&1& 0&0\\
0& 0&0&0&-1&0\\
0& 0&0&0& 0&1\\
1& 0&0&0& 0&0\\
0&-1&0&0& 0&0\\
0& 0&1&0& 0&0
\end{array}\right)
$$
The reflection $\s_2$ leaves both hydrogen atoms invariant and therefore the matrix of $\Psi(\s_2)$ is given by
$$
\left(\begin{array}{cc}
\s_2&0\\
0&\s_2
\end{array}\right)
=\left(\begin{array}{cccccc}
-1& 0&0& 0& 0&0\\
0& 1&0& 0& 0&0\\
0& 0&1& 0& 0&0\\
0& 0&0&-1& 0&0\\
0& 0&0& 0& 1&0\\
0& 0&0& 0& 0&1
\end{array}\right)
$$
Vibrations of tetrahedral molecules like methane $\chem{CH_4}$
We retain the notation from subsection.
Fixing the central $C$-atom and labeling the surrounding $H$ atoms $1,2,3,4$ we see that $g\in\{E,C_3,C_2,S_4,\s\}$ permutes the hydrogen atoms as follows:
$$
E:(1234),\quad
C_3:(1342),\quad
C_2:(3412),\quad
S_4:(2341),\quad
\s:(2134)~.
$$
These give rise to associated permutation matrices in $\OO(4)$ - the site representation of $\chem{CH_4}$ (disregarding the central $C$ atom):
$$
\left(\begin{array}{cccc}
1 & 0& 0& 0\\
0 & 0& 0& 1\\
0 & 1& 0& 0\\
0 & 0& 1& 0
\end{array}\right),
\left(\begin{array}{cccc}
0 & 0& 1& 0\\
0 & 0& 0&1\\
1& 0& 0& 0\\
0 &1& 0& 0
\end{array}\right),
\left(\begin{array}{cccc}
0 & 0& 0&1\\
1& 0& 0& 0\\
0 &1& 0& 0\\
0 & 0&1& 0
\end{array}\right),
\left(\begin{array}{cccc}
0 & 1& 0& 0\\
1 & 0& 0& 0\\
0 & 0& 1& 0\\
0 & 0& 0& 1
\end{array}\right)~.
$$
Thus we get an orthogonal representation of $T_d$ in $\R^{12}$ and a fortiori a unitary representation of $T_d$ in $\C^{12}$. We write out the matrices of $\Psi(C_3)$, $\Psi(C_2)$, $\Psi(S_4)$ and $\Psi(\s)$ in block form:
$$
\left(\begin{array}{cccc}
C_3& 0& 0& 0\\
0 & 0& 0&C_3\\
0 &C_3& 0& 0\\
0 & 0&C_3& 0
\end{array}\right),
\left(\begin{array}{cccc}
0 & 0&C_2& 0\\
0 & 0& 0&C_2\\
C_2& 0& 0& 0\\
0 &C_2& 0& 0
\end{array}\right),
\left(\begin{array}{cccc}
0 & 0& 0&S_4\\
S_4& 0& 0& 0\\
0 &S_4& 0& 0\\
0 & 0&S_4& 0
\end{array}\right),
\left(\begin{array}{cccc}
0 & \s& 0& 0\\
\s & 0& 0& 0\\
0 & 0& \s& 0\\
0 & 0& 0& \s
\end{array}\right)~.
$$
Again, these are just the tensor products of the permutation matrices of the site representation and the symmetries itself, cf. section.
The following series of maxima commands will essentially do it:
s: matrix([0,0,-1],[0,1,0],[-1,0,0]);
n: zeromatrix(3,3);
A: matrix([n,s,n,n],[s,n,n,n],[n,n,s,n],[n,n,n,s]);
a: mat_unblocker(A);
eigenvectors(a);
or in sage:
s=matrix([[0,0,-1],[0,1,0],[-1,0,0]])
a=block_matrix([[0,s,0,0],[s,0,0,0],[0,0,s,0],[0,0,0,s]])
a.eigenvalues()
a.eigenspaces_right()
instead of the last two commands you may use:
a.eigenmatrix_right()
or by means of the NumPy library in sage:
import numpy
E,V=numpy.linalg.eig(a)
print(E);print(V)
In any case: the eigen-values are $-1$ ($5$-fold) and $+1$ ($7$-fold) and the eigen-vectors are the columns of the following matrix:
$$
\left(\begin{array}{cccccccccccc}
1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & -1 & 0
\end{array}\right)
$$
Computing eigenvalues exactly in sage
Usually the unitary matrices $U$ we will run across have finite order, i.e. there is some $n\in\N$ such that $U^n=1$. To compute its eigen-values exactly in sage you may possibly consider this matrices as matrices over the cyclotomic field $\Q(e^{2\pi i/N})$ - the field generated by $\Q$ and the complex number $e^{2\pi i/N}$, also known as the cyclotomic field $\Q(e^{2\pi i/N})$ of order $N$, where $N$ is some suitable multiple of $n$:
The order of the matrix is $6$ and since all the entries of the matrix are certainly elements of $\Q(e^{2\pi i/6})$, we choose the cyclotomic field of order $6$:
F.<zeta>=CyclotomicField(6)
U=matrix(F,[[0,1,0,0,0],[0,0,0,0,1],[0,0,0,1,0],[0,0,1,0,0],[1,0,0,0,0]])
U.eigenspaces_right()
This will give you the eigen-values: $\z-1,-\z,-1,1,1$, where $\z=e^{2\pi i/6}$ and the corresponding eigen-vectors, which we omit.
The order of the matrix is $3$ but $i$ is not an element of $\Q(e^{2\pi i/3})$, thus we choose the cyclotomic field of order $12$ because this field contains both $e^{2\pi i/3}$ and $\pm i$:
F.<zeta>=CyclotomicField(12)
U=matrix(F,[[0,I,0],[0,0,1],[-I,0,0]])
U.eigenspaces_right()
The eigen-values of $U$ are: $1,\z^2-1,-\z^2$ where $\z=e^{2\pi i/12}$. The eigen-values must be numbers in $\Q(e^{2\pi i/3})$, indeed: $\z^2-1=e^{2\pi i/3}$ and $-\z^2=e^{4\pi i/3}$.