← Homogene Räume → Hilbert-Transformation

Absolute Konvergenz und Konvergenz f.ü.

Fourierreihen in $L_1(\TT)$ und $C(\TT)$

Wir zeigen zunächst, daß es eine integrierbare (bzw. stetige) Funktion $f:\TT\rar\R$ gibt, so daß die symmetrischen Partialsummen $S_n(f)$ in $L_1(\TT)$ (bzw. $C(\TT)$) nicht gegen $f$ konvergieren. Da $$ \norm{S_n:L_1(\TT)\rar L_1(\TT)} =\norm{S_n:C(\TT)\rar C(\TT)} =\norm{D_n}_1, $$ genügt es nach Korollar folgende Proposition zu zeigen:
Es gilt: $$ \lim_n\frac{\norm{D_n}_1}{\log n}=\frac4{\pi^2}~. $$
$\proof$ Da für $0 < t <\pi/2$: $0\leq1/\sin(t)-1/t\leq c$, folgt wegen $D_n(t)=D_n(-t)$ und (DFP2): \begin{eqnarray*} \norm{D_n}_1 &=&\frac1{\pi}\int_0^{\pi}|D_n(t)|\,dt =\frac2{\pi}\int_0^{\pi/2}\frac{|\sin((2n+1)t)|}{\sin(t)}\,dt\\ &=&\frac2{\pi}\int_0^{\pi/2}\frac{|\sin((2n+1)t)|}{t}\,dt+\Oh(1) \end{eqnarray*} Für das letzte Integral erhalten wir mit der Substitution $x=(2n+1)t$: $$ \frac2{\pi}\int_0^{(2n+1)\pi/2}\frac{|\sin x|}{x}\,dx =\frac2{\pi}\sum_{k=0}^{2n}\int_{k\pi/2}^{(k+1)\pi/2}\frac{|\sin x|}{x}\,dx =\frac2{\pi}\sum_{k=0}^{2n}\int_{0}^{\pi/2}\frac{u_k(x)}{k\pi/2+x}\,dx $$ wobei $u_k(x)=\sin x$, falls $k$ gerade ist und $u_k(x)=\cos x$ für ungerade $k$. Jedenfalls ist $\int_0^{\pi/2}u_k(x)\,dx=1$ und für $k\geq1$: $$ \frac4{\pi^2(k+1)}\int_{0}^{\pi/2}u_k(x)\,dx \leq\frac2{\pi}\int_{0}^{\pi/2}\frac{u_k(x)}{k\pi/2+x} \leq\frac4{\pi^2k}\int_{0}^{\pi/2}u_k(x)\,dx $$ Da $\int_0^{\pi/2} u_0(x)/x\,dx$ endlich ist und $\sum_{k=1}^n1/k=\log n+\Oh(1)$, folgt die Behauptung. $\eofproof$
Die Fouriertransformation $\F$ bildet $L_1(\TT)$ auf einen dichten Teilraum von $c_0(\Z)$ ab. Die folgende Proposition zeigt u.a., daß wir nicht negative integrierbare Funktionen mit dieser Eigenschaft finden können, deren Fpourierkoeffizienten 'beliebig' langsam gegen $0$ konvergieren (vgl. Korollar).
Sei $a\in c_0(\Z)$, so daß für alle $n\in\N$ $$ a(-n)=a(n)\geq0 \quad\mbox{und}\quad a(n)\leq\tfrac12(a(n-1)+a(n+1))~. $$ Dann existiert eine nicht negative integrierbare Funktion $f$, so daß $\wh f=a$.
$\proof$ Die Bedingungen an $a$ implizieren, daß die Folge $a(n)-a(n+1)$ monoton fällt und daß $n(a(n+1)-a(n))$ eine Nullfolge ist, denn für alle $n\in\N$ ist $$ a(n)-a(0)=\sum_{k=1}^n a(k)-a(k-1)\geq n(a(n)-a(n-1)) $$ Daher folgt mit $b(n)\colon=a(n)-a(n-1)$ nach Abel-Summation (cf. Lemma mit $w_k=b(k)$ und $z_k=1$): \begin{eqnarray*} \sum_{k=1}^\infty k(a(k-1)+a(k+1)-2a(k)) &=&-\lim_{n\to\infty}\sum_{k=1}^n k(b(k)-b(k+1))\\ &=&-\lim_{n\to\infty}0\cdot b(1)-nb(n+1)+\sum_{k=1}^n b(k)\\ &=&\lim_{n\to\infty}nb(n+1)+a(0)-a(n) =a(0)~. \end{eqnarray*} Sind $K_k$ die Fejer-Kerne, so ist durch $$ f(t)\colon=\sum_{k=1}^\infty n(a(k-1)+a(k+1)-2a(k))K_{k-1}(t) $$ eine nicht negative integrierbare Funktion definiert und es gilt wegen $\wh K_k(m)=0$ für $|m|>k$ nach (DFP4) und wiederum Lemma: \begin{eqnarray*} \wh f(m)&=&\sum_{k=1}^\infty k(a(k-1)+a(k+1)-2a(k))\wh K_{k-1}(m)\\ &=&\sum_{k=m+1}^\infty k(a(k-1)+a(k+1)-2a(k))(1-m/k)\\ &=&\sum_{k=m+1}^\infty k(b(k+1)-b(k))-m\sum_{k=m+1}^\infty (b(k+1)-b(k))\\ &=&\lim_{n\to\infty}-mb(m+1)+nb(n+1)+a(m)-a(n) +\lim_{n\to\infty}-mb(n+1)+mb(m+1) =a(m)~. \end{eqnarray*} Für $m < 0$ folgt die Behauptung aus der Symmetrie von $a$ und $\wh K_k$. $\eofproof$
Ist $a:\R_0^+\rar\R_0^+$ eine monoton fallende konvexe Funktion, so erfüllt die Folge $a(|n|)$ die Voraussetzungen von Proposition.
Zu jedem $\a > 0$ gibt es eine nicht negative integrierbare Funktion $f$ mit $\wh f(n)=|n|^{-\a}$.
Es gibt eine nicht negative integrierbare Funktion $f$ mit $\wh f(n)=|1/\log(n)|$.

Absolut konvergente Fourierreihen

 Der Raum $A(\TT)\colon=\{f\in L_1(\TT): \sum|\wh f(n)|<\infty\}$ mit der Norm \begin{equation}\label{akfeq1}\tag{AKF1} \norm f_{A(\TT)}\colon=\sum_{n\in\Z}|\wh f(n)| \end{equation} ist ein zu $\ell_1(\Z)$ isometrisch isomorpher Banachraum und jede Funktion in $A(\TT)$ ist stetig, genauer: die kanonische Injektion $A(\TT)\hrar C(\TT)$ ist stetig, denn ihre Fourierreihe konvergiert gleichmäßig; ferner gilt: $\norm f_\infty\leq\norm f_{A(\TT)}$.
Man nennt für $a,b\in\ell_1(\Z)$ die durch $n\mapsto\sum_{k\in\Z}a(k)b(n-k)$ definierte Abbildung die Faltung von $a$ und $b$ und bezeichnet sie mit $a*b$. Die Faltung zweier endlicher Maße läßt sich auf einfache Weise auf topologischen Gruppen $G$ analog zu (FHB1) definieren: $$ \forall A\in\B(G):\qquad \mu*\nu(A)\colon=\int\mu(Ag^{-1})\,\nu(dg) =\int\nu(g^{-1}A)\,\mu(dg) $$ Die Faltung zweier Funktionen setzt jedoch ein Referenzmaß voraus und dafür wählt man i.A. ein sogenanntes linksinvariantes Haarmaß, d.h. ein Radonmaß $m$ mit der Eigenschaft, daß für alle kompakten Teilmengen $K$ von $G$ und alle $x\in G$: $m(xK)=m(K)$. Ein solches Maß existiert, wenn $G$ z.B. lokalkompakt ist. Im Falle einer diskreten Gruppe ist $m$ das Zählmaß, das dann auch rechtsinvariant ist, also $m(Kx)=m(K)$) Cf. Harmonische Analysis auf lokalkompakten Gruppen.
$A(\TT)$ ist mit der punktweisen Multiplikation von Funktionen eine kommutative Banachalgebra mit Eins. Genauer: Für $f,g\in A(\TT)$ gilt: $\wh{fg}=\wh f*\wh g$.
$\proof$ Die Eins ist die konstante Funktion $e_0:t\mapsto 1$. Wir haben zu zeigen, daß für $f,g\in A(\TT)$ gilt: $\norm{fg}_{A(\TT)} \leq\norm f_{A(\TT)}\norm g_{A(\TT)}$. Seien also $$ f(t)=\sum_{n\in\Z}\wh f(n)e^{int} \quad\mbox{und}\quad g(t)=\sum_{n\in\Z}\wh g(n)e^{int} $$ Da beide Reihen absolut konvergieren, existiert das Cauchy Produkt beider Reihen und es folgt: $$ f(t)g(t)=\sum_k\sum_m\wh f(k)\wh g(m)e^{i(k+m)t} =\sum_{n\in\Z}\Big(\sum_{k\in\Z}\wh f(k)\wh g(n-k)\Big)e^{int} $$ Somit gilt: $\wh{fg}(n)=\sum_{k\in\Z}\wh f(k)\wh g(n-k)=\wh f*\wh g(n)$ und daraus erhalten wir: $$ \sum_{k\in\Z}|\wh{fg}(n)| \leq\sum_n\sum_k|\wh f(k)\wh g(n-k)| =\sum_k|\wh f(k)|\sum|\wh g(m)| =\norm f_{A(\TT)}\norm g_{A(\TT)}~. $$ $\eofproof$
Wir bemerken, daß für $g(t)=\cl{f(t)}$: $\wh g(n)=\cl{\wh f(-n)}$.
Sei $f,g\in\ell_1(\Z)$, dann ist $K:g\rar f*g$ eine lineare Abbildung von $\ell_1(\Z)$ in sich mit der adjungierten $K^*(g)=\check f*g$ mit $\check f(n)=\bar f(-n)$. Vgl. exam!
Für $s > 1/2$ ist die kanonische Injektion $H^s(\TT)\hrar A(\TT)$ stetig.
$\proof$ Es gilt $\norm f_{H^s}^2=\sum_{n\in\Z}|\wh f(n)|^2(1+n^2)^s$, also nach der Cauchy-Schwarz Ungleichung: $$ \sum_n|\wh f(n)| =\sum_n|\wh f(n)|(1+n^2)^{s/2}(1+n^2)^{-s/2} \leq\norm f_{H^s}\Big(\sum_n(1+n^2)^{-s}\Big)^{1/2}~. $$ $\eofproof$
Sei $X$ ein kompakter metrischer Raum und $\a\in(0,1]$. $\lip_\a(X)$ ist der Raum aller Funktionen $f\in C(X)$, für die \begin{equation}\label{akfeq2}\tag{AKF2} \norm f_{\lip_\a}\colon=\norm f_\infty +\sup\Big\{\Big|\frac{f(x)-f(y)}{d(x,y)^\a}\Big|:x,y\in X,x\neq y\Big\} <\infty \end{equation} Der Raum $\lip_\a(\TT)$ ist kein homogener Banachraum, denn er verletzt die Bedingung (IV). Nach dem Dini-Test konvergiert die Fourierreihe jeder Funktion $f\in\lip_\a(\TT)$ in allen Punkten gegen $f$. Der folgende Satz zeigt, daß die Fourierreihe einer Funktion $f\in\lip_\a(\TT)$ für $\a > 1/2$ absolut konvergiert.
Die kanonische Injektion $\lip_\a(\TT)\hrar A(\TT)$ ist für alle $\a > 1/2$ stetig.
$\proof$ Für alle $\theta\in\TT$ und $t > 0$ gilt: $$ f(\theta-t)-f(\theta) =L_tf(\theta)-f(\theta) =\sum_{n\in\Z}(e^{-int}-1)\wh f(n)e^{in\theta}~. $$ Sei $A(t)\colon=\{n\in\Z:\frac12\pi\leq|nt| < \pi\}$, dann folgt für alle $n\in A(t)$: $|e^{-int}-1|\geq\sqrt2$. Nach der Parsevalschen Gleichung erhalten wir also: \begin{eqnarray*} \sum_{n\in A(t)}|\wh f(n)|^2 &\leq&\tfrac12\sum_{n\in A(t)}|e^{-int}-1|^2|\wh f(n)|^2 \leq\tfrac12\sum_{n\in\Z}|e^{-int}-1|^2|\wh f(n)|^2\\ &=&\tfrac12\norm{L_tf-f}_2^2 \leq\tfrac12\norm{L_tf-f}_\infty^2 \leq\tfrac12t^{2\a}\norm{f}_{\lip_\a}^2 \end{eqnarray*} Sei $n\in A(t)$, dann ist $\tfrac12\pi/t\leq |n| < \pi/t$, also folgt für die Mächtigkeit $N(t)$ von $A(t)$: $N(t)\leq\pi/t$. Nach der Ungleichung zwischen arithmetischem und quadratischem Mittel erhalten wir: \begin{eqnarray*} \sum_{n\in A(t)}|\wh f(n)| &\leq&\Big(N(t)\sum_{n\in A(t)}|\wh f(n)|^2\Big)^{1/2}\\ &\leq&\sqrt{\tfrac12N(t)}\,t^{\a}\norm{f}_{\lip_\a} \leq\sqrt{\tfrac12\pi}\,t^{\a-1/2}\norm{f}_{\lip_\a}~. \end{eqnarray*} Somit gilt für alle $k\in\Z$: $$ \sum_{n\in A(t/2^k)}|\wh f(n)| \leq\sqrt{\tfrac12\pi}\,t^{\a-1/2}\norm{f}_{\lip_\a}2^{-(\a-1/2)k}~. $$ Da $A(t/2^k)=\{n\in\Z:2^{k-1}\pi\leq|nt| < 2^k\pi\}$, $k\geq\log_2(2t/\pi)$, eine Zerlegung von $\Z\sm\{0\}$ ist, folgt mit $\b\colon=\a-1/2 > 0$: \begin{eqnarray*} \sum_{n\in\Z\sm\{0\}}|\wh f(n)| &\leq&\sqrt{\tfrac12\pi}\,t^{\b}\norm{f}_{\lip_\a} \sum_{k\geq\log_2(2t/\pi)}^\infty 2^{-\b k}\\ &\leq&\sqrt{\tfrac12\pi}\,t^{\b}\norm{f}_{\lip_\a} \frac{2^{-\b\log_2(2t/\pi)}}{1-2^{-\b}} =C(\a)\,\norm{f}_{\lip_\a}~. \end{eqnarray*} $\eofproof$

Der Satz von Bochner

 Sei $\mu\in M(\TT)$ ein komplexwertiges Maß auf $\TT$, dann nennt man die Funktion $\wh\mu:\Z\rar\C$, $$ \wh\mu(n)\colon=\frac1{2\pi}\int e^{-int}\,\mu(dt) $$ die Fourier oder die Fourier-Stieltjes Transformierte von $\mu$. Der Satz von Bochner charakterisiert die Wahrscheinlichkeitsmaße $\mu$ auf $\TT$ durch ihre Fourier-Stieltjes Transformierte $\wh\mu$.
Ist zunächst $\vp\in\ell_1(\Z)$ mit $\vp(0)=1$, dann gibt es eine Funktion $f\in A(\TT)$, so daß $\wh f=\vp$; somit ist $\vp$ genau dann die Fourier-Stieltjes Transformierte eines Wahrscheinlichkeitsmaßes, wenn: \begin{equation}\label{bocheq2}\tag{DSB1} \forall\theta\in\TT:\qquad f(\theta)\colon=\sum_{n\in\Z}\vp(n)e^{in\theta}\geq0~. \end{equation}
Eine Folge $\mu_k$ von Wahrscheinlichkeitsmaßen auf $\TT$ konvergiert genau dann schwach $*$ gegen ein Wahrscheinlichkeitsmaß $\mu$, wenn für alle $n\in\Z$ die Folge $\wh\mu_k(n)$ konvergiert; der Limes $\vp(n)$ dieser Folge ist dann die Fourier-Stieltjes Transformierte von $\mu$.
$\proof$ Setzen wir $\la f,\mu\ra\colon=\int f\,d\mu$, so folgt: $$ \wh\mu_k(n)=(2\pi)^{-1}\la e_{-n},\mu\ra~. $$ Offensichtlich konvergiert für alle $n\in\Z$ die Folge $\wh\mu_k(n)$ gegen $\wh\mu(n)$, wenn $\mu_k$ schwach * gegen $\mu$ konvergiert.
Konvergiere umgekehrt die Folge $\la f,\mu_k\ra$ für jedes trigonometrische Polynom $f\in{\cal A}$. Nach dem Banach-Alaoglu Theorem sowie dem Rieszschen Darstellungssatz gibt es eine Teilfolge $\mu_{k(m)}$, die schwach $*$ gegen ein $\mu\in M(\TT)$ konvergiert. Da $\mu_k$ Wahrscheinlichkeitsmaße sind, ist auch $\mu$ ein Wahrscheinlichkeitsmaß. Ferner gilt: $$ \forall n\in\Z:\quad \lim_k\wh\mu_k(n) =\lim_m\wh\mu_{k(m)}(n) =(2\pi)^{-1}\la e_{-n},\mu\ra =\wh\mu(n)~. $$ Nun ist ${\cal A}$ dicht in $C(\TT)$, und damit konvergiert $\la f,\mu_k\ra$ für alle $f\in C(\TT)$ gegen $\la f,\mu\ra$, denn zu $\e > 0$ wähle $p\in{\cal A}$ mit $\norm{f-p} < \e$; es folgt: $$ \limsup_k|\la f,\mu_k\ra-\la f,\mu\ra| \leq\limsup_k|\la f,\mu_k\ra-\la p,\mu_k\ra| +\limsup_k|\la p,\mu_k\ra-\la p,\mu\ra| +\limsup_k|\la p,\mu\ra-\la f,\mu\ra|\\ \leq\e+0+\e, $$ $\eofproof$
Sei $\vp\in\ell_\infty(\Z)$ mit $\vp(0)=1/2\pi$. $\vp$ ist genau dann die Fourier-Stieltjes Transformierte eines Wahrscheinlichkeitsmaßes, wenn $$ \forall r < 1\ \forall\theta\in\TT:\qquad f_r(\theta)\colon=\sum_{n\in\Z}\vp(n)r^{|n|}e^{in\theta}\geq0~. $$
$\proof$ 1. Sei $\mu$ ein Wahrscheinlichkeitsmaß und $P(r,.)$ der Poissonkern $$ P(r,\theta)=\sum_{n\in\Z}r^{|n|}e^{in\theta}=\frac{1-r^2}{1-2r\cos\theta+r^2}~. $$ Dann folgt $f_r=P(r,.)*\mu$, denn $\wh f_r(n)=\vp(n)r^{|n|}$ und somit $f_r(\theta)\geq0$.
2. Zu jedem $r < 1$ ist $\mu_r(d\theta)\colon=f_r(\theta)\,d\theta$ ein Wahrscheinlichkeitsmaß mit $\wh\mu_r(n)=r^{|n|}\vp(n)$. Nach Lemma ist dann auch $\vp$ die Fourier-Stieltjes Transformierte eines Wahrscheinlichkeitsmaßes. $\eofproof$
Dem Poissonkern kommt im voranstehenden Resultat keine besonder Bedeutung zu: Sei $\mu$ ein Wahrscheinlichkeitsmaß auf $\TT$ mit der Fourier-Stieltjes Transformierten $\vp$ und $a\in\ell_1(\Z)$, dann gilt die sogenannte Parsevalsche Relation: $$ \sum_{n\in\Z}\vp(n)a(n)e^{in\theta} =\frac1{2\pi}\sum_{n\in\Z}\int a(n)e^{in(\theta-t)}\,\mu(dt) =\frac1{2\pi}\int h(\theta-t)\,\mu(dt) $$ wobei $h\in A(\TT)$ definiert ist durch $\wh h(n)=a(n)$. Ist nun $b=a*a^*$, wobei $a^*(n)\colon=\cl{a(-n)}$, dann folgt nach der Bemerkung zu Proposition: $$ \sum_{n\in\Z}b(n)e^{in\theta}=|h(\theta)|^2~. $$ Daher gilt für alle $a\in\ell_1(\Z)$: $$ \sum_{n\in\Z}\vp(n)a*a^*(n)e^{in\theta} =\frac1{2\pi}\int|h(\theta-t)|^2\,\mu(dt)\geq0~. $$ Setzen wir $h\colon=\sqrt{P_r}\in C^\infty(\TT)$, so folgt $h\in A(\TT)$ und nach Proposition: $a*a^*(n)=\wh{h^2}(n)=\wh{P_r}(n)=r^{|n|}$. Nach Proposition ist daher $\vp\in\ell_\infty(\Z)$ mit $\vp(0)=1/2\pi$ genau dann die Fourier-Stieltjes Transformierte eines Wahrscheinlichkeitsmaßes, wenn für alle $a\in A(\TT)$: \begin{equation}\label{bocheq1}\tag{DSB2} \sum_{n\in\Z}\vp(n)a*a^*(n)e^{in\theta}\geq0~. \end{equation} Besitzt $a$ endliche Träger, also z.B. $n_1,\ldots,n_N\in\Z$ und setzen wir $c_j\colon=a(n_j)e^{in_j\theta}$, so besagt \eqref{bocheq1} nach exam: $$ \sum_{j,k=1}^N\vp(n_j-n_k)e^{i(n_j-n_k)t}a(n_j)a(n_k) =\sum_{j,k=1}^N\vp(n_j-n_k)c_j\bar c_k =\int\Big|\sum_{j=1}^N c_je^{in_jt}\Big|^2\,\mu(dt) \geq0~. $$
Eine Funktion $\vp:\Z\to\C$ heißt positiv definit, falls für alle $N\in\N$, alle $c_1,\ldots,c_N\in\C$ und alle $n_1,\ldots,n_N\in\Z$: $$ \sum_{j,k=1}^Nc_j\bar c_k\vp(n_j-n_k)\geq0~. $$
$\vp:\Z\rar\C$ mit $\vp(0)=1/2\pi$ ist genau dann die Fourier-Stieltjes Transformierte eines Wahrscheinlichkeitsmaßes, wenn $\vp$ positiv definit ist
$\proof$ Nach Proposition genügt es zu zeigen, daß jede positiv definite Funktion beschränkt ist. Wir zeigen, daß für jede positiv definite Funktion $\vp:\Z\rar\C$ gilt:
  1. $\vp(-n)=\cl{\vp(n)}$.
  2. $|\vp(n)|\leq\vp(0)$.
1. Zunächst ist $\vp(0)\geq0$. Für $N=2$, $n_1=0$, $n_2=n$, $c_1=1$ und $c_2=z\in\C$ folgt: \begin{equation}\label{bocheq3}\tag{DSB3} (1+|z|^2)\vp(0)+z\vp(n)+\bar z\vp(-n)\geq0~. \end{equation} Setzen wir $z=1$, so folgt: $\Im\vp(-n)=-\Im\vp(n)$, und für $z=i$ folgt: $\Re\vp(-n)=\Re\vp(n)$.
2. Setzen wir $z=-|\vp(n)|/\vp(n)$ so erhalten wir nach \eqref{bocheq3} und 1.: $2\vp(0)-2|\vp(n)|\geq0$. $\eofproof$

Maximalfunktion und f.ü. Konvergenz

Für $f\in L_1(\TT)$ heißt die durch \begin{equation}\label{maxeq0}\tag{MAX1} f^*(\theta)\colon=\sup_{t>0}\frac1t \int_{\theta-t}^\theta|f(u)|\,d\mu(du) \end{equation} definierte Funktion die Maximalfunktion von $f$ bezüglich $\mu$.
Sei $g:\R_0^+\rar\R$ stetig und $$ U(g)=\{x\in\R^+:\,\exists y < x \quad g(y) < g(x)\}~. $$ Dann ist $U(g)$ die abzählbare Vereinigung paarweise disjunkter offener Intervalle $I_n=(a_n,b_n)$. Falls $b_n < \infty$, dann gilt: $g(a_n)=g(b_n)$ und falls $b_n=\infty$, dann gilt: $g(a_n)=\inf\{g(b):b\geq a_n\}$.
$\proof$ In unserem Fall geht die Sonne auf der linken Seite von oben nach unten auf und bescheint alle jene Punkte $(x,g(x))$ - im Bild rot dargestellt - des Graphs von $g$, für die $x$ im Komplement von $U(g)$ liegt. Die Punkte $x$ für die $(x,g(x))$ im Schatten liegt - im Bild blau dargestellt - sind genau die Punkte aus $U(g)$.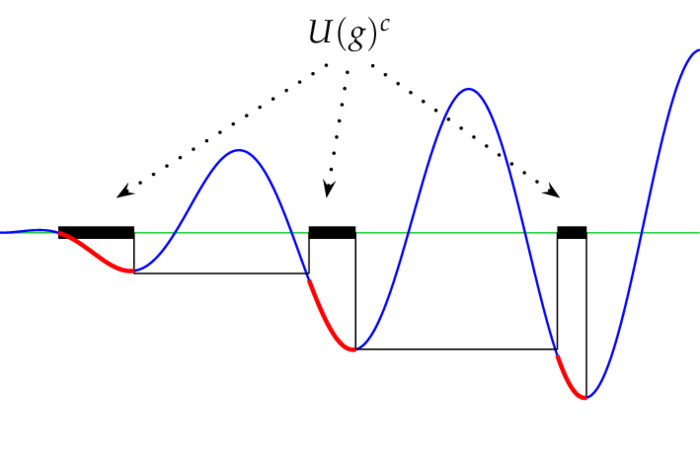
rising sun
$U(g)$ is offen und folglich höchstens abzählbare Vereinigung von paarweise disjunkten offenen Intervallen $(a_n,b_n)$, i.e. $U(g)=\bigcup(a_n,b_n)$. Angenommen $b_n < \infty$ und $g(a_n) < g(b_n)$, dann folgt: $b_n\in U(g)$, also muß gelten: $g(a_n)\geq g(b_n)$.
Umgekehrt folgt aus $(a,b]\sbe U(g)$: $g(a) < g(b)$, denn andernfalls wäre $g(a)\geq g(b)$ und $g$ nähme auf $(a,b]$ ein Minimum in $c\in(a,b]$ an und somit gibt es ein $d < c$ mit $g(d) < g(c)$. Falls $d\leq a$, dann folgt aber: $g(a)\geq g(c) > g(d)$, i.e. $a\in U(g)$. Es gilt also $d > a$, also $d\in(a,b]$ und $g(d) < g(c)$; $g$ nimmt also auf $(a,b]$ ihr Minimum nicht in $c$ an.
Falls $(a,\infty)\in U(g)$, dann gilt für alle $b > a$: $g(a) < g(b)$ und damit: $g(a)=\inf\{g(b):b > a\}$. $\eofproof$
Für alle $f\in L_1(\R^+)$ und alle $s > 0$ gilt: $$ s\l(f^* > s)\leq\int_{[f^*>s]}|f|\,d\l~. $$
$\proof$ Sei $s > 0$ und o.B.d.A. $f\geq0$, dann gilt $f^*(\theta) > s$ genau dann, wenn ein $t > 0$ existiert, so daß $$ \int_{\theta-t}^\theta f(u)\,du > st~. $$ Setzen wir $g(\theta)=\int_{(0,\theta]} f(u)-s\,du$, so ist $g$ stetig und $f^*(\theta) > s$ gleichbedeutend mit $$ \exists t > 0:\quad g(\theta) > g(\theta-t) \quad\mbox{i.e.}\quad \theta\in U(g) $$ Folglich ist nach dem Rising Sun Lemma: $$ \int_{f^* > s}f-s\,d\mu =\int_{U(g)}f-s\,d\mu =\sum_n\int_{I_n}f-s\,d\mu =\sum_n g(b_n)-g(a_n) \geq0~. $$ $\eofproof$
Die Maximalungleichung impliziert z.B. für jede monoton steigende, stückweise glatte Funktion $\vp:\R_0^+\rar\R_0^+$ mit $\vp(0)=0$ und $\Phi(t)\colon=\int_0^t\vp^\prime(s)s^{-1}\,ds$ nach Fubini: \begin{eqnarray*} \int\vp(f^*)\,d\l &=&\int_0^\infty\vp^\prime(t)\l(f^*>t)\,dt\\ &\leq&\int_0^\infty\vp^\prime(t)t^{-1}\int_{[f^* > t]}|f(s)|\,ds\,dt\\ &=&\int_0^\infty\int_0^{f^*(s)}\vp^\prime(t)t^{-1}|f(s)|\,dt\,ds =\int_0^\infty\Phi(f^*)|f|\,d\l \end{eqnarray*} Für $\vp(t)=t^p$, $p > 1$, folgt: $\Phi(t)=pt^{p-1}/(p-1)$ und damit nach der Hölder Ungleichung mit $1/p+1/q=1$: $$ \int f^{*p}\,d\l \leq\frac p{p-1}\Big(\int f^{*p}\,d\l\Big)^{1/q} \Big(\int|f|^p\,d\l\Big)^{1/p} $$ also \begin{equation}\label{maxeq1}\tag{MAX2} \Big(\int f^{*p}\,d\l\Big)^{1/p} \leq\frac p{p-1}\Big(\int|f|^p\,d\l\Big)^{1/p} \end{equation} Im Weiteren sei $K$ ein Summationskern und $Q_s$ die durch (SUK2) definierten Operatoren. Ferner bezeichne $f^*$ die Maximalfunktion bezüglich des Lebesguemaßes, also \begin{equation}\label{maxeq2}\tag{MAX3} f^*(\theta) =\sup_{t > 0}\frac1{t}\int_{\theta-t}^\theta f(u)\,du =\sup_{t > 0}\frac1{t}\int_0^t f(\theta-s)\,ds =\sup_{t > 0}\frac1{t}\int_0^t L_sf(\theta)\,ds \end{equation}
Ist $K$ ein Summationskern, der (IV) erfüllt, dann gilt für alle $f\in L_1(\TT)$: $$ \sup_{s > 0}|Q_sf(\theta)| \leq f^*(\theta)\frac1{\pi}\int_0^\infty\b(t)\,dt~. $$
$\proof$ Seien o.B.d.A. $K,f\geq0$ und $\vp(t)\colon=\b(t/s)/s$, dann erhalten wir: $$ Q_sf(\theta) =\frac1{2\pi}\int_\TT K(s,t)f(\theta-t)\,dt \leq\frac1{\pi}\int_0^{\pi}\vp(t)L_tf(\theta)\,dt~. $$ Setzen wir $A_tf\colon=\frac1t\int_0^tL_sf\,ds$, so folgt: $\ttd t(tA_tf)=L_tf$ und $A_tf\leq f^*$; mittels partieller Integration (cf. exam) folgt schließlich: \begin{eqnarray*} \int_0^{\pi}\vp(t)L_tf\,dt &=&\int_0^{\pi}\vp(t)\ttd t(tA_tf)\,dt\\ &=&\vp(\pi)\pi A_{\pi}f+\int_0^{\pi}tA_tf(-\vp^\prime(t))\,dt\\ &\leq&f^*\Big(\vp(\pi)\pi-\int_0^{\pi} t\vp^\prime(t)\,dt\Big)\\ &=&f^*\int_0^{\pi}\vp(t)\,dt \leq f^*\int_0^\infty\b(t)\,dt~. \end{eqnarray*} $\eofproof$
Ist $K$ ein Summationskern, der (IV) erfüllt, dann gilt für alle $f\in L_1(\TT)$ und für fast alle $\theta\in\TT$: $$ \lim_{s\dar0}Q_sf(\theta)=f(\theta)~. $$
$\proof$ Sei $f\in C(\TT)$, dann konvergiert $Q_sf$ nach Korollar gleichmäßig und somit punktweise mit $s\dar0$ gegen $f$. Sei nun $f\in L_1(\TT)$ o.B.d.A. nicht negativ, so existiert zu jedem $\e>0$ eine nicht negative Funktion $g\in C(\TT)$, so daß $\norm{f-g}_1\leq\e$. Da $$ \limsup_{s\dar0}|Q_sf-f| \leq\limsup_{s\dar0}|Q_sf-Q_sg|+|g-f|+\limsup_{s\dar0}|Q_sg-g|, $$ erhalten wir nach Lemma bzw. der Chebyshev Ungleichung sowie Satz für alle $t > 0$ mit $C=2\int_0^\infty\b(s)\,ds$: \begin{eqnarray*} \l(\limsup_{s\dar0}|Q_sf-f| > 3t) &\leq&\l(|f-g|^* > t/C)+\l(|f-g| > t)+\l(\limsup_{s\dar0}|Q_sg-g| > t)\\ &\leq&C\norm{f-g}_1/t+\norm{f-g}_1/t+0 \leq\e(C+1)/t~. \end{eqnarray*} Da $\e > 0$ beliebig war, folgt für alle $t > 0$: $\l(\limsup_{s\dar0}|Q_sf-f| > 3t)=0$, i.e. $Q_sf$ konvergiert $\l$-f.ü. gegen $f$. $\eofproof$
Seien $K_m$ bzw. $P_r$ der Fejer- bzw. der Poisson-Kern. Dann gilt für alle $f\in L_1(\TT)$ und fast alle $\theta\in\TT$: $$ \lim_{m\to\infty}K_m*f(\theta)=f(\theta) \quad\mbox{und}\quad \lim_{r\uar1}P_r*f(\theta)=f(\theta) $$
Für alle $f\in L_1(\R)$ ist die Funktion $F(x)\colon=\int_0^x f(t)\,dt$ $\l$-f.ü. differenzierbar und es gilt $\l$-f.ü.: $$ F^\prime(x)=\lim_{t\dar0}\frac{F(x)-F(x-t)}t~. $$

Übungen und ergänzende Resultate
Sei $\l$ das Lebesguemaß auf $\R^{n^2}=\Ma(n,\R)$ - der Menge der reellen $n\times n$-Matrizen. Dann ist $m(dX)\colon=|\det X|^{-n}\,\l(dX)$ ein sowohl links- wie rechtsinvariantes Haarmaß auf der Automorphismengruppe $\Gl(n,\R)$.
Sei $E^{lm}\in\Ma(n,\R)$ jene Matrix, die in der $l$-ten Zeile und $k$-ten Spalte den Eintrag $1$ hat und sonst nur $0$. Für alle $X\in\Gl(n,\R)$ ist $A\mapsto L_XA=XA$ eine lineare Abbildung von $\Ma(n,\R)$. Es gilt: $(XE^{lm})_{jk}=x_{jl}\d_{km}$, also: $$ XE^{lm}=\sum_{j,k}x_{jl}\d_{km}E^{jk} =\sum_{j}x_{jl}E^{jm} $$ Der Betrag der Determinante dieser linearen Abbildung ist daher $|\det X|^n$. Für jede kompakte Teilmenge ${\cal K}$ von $\Gl(n,\R)$ gilt nach dem Transformationssatz: \begin{eqnarray*} m(X{\cal K}) &=&\int_{X{\cal K}}|\det Y|^{-n}\,\l(dY) =\int_{{\cal K}}|\det L_XY|^{-n}|\det DL_X(Y)|\,\l(dY)\\ &=&\int_{{\cal K}}|\det(XY)|^{-n}|\det X|^n\,\l(dY) =\int_{{\cal K}}|\det Y|^{-n}\,\l(dY) =m({\cal K}) \end{eqnarray*} und analog $m({\cal K}X)=m({\cal K})$.
Sei $p > 1$, $b_j>0$ und $a_j\geq0$, dann gilt $$ \sum a_j^pb_j^{1-p}\geq(\sum a_j)^p/(\sum b_j)^{p-1} $$ und Gleichheit gilt genau dann, wenn ein $\l\geq0$ existiert, so daß für alle $j$: $a_j=\l b_j$.
Es gilt für $c_j>0$ und $1/p+1/q=1$: $$ (\sum a_j)^p =(\sum a_jc_j/c_j)^p \leq(\sum a_j^pc_j^{-p})(\sum c_j^{q})^{p/q} $$ Setze $c_j^p=b_j^{p-1}$ d.h. $c_j=b_j^{1/q}$.
Sei $f\in L_\infty(\TT)$ und $|\wh f(n)|\leq K/|n|$; dann gilt für alle $n\in\N$ und alle $t\in(0,2\pi)$: $$ |S_n(f)(t)|\leq\norm f_\infty+2K~. $$
Es ist $$ \s_n(f)(t)=\sum_{|j|\leq n}(1-\tfrac{|j|}{n+1})\wh f(j)e^{ijt} =S_n(f)(t)-\sum_{|j|\leq n}\tfrac{|j|}{n+1}\wh f(j)e^{ijt} $$ also: $$ |S_n(f)(t)| \leq|\s_n(f)(t)|+\sum_{|j|\leq n}\tfrac{|j|}{n+1}|\wh f(j)| \leq\norm f_\infty+\tfrac{2n}{n+1}K $$
Für alle $n\in\N$ und alle $t\in\TT$ gilt: $$ |\sum_{j=1}^n\tfrac1j\sin(jt)|\leq\tfrac12\pi+1 $$
Sei $f(t)\colon=\frac12(\pi-t)$. Die Fourierreihe von $f$ ist $\sum \tfrac1j\sin(jt)$. Da $\norm f_\infty=\pi/2$ und $|\wh f(j)|\leq1/2j$, folgt die Behauptung aus dem voranstehenden Beispiel.
Die Fourierreihe der Funktion $$ f(t)\colon=\sum_{j=1}^\infty 2^{-j}K_{N_j}(t) $$ konvergiert nicht in $L_1(\TT)$ falls die Folge $N_j$ rasch genug gegen $\infty$ konvergiert (z.B. $N_j=2^{2^j}$).
Da $K_n\geq0$ und $\int K_n=1$, folgt $f\geq0$ und $\int f=1$. Ferner ist $$ S_n(f)-\sum_{j:n\geq N_j}2^{-j}K_{N_j} =\sum_{j=1}^\infty 2^{-j}D_n*K_{N_j} =\sum_{j:n < N_j}2^{-j}D_n*K_{N_j} $$ und für $n < N_j$: \begin{eqnarray*} D_n*K_{N_j} &=&K_{N_j}*D_n =\s_{N_j}(D_n)\\ &=&(1+N_j)^{-1}(S_0(D_n)+\cdots+S_n(D_n) +S_{n+1}(D_n)+\cdots+S_{N_j}(D_n))\\ &=&(1+N_j)^{-1}(D_0+\cdots+D_n+(N_j-n)D_n)\\ &=&\frac{n+1}{1+N_j}K_n+\frac{N_j-n}{1+N_j}D_n \end{eqnarray*} und damit: $$ \sum_{j:n < N_j}2^{-j}D_n*K_{N_j} =\sum_{j:n < N_j}2^{-j}\frac{n+1}{1+N_j}K_n+2^{-j}\frac{N_j-n}{1+N_j}D_n $$ Der erste Summand ist i.W. $2^{-J_n}K_n$ und der zweite $2^{-J_n}D_n$, wobei $J_n=\inf\{j:N_j>n\}$; da $\norm{2^{-J_n}D_n}_1\sim 2^{-J_n}\log n$ folgt für $N_j\sim\exp(\exp(j))$: $J_n\sim\log\log n$ und damit $2^{-J_n}\log n\sim 1$.
Sei $\vp:\R_0^+\rar\R_0^+$ eine konvexe, monoton fallende Funktion mit $\lim_{x\to\infty}\vp(x)=0$. Dann gilt: $\lim_{x\to\infty}x\vp^\prime(x)=0$ und $\int_0^\infty x\vp^\dprime(x)\,dx=\vp(0)$.
Da $\vp$ konvex ist, gilt für alle $x,y\geq0$: $\vp(y)\geq\vp(x)+\vp^\prime(x)(y-x)$. Setze $y=x/2$, dann folgt: $$ -\vp^\prime(x)x\leq2(\vp(x/2)-\vp(x))~. $$ 2. Dies folgt mittels partieller Integration.
Sei $a_n$ eine gerade Folge positiver reeller Zahlen, konvex auf $\N_0$ und in $\infty$ verschwindend. Dann gilt: 1. Die Partialsummen von $\sum a_ne^{int}$ ist in $L_1(\TT)$ beschränkt, falls $a_n\log n=\Oh(1)$. 2. $\sum a_ne^{int}$ konvergiert in $L_1(\TT)$, falls $a_n\log n=\oh(1)$.
Sei $f(t)\colon=\sum_{n\geq1} n(a_{n-1}+a_{n+1}-2a_n)K_{n-1}(t)$, dann gilt (vgl. Beweis zu Satz \ref{nonks1}): $f\in L_1(\TT)$, $f\geq0$ und $\wh f(n)=a_n$. \begin{eqnarray*} S_N(f) &=&D_N*f =\sum_{n\leq N+1}n(a_{n-1}+a_{n+1}-2a_n)K_{n-1}\\ &&+\sum_{n>N+1}n(a_{n-1}+a_{n+1}-2a_n)D_N*K_{n-1} \end{eqnarray*} Die $L_1$-Norm der ersten Summe ist gleich $$ \sum_{n\leq N+1}n(a_{n-1}+a_{n+1}-2a_n) =a_0-a_N-N(a_N-a_{N+1}) $$ und dies konvergiert mit $N\to\infty$ gegen $0$. Die $L_1$-Norm der zweiten Summe ist beschränkt durch $$ \sum_{n>N+1}n(a_{n-1}+a_{n+1}-2a_n)\norm{D_N}_1 \leq Ka_N\log N $$ Falls also $a_n\log n=\Oh(1)$, dann sind die Partialsummen beschränkt und falls $a_n\log n=\oh(1)$, dann konvergieren die Partialsummen.
Sei $0 < a\leq\pi$ und $\D_a(t)=(1-|t|/a)\vee 0$. Dann liegt $\D_a$ in $A(\TT)$ und es gilt $\norm{\D_a}_{A(\TT)}=1$.
Da $\D_a$ symmetrisch ist, gilt $$ \D_a(t)=\tfrac12a_0+\sum_{n\geq1}a_n\cos(nt) $$ mit $a_0=\frac1\pi\int\D_a(t)\,dt=a/\pi$ und für $n\geq1$: $$ a_n=\frac2\pi\int_0^a(1-t/a)\cos(nt)\,dt =\frac a\pi\Big(\frac{\sin(an/2)}{an/2}\Big)^2 $$ Die Reihe $\sum a_n$ ist also absolut konvergent. Da $\D_a(0)=1$, folgt: $\sum_{n\geq0} a_n=\D_a(0)=1$.
Seien $f,g\in L_2(\TT)$, dann gilt: $f*g\in A(\TT)$.
Es gilt: $$ \sum|\wh{f*g}(n)| =\sum|\wh f(n)||\wh g(n)| \leq(\sum|\wh f(n)|^2)^{1/2}(\sum|\wh g(n)|^2)^{1/2} =\norm f_2\norm g_2 $$
Der Sobolevraum $H^s(\TT)$ ist für alle $s > 1/2$ eine Algebra, i.e. mit $f$ und $g$ ist auch $fg$ in $H^s(\TT)$.
Sei für $n\in\Z$: $h(n)\colon=(1+|n|^2)^{1/2}$, dann gilt für alle $s>1/2$ mit einer geeigneten Konstante $C(s)$: $$ \forall m,n\in\Z:\quad \sum_{k\in\Z}h(k-n)^{-2s}h(m-k)^{-2s} \leq C(s)h(m-n)^{-2s}~. $$ Mit $F(n)\colon=|\wh f(n)|h(n)^s$ und $G(n)\colon=|\wh g(n)|h(n)^s$ folgt nach der Cauchy-Schwarz Ungleichung: \begin{eqnarray*} \norm{fg}_{H^s}^2 &=&\sum_m\Big(\sum_k\wh f(k)h(k)^s\wh g(m-k)h(m-k)^s h(k)^{-s}h(m-k)^{-s}\Big)^2h(m)^{2s}\\ &\leq&\sum_m\Big(\sum_k F(k)^2G(m-k)^2\Big) \Big(\sum_k\Big(\frac{h(m)}{h(k)h(m-k)}\Big)^{2s}\Big)\\ &\leq&C(s)\norm f_{H^s}^2\norm g_{H^s}^2~. \end{eqnarray*}
Der Sobolevraum $H^s(\TT^d)$ ist für alle $s>d/2$ eine Algebra, i.e. mit $f$ und $g$ ist auch $fg$ in $H^s(\TT^d)$.
Für alle $t > 0$ ist die kanonische Einbettung $H^{s+t}(\TT)\hrar H^s(\TT)$ kompakt.
Sei für $t\in\R$ und $\theta\in\TT$: $$ J^t(f)(\theta)\colon=\sum_{m\in\Z}\wh f(m)(1+m^2)^{t/2}e^{im\theta} $$ Dann ist nach Definition der Norm auf $H^s(\TT)$ die Abbildung $J^t:H^{s+t}(\TT)\rar H^s(\TT)$ ein isometrischer Isomorphismus. Andererseits ist für alle $t>0$ und alle $s\in\R$: $J^{-t}:H^s(\TT)\rar H^s(\TT)$ als Norm-Limes von Operatoren endlichen Ranges kompakt und folglich ist die Komposition $J^{-t}J^t:H^{s+t}(\TT)\rar H^s(\TT)$ kompakt.
Für alle $t>0$ ist die kanonische Einbettung $H^{s+t}(\TT^d)\hrar H^s(\TT^d)$ kompakt.
Sei $f\in C^\infty(\TT^d)$ und für $k=0,\ldots,d$: $$ R_kf(\theta_1,\ldots,\theta_{d-k}) \colon=f(\theta_1,\ldots,\theta_{d-k},1,\ldots,1)~. $$ Dann ist für $s>k/2$: $R_k:H^s(\TT^d)\rar H^{s-k/2}(\TT^{d-k})$ stetig und surjektiv.
Seien $y=(y_1,\ldots,y_{d-k})\in\R^{d-k}$, $y_{d-k+1}=\cdots=y_d=0$, $\theta_j=e^{iy_j}$ und $\theta=(\theta_1,\ldots\theta_d)$, $u=v+w$, $v\in\Z^{d-k}$ orthogonal zu $w\in\Z^k$. Dann gilt: $$ f(\theta)=\sum_{w\in\Z^k,v\in\Z^{d-k}}\wh f(v+w)e^{i\la v,y\ra} =\sum_{\Z^{d-k}}\sum_{\Z^k}\wh f(v+w)\,e^{i\la v,y\ra}~. $$ Somit ist $\wh{R_kf}(v)=\sum_{\Z^k}\wh f(v+w)$ und mit $r\colon=s-k/2$ folgt nach der Cauchy Schwarz Ungleichung: \begin{eqnarray*} \norm{R_kf}_{H^r}^2 &=&\sum_{v\in\Z^{d-k}}\Big|\sum_{w\in\Z^k}\wh f(v+w)\Big|^2(1+\norm v^2)^r\\ &=&\sum_{v\in\Z^{d-k}}\Big|\sum_{w\in\Z^k}\wh f(v+w) \left(\tfrac{1+\norm{v+w}^2}{1+\norm{v+w}^2}\right)^{s/2} \Big|^2(1+\norm v^2)^r\\ &\leq&\sum_{v\in\Z^{d-k}} \Big(\sum_{w\in\Z^k}|\wh f(v+w)|^2(1+\norm{v+w}^2)^s\Big)\\ &&\qquad\times\Big(\sum_{w\in\Z^k}(1+\norm{v+w}^2)^{-s}\Big) (1+\norm v^2)^r~. \end{eqnarray*} Nun ist $$ \sum_{w\in\Z^k}(1+\norm v^2+\norm w^2)^{-s} \leq c(s,d,k)(1+\norm v^2)^{-r}, $$ also erhalten wir: $$ \norm{R_kf}_{H^r}^2 \leq c(s,d,k)\sum_{v\in\Z^{d-k}}\Big(\sum_{w\in\Z^k} \wh f(v+w)^2(1+\norm{v+w}^2)^s\Big) =c(s,d,k)\norm f_{H^s}^2~. $$ Sei $g\in H^{s-k/2}(\TT^{d-k})$, dann ist durch $$ \forall w\in\Z^k,\forall v\in\Z^{d-k}:\qquad \wh f(v+w)\colon=\wh g(v)(1+\norm v^2)^{s-1/2}(1+\norm{v+w}^2)^{-s} $$ ein Element $f$ in $H^s(\TT^d)$ definiert und es gilt mit einer Konstante $c\neq0$: $R_kf=cg$
Konstruktion von Rudin und Shapiro: eine Funktion in $\lip_{1/2}(\TT)$, deren Fourierreihe nicht absolut konvergiert. Definiere trigonometrische Polynome $P_m$ und $Q_m$ induktiv durch $P_0=Q_0=1$ und $$ P_{m+1}(t)=P_m(t)+e^{2^mit}Q_m(t)\qquad Q_{m+1}(t)=P_m(t)-e^{2^mit}Q_m(t) $$ 1. Zeigen Sie: $|P_{m+1}|^2+|Q_{m+1}|^2=2(|P_m|^2+|Q_m|^2)$ und folgern Sie: $$ |P_m|^2+|Q_m|^2=2^{m+1} \quad\mbox{und}\quad \norm{P_m}_\infty,\norm{Q_m}_\infty\leq2^{(m+1)/2}~. $$ 2. Es gibt eine Folge von Vorzeichen $\e_n=\pm1$, so daß $$ P_m(t)=\sum_{n=0}^{2^m-1}\e_ne^{int} $$ 3. Sei $f_m\colon=P_m-P_{m-1}$ und $f\colon=\sum 2^{-m}f_m$, dann liegt $f$ in $\lip_{1/2}(\TT)$ aber nicht in $A(\TT)$.
1. Es gilt \begin{eqnarray*} |P_{m+1}|^2 &=&(P_m(t)+e^{2^mit}Q_m(t))(\bar P_m(t)+e^{-2^mit}\bar Q_m(t))\\ &=&|P_m|^2+|Q_m|^2+2\Re(e^{2^mit}Q_m(t)\bar P_m(t)) \end{eqnarray*} sowie \begin{eqnarray*} |Q_{m+1}|^2 &=&(P_m(t)-e^{2^mit}Q_m(t))(\bar P_m(t)-e^{-2^mit}\bar Q_m(t))\\ &=&|P_m|^2+|Q_m|^2-2\Re(e^{2^mit}Q_m(t)\bar P_m(t)) \end{eqnarray*} Also: $|P_{m+1}|^2+|Q_{m+1}|^2=2(|P_m|^2+|Q_m|^2)$; mittels Induktion folgt: $|P_m|^2+|Q_m|^2=2^{m+1}$ und daraus: $|P_m|^2\leq|P_m|^2+|Q_m|^2=2^{m+1}$. 2. Dies folgt wiederum mittels Induktion; es gilt z.B.: $P_1(t)=1+e^{it}$, $Q_1(t)=1-e^{it}$, $P_2(t)=1+e^{it}+e^{2it}-e^{3it}$, $Q_2(t)=1+e^{it}-e^{2it}+e^{3it}$. 3. Nach Konstruktion folgt: $$ f_m(t)=e^{2^{m-1}it}Q_{m-1}(t) =\sum_{n=2^{m-1}}^{2^m-1}\e_ne^{int} $$ Da die Spektren der Folge $f_m$ paarweise disjunkt sind, folgt: $$ \sum_n|\wh f(n)| =\sum_m2^{-m}\norm{f_m}_{A(\TT)} =\infty \quad\mbox{d.h.}\quad f\notin A(\TT)~. $$ Sei zu $t\in\TT$, $k\in\N$ und $h>0$: $$ I\colon=\sum_{m=1}^k 2^{-m}(f_m(t+h)-f_m(t)) \quad\mbox{und}\quad II\colon=\sum_{m>k} 2^{-m}(f_m(t+h)-f_m(t)) $$ Dann gilt nach 1.: $$ |II|\leq\sum_{m>k}2^{-m}2\norm{Q_{m-1}}_\infty =2\sum_{m>k}2^{-m/2} \leq c_12^{-(k+1)/2} $$ $f_m(t+h)-f_m(t)$ ist ein trigonometrische Polynom in $t$ des Grades $2^m-1$, also folgt nach dem Mittelwertsatz, der Bernstein Ungleichung sowie 1.: \begin{eqnarray*} |f_m(t+h)-f_m(t)|\leq h\tnorm{f_m^\prime}_\infty &=&h\tnorm{Q_{m-1}^\prime}_\infty \leq2(2^m-1)\tnorm{Q_{m-1}}_\infty\\ &\leq&2(2^m-1)2^{m/2}~. \end{eqnarray*} Somit erhalten wir: $$ |I|\leq\sum_{m=1}^k 2^{-m}2(2^m-1)2^{m/2}h \leq2^{3/2}\sum_{m=0}^{k-1} 2^{m/2}h \leq c_22^{k/2}h $$ Wählen wir zu $h>0$ $k\colon=\sup\{j:2^jh\leq1\}$, i.e. $2^{-(k+1)}
Sei $\vp(t)\colon=(t-1)^+$, dann ist $\Phi(t)=\log^+t$ die Stammfunktion von $\vp^\prime(t)/t$. 2. Zeigen Sie, daß für $a,b\geq0$ gilt: $a\log b\leq a\log^+a+b/e$. 3. Ist $|f|\log^+|f|$ integrierbar, so gilt: $$ \int_{\TT} f^*\,d\l \leq\frac{e}{2\pi(e-1)}\Big(1+\int_{\TT} |f|\log^+|f|\,d\l\Big)~. $$
3. Es gilt nach 2. mit $\mu\colon=\l/2\pi$: $$ \int(f^{*}-1)^+\,d\mu \leq\int\log^+(f^*)|f|\,d\mu \leq\int|f|\log^+|f|\,d\l+e^{-1}\int f^*\,d\mu $$ Schließlich ist $f^*\geq|f|$ und damit $\mu(f^*\leq1)\leq\mu(|f|\leq1)$, also: \begin{eqnarray*} \int f^*\,d\l &=&\int_{f^* > 1}f^{*}\,d\mu -\mu(f^* > 1)-\mu(f^*\leq1)+1 +\int_{f^*\leq 1}f^{*}\,d\mu\\ &=&\int(f^{*}-1)^+\,d\mu-\mu(f^*\leq1)+\int_{f^*\leq 1}f^{*}\,d\mu+1\\ &\leq&\int(f^{*}-1)^+\,d\mu+1 \leq\int|f|\log^+|f|\,d\l+e^{-1}\int f^*\,d\mu+1 \end{eqnarray*}
Sei $g:\R_0^+\rar\R$ stetig und $$ U(g)=\{x\in\R^+:\,\exists y > x \quad g(y) > g(x)\}~. $$ Dann ist $U(g)$ die abzählbare Vereinigung paarweise disjunkter offener Intervalle $I_n=(a_n,b_n)$. Falls $a_n=0$, dann gilt: $g(a_n)\leq g(b_n)$ und falls $a_n > 0$, dann gilt: $g(a_n)=g(b_n)$.
Sei $f\in L_1(\TT)$ und $$ f^*(\theta)\colon=\sup_{t > 0}\frac1t\int_{\theta}^{\theta+t}|f(u)|\,du~. $$ Zeigen Sie, daß füralle $f\in L_1(\mu)$ und alle $s > 0$ gilt: $$ s\l(f^* > s)\leq\int_{[f^* > s]}|f(u)|\,du~. $$
Sei $g:\R_0^+\rar\R$ rechtsstetig mit linksseitigen Limiten $g(x-)$ und $$ U(g)=\{x\in\R^+:\,\exists y > x \quad g(y) > g(x)\}~. $$ Dann ist $U(g)$ die Vereinigung von höchstens abzählbar vielen paarweise disjunkten Intervallen der Form $(a,b)$ oder $[a,b)$. Zeigen Sie: $g(a)\leq g(b-)$.
← Homogene Räume → Hilbert-Transformation
<Home>
Last modified: Tue Oct 31 12:44:04 CET 2023