Mean Convergence
A Tauberian result
In the sequel let $P_t:E\rar E$, $t\in\R_0^+$ (or $t\in\N_0$) be any continuous contraction semigroup on a Banach space $E$ with generator $L$ - in the discrete case $L$ denotes the difference operator $P-1$. We are looking for conditions, which guarantee the convergence of the arithmetic mean $$ A_tx\colon=\frac1t\int_0^t P_sx\,ds \quad\mbox{or}\quad A_nx\colon=\frac1n\sum_{j=0}^{n-1} P^jx~. $$ as $t$ (or $n$) converges to $\infty$. We will only elaborate on the continuous case, the discrete case is very similar - just keep in mind that in the discrete case the generator has to be replaced with the difference operator! We start with a few easy but essential situations: 1. if $x\in\ker L$, then $P_tx=x$ and thus $A_tx=x$. 2. If $x\in\im L$, then $x=Ly$ and by proposition: $$ A_tx =\frac1t\int_0^tP_sLy\,ds =\frac{P_ty-y}t $$ and therefore $A_tx$ converges to $0$.Now the set $F$ of all $x\in E$ for which $A_tx$ converges (as $t\to\infty$) is closed: if $x_n\in F$ converges to $x\in E$, then the sequence of continuous functions $f_n(t)\colon=t\mapsto A_tx_n$ converges in $C_b([0,\infty],E)$ to $f(t)=A_tx$ and thus $f$ is continuous at $t=\infty$. Hence we've found a sufficient condition: if $\ker L+\im L$ is dense then $A_tx$ converges for all $x\in E$. The Mean Ergodic Theorem states that this is in fact an equivalent condition. $\proof$ We notice that $\int f_b(t)\,dt=\int f_1(t)\,dt$ and thus: $$ \lim_{a\to\infty}a^{-1}\int g(t)f_b(t/a)\,dt =\lim_{a\to\infty}(ab)^{-1}\int g(t)f_1(t/ab)\,dt =x\int_0^\infty f_1(t)\,dt =x\int_0^\infty f_b(t)\,dt~. $$ Since the set $\{f_b: b > 0\}$ spans a dense subspace $D$ of $L_1(\R^+)$, we can find for every $\e > 0$ and every $f\in L_1(\R^+)$ a function $h\in D$ satisfying: $\Vert f-h\Vert_1 < \e$. For this function $h\in D$ we know that for all $a\geq a_0$: $$ \Big|\int g(t)a^{-1}h(t/a)-x\int h(t)\,dt\Big| < \e $$ Hence we conclude that for all $a\geq a_0$: \begin{eqnarray*} \Big|\int g(t)a^{-1}f(t/a)\,dt-x\int f(t)\,dt\Big| &\leq&\Big|\int g(t)a^{-1}(f(t/a)-h(t/a))\,dt\Big|\\ &&+\Big|\int g(t)a^{-1}h(t/a)\,dt-x\int h(t)\,dt\Big|+\Big|x\int f(t)-h(t)\,dt\Big|\\ &\leq&\Vert g\Vert_\infty\Vert f-h\Vert_1+\e+\Vert f-h\Vert_1\Vert x\Vert \end{eqnarray*} $\eofproof$ Functions $f_1$ satisfying the requirements of the lemma are $f_1(t)=I_{(0,1]}(t)$ and $f_1(t)=e^{-t}$. In the first case all indicators $I_{(a,b]}$ are in $D$ and thus the subspace $D$ is obviously dense in $L_1(\R^+)$. However, the second case is not that obvious! If $D$ is not dense then by Hahn-Banach there is some $h\in L_\infty(\R^+)$ such that for all $s > 0$: $\int h(t)e^{-st}\,dt=0$. The function $$ F(z)\colon=\int_0^\infty h(t)e^{-zt}\,dt $$ is analytic on $\Re z > 0$ and vanishes on $\R^+$; by the Identity Theorem for analytic functions it must vanish identically. Hence the Fourier transform of the integrable function $h(t)e^{-t}I_{\R^+}(t)$ vanishes, i.e. $h=0$.
The mapping $L_1(\R^+)\rar L_1(\R)$, $f\mapsto F:x\mapsto f(e^x)e^x$ is an isometry onto $L_1(\R)$ which maps $f_a$ onto $x\mapsto f_a(e^x/a)e^x/a$; putting $a=e^y$ it follows that $f_a$ is mapped onto $F_y(x)=f(e^{x-y})e^{x-y}=L_yF(x)$. Hence the image of the subspace generated by $f_a$, $a > 0$ is the space generated by all translations of $F$. By Wiener's theorem the image is dense iff the Fourier transform $\wh F$ has no real zero, i.e. iff $$ \forall y\in\R:\quad 0\neq\int_\R f(e^x)e^{x-ixy}\,dx =\int_0^\infty f(t)t^{-iy}\,dt~. $$ The last integral is called the Mellin-transform of $f$. Consulting this result the function $f_1(t)=e^{-t}$ satisfies the requirements if for all $y\in\R$: $$ 0\neq\int_0^\infty t^{-iy}e^{-t}\,dt $$ but this is just $\G(1-iy)$ and the $\G$-function doesn't vanish at any point!
Suppose $\Re w > 1$. Check if $f_1(t)=(\pi(1+t^w))^{-1}$ satisfies the assumptions in lemma. Hint: use
$$
\frac1{\pi}\int_0^\infty\frac{t^{-iy}}{1+t^w}\,dt
=\frac{1}{w\sin(\frac{1-iy}{w}\pi)}~.
$$
The mean ergodic theorem
Beside the afore discussed Tauberian result we need two additional results: 1. the generator $L$ is closed. 2. Every closed convex subset of a Banach space is weakly closed - that`s a consequence of the Hahn-Banach Theorem. These are the essential ingredients in the proof of the Mean Ergodic Theorem: $\proof$ By Lemma (for $f_1=I_{(0,1]}$, $a=\l$ and $f_1(t)=e^{-t}$, $a=1/\l$ respectively) each of the first two conditions implies: \begin{equation}\label{haeq1}\tag{COM1} \forall f\in L_1(\R^+):\quad \lim_{\l\to0}\l\int_0^\infty f(\l t)P_tx\,dt =\Big(\int_0^\infty f(t)\,dt\Big)Qx~. \end{equation} Let us define a subspace $F$ by $$ F\colon= \Big\{x\in E:\lim_{a\to\infty}\frac1a\int_0^a P_tx\,dt\mbox{ exists}\Big\}~. $$ We already know that $F$ is closed.1.$\Rar$3. and 2.$\Rar$4. are obvious!
2.$\Rar$5.: We clearly have for all $x\in E$: $\norm{Qx}\leq\Vert x\Vert$; moreover $Q$ and $P_t$ commute. Put for $\l > 0$: $$ Q_\l x\colon=\l\int_0^\infty e^{-\l s}P_sx\,ds $$ then Fubini and the substitution $(u,v)=(s+t,s)$ yield (cf. also exam): \begin{eqnarray*} Q_\l^2 x &=&\l\int_0^\infty e^{-\l s}P_sQx\,ds\\ &=&\l^2\int_0^\infty\int_0^\infty e^{-\l(s+t)}P_{s+t}x\,ds\,dt\\ &=&\l^2\int_0^\infty\int_0^u e^{-\l u}P_ux\,dv\,du =\l\int_0^\infty(\l u)e^{-\l u}P_ux\,du~. \end{eqnarray*} Since $\Vert Q_\l\Vert\leq1$ and for all $x\in E$: $\lim_{\l\to0}Q_\l x=Qx$, it follows that $\lim_{\l\to0}Q_\l^2 x=Q^2x$. By \eqref{haeq1} we get for the function $f(u)=ue^{-u}$: $$ Q^2x =\lim_{\l\to0}Q_\l^2x =\lim_{\l\to0}\l\int_0^\infty(\l u)e^{-\l u}P_ux\,du =\Big(\int_0^\infty f(t)\,dt\Big)Qx =Qx~. $$ Hence $Q$ is a projection.
Claim: $\im Q=\ker L$: For $x\in\im Q$ put $x_\l\colon=\l(\l-L)^{-1}x\in\dom L$. Then by 2.: $\lim_{\l\to0}x_\l=x$. In addition we have $$ \lim_{\l\to0}Lx_\l =\lim_{\l\to0}\l L(\l-L)^{-1}x =\lim_{\l\to0}\l(L-\l+\l)(\l-L)^{-1}x =\lim_{\l\to0}(\l x_\l-\l x)=0 $$ and since $L$ is close: $x\in\dom L$ and $Lx=0$. Conversely, assume $x\in\dom L$ and $Lx=0$. Then for all $t\geq 0$: $P_tx=x$, which in turn implies $Qx=x$.
Claim: $\im L$ is dense in $\ker Q$: Suppose $x\in\im L$ i.e. $x=Ly$. Then, as we've seen before: $$ Qx =QLy =\lim_{a\to\infty}\frac1a\int_0^a P_tLy\,dt =\lim_{a\to\infty}\frac1a(P_ay-y) =0~. $$ Hence $x\in\ker Q$. Conversely, if $x\in\ker Q$, then $x_\l\colon=-(\l-L)^{-1}x$ is in $\dom L$ and $$ \lim_{\l\to0}(x-Lx_\l) =\lim_{\l\to0}(x+L(\l-L)^{-1}x) =\lim_{\l\to0}\l(\l-L)^{-1}x =Qx =0~. $$ 5.$\Rar$1. This implication has been proved at the beginning of this chapter!
3.$\Rar$1.: We will show that $D\sbe F$. $F$ is also weakly closed and since for all $x\in\im L$: $A_tx\to0$, we have for all $x\in\cl{\im L}$: $A_tx\to0$. For any $x\in D$ we can find a sub-sequence $x_n=A_{t_n}x$ such that $x_n$ converges weakly to $y$ (by the Eberlein-Smulian Theorem). By proposition the function $t\mapsto tA_tx$ is $\dom L$ valued and $L(tA_tx)=P_tx-x$. Hence $Lx_n$ converges to $0$ and since $L$ is also weakly closed: $y\in\dom L$ and $Ly=0$, i.e. $P_ty=y$. It follows that $$ x_n=A_{t_n}x=A_{t_n}(x-y)+A_{t_n}y=A_{t_n}(x-y)+y $$ and thus we are left to prove that $A_{t_n}(x-y)$ converges to $0$. This holds if $x-y\in\cl{\im L}$. So suppose $x-y\notin\cl{\im L}$; by Hahn Banach we can find a unit functional $x^*\in E^*$, such that $x^*|\cl{\im L=0}$ but $x^*(x-y)\neq0$. Again by proposition: $P_tx-x=L(tA_tx)$ and therefore for all $t$: $x^*(P_tx)=x^*(x)$, which implies for all $t$: $x^*(A_tx)=x^*(x)$. On the other hand $x^*(A_{t_n})$ converges to $x^*(y)$, i.e. $x^*(x-y)=0$, which is a contradiction.
4.$\Rar$2.: Again we will show that $D\sbe F$. For every $x\in D$ there is a null sequence $\l_n\in\R^+$, such that $y_n\colon=\l_n(\l_n-L)^{-1}x\in\dom L$ converges weakly to $y$; since $Ly_n=\l_ny_n-\l_nx$, we infer that $Ly_n$ converges weakly to $0$. Now $L$ is closed and by Hahn-Banach it's weakly closed. Hence $y\in\dom L$ and $Ly=0$. We have to prove that $x\in F$: Now $x=\l_n^{-1}(\l_n-L)y_n=y_n-\l_n^{-1}Ly_n$, so let us put $$ x_n\colon=y-\l_n^{-1}Ly_n, $$ then $x_n\in\ker L+\im L\sbe F$ and $x_n-x=y-y_n$ converges weakly to $0$. Since $F$ is weakly closed, it follows that: $x\in F$. Hence $D\sbe F$ and therefore: $F=E$.
6.$\Rar$1.: Suppose $x\in\im L_a$, then $x=P_ay-y$ and $$ \lim_{t\to\infty}A_tx =\lim_{t\to\infty}\frac1t\int_0^t P_{s+a}y-P_sy\,ds =\lim_{t\to\infty}\frac1t\Big(\int_t^{t+a}P_sy\,ds-\int_0^a P_sy\,dx\Big) =0 $$ and therefore $F_0\sbe F$. As $F_0$ is dense and $F$ is closed, we infer that $F=E$.
5.$\Rar$6.: By definition of $L$ we have for $x\in\dom L$: $$ Lx =\lim_{a\dar0}\frac{P_a x-x}{a} =\lim_{a\dar0}a^{-1}L_a x \quad\mbox{i.e.}\quad \cl{\bigcup_{a > 0}\im L_a}\spe\im L $$ $\eofproof$
If $P:E\rar E$ is a linear contraction, then (suggested solution)
$$
\norm{e^{n(P-1)}x-P^nx}\leq\sqrt n\norm{(P-1)x}
$$
If $P_t=e^{tL}:E\rar E$ satisfies one of the conditions in the Mean Ergodic Theorem, then for all $x\in\ker Q$: $\lim_{\l\dar0}LU_\l x=-x$.
For e.g. the heat semigroup $P_t=e^{-t\D}$ on $L_2(\R^d)$ we have by exam: $\ker\D=\{0\}$ and thus $\im\D$ is dense and $A_tf$ converges in $L_2(\R^d)$ to $0$. Since $P_t$ is ultracontractive $P_tf$ converges to $0$ in $L_\infty(\R^d)$ for all $f\in L_p(\R^d)$, $p < \infty$, as $t\uar\infty$. For the heat semigroup $P_t=e^{-t\D}$ on $L_2(\TT^d)$ the kernel of $\D$ is the one dimensional subspace of constant functions and $\cl{\im\D}$ is the orthogonal complement of the constant functions. The same holds for any diffusion semigroup $P_t=e^{-tH}$ on a Riemannian manifold satisfying the assumptions of proposition. The Ornstein-Uhlenbeck semigroup (cf. proposition) is a typical example for this type of semigroup. Also the kernel of the generator of the Poisson semigroup is the space of constant functions; however in this case it's pretty obvious from the formula given in proposition that $P_tf$ converges to $\int f\,d\s$ as $t\uar\infty$.
Suppose $E$ is reflexive or the set $\{P_tx:\,t > 0\}$ is weakly relatively compact for all $x$ in a weakly dense subset $D$. Then all of the conditions in the Mean Ergodic Theorem hold.
$\proof$
Since $\{\l(\l-L)^{-1}x:0 < \l\leq1\}$ is bounded anyway, it's weakly relatively compact if $E$ is reflexive. If $\{P_tx:\,t > 0\}$ is contained in a weakly compact subset $C$, then for all $\l > 0$:
$$
\l(\l-L)^{-1}x
=\int_0^\infty\l e^{-\l t}P_tx\,dt
\in\cl{\convex{C}}
$$
But by the Krein-Smulian Theorem the closed convex hull $\cl{\convex{C}}$ of $C$ is again a weakly compact subset.
$\eofproof$
Index
Diffusions on compact manifolds have a compact resolvent in e.g. $L_2(\mu)$. It turns out that for semigroups with compact resolvent the operators $A_t$ converge in the operator norm:
If $\{P_tx:\,t > 0\}$ is relatively compact or weakly relatively compact, then all of the conditions in the Mean Ergodic Theorem hold. If in addition $(\l-L)^{-1}$ is compact for some $\l > 0$, then $\ker L$ is finite dimensional and $\im L$ is closed and thus $E=\ker L\oplus\im L$. It follows that the index $\ind(L)$ of $A$, which is defined as the difference $\dim\ker L-\dim E/\im L$, vanishes. Cf. exam.
Suppose $\im L$ is closed. Use the uniform boundedness principle to show that the family of operators $tA_t$, $t > 0$ is uniformly bounded on $\im L$, i.e. there is some constant $C < \infty$ such that for all $x\in\im L$:
$$
\sup\{\norm{tA_tx}: t > 0\}\leq C\Vert x\Vert~.
$$
2. If moreover $E=\ker L\oplus\im L$, then $\lim_{t\to\infty}\norm{A_t-Q}=0$ and $\lim_{\l\to0}\norm{\l(\l-L)^{-1}-Q}=0$. Suggested solution.
If $\l\neq0$ is an eigenvalue of $AB$, then $\l$ is also an eigenvalue of $BA$ and $B$ is an algebraic isomorphism from $\ker(AB-\l)$ onto $\ker(BA-\l)$ with inverse $\l^{-1}A$. Hence for all $\l\neq0$: $\dim\ker(AB-\l)=\dim\ker(BA-\l)$. Suggested solution
Now assume that $E$ is a Hilbert space and we have an orthogonal decomposition
$$
E=\ker(AB)\oplus\bigoplus_{n\in\N}\ker(AB-\l_n),
$$
where $0 < \Re\l_1 < \Re\l_2 < \cdots$ and $\dim\ker(AB-\l_n) < \infty$. It follows that both $-AB$ and $-BA$ generate continuous contraction semigroups. Denoting by $P_n$ the orthogonal projection onto $\ker(AB-\l_n)$ we infer that for all $x\in E$:
$$
\lim_{t\to\infty}\Vert e^{-tAB}x-P_{\ker(AB)}x\Vert^2
=\lim_{t\to\infty}\sum_{n=1}^\infty e^{-2\l_nt}\Vert P_nx\Vert^2=0
\quad\mbox{and}\quad
\lim_{t\to\infty}\Vert e^{-tBA}x-P_{\ker(BA)}x\Vert^2=0~.
$$
Finally if $\ker(AB)$ and $\ker(BA)$ are of finite dimension and $e^{-tAB}$ is a trace class operator, then for all $t > 0$:
$$
\tr e^{-tAB}=\dim\ker(AB)+\sum e^{-\l_nt}\dim\ker(AB-\l_n)
$$
Hence the function $t\mapsto\tr e^{-tAB}-\tr e^{-tBA}$ is constant and this constant equals $\dim\ker(AB)-\dim\ker(BA)$. In particular for $B=A^*$ this constant equals
$$
\dim\ker(AA^*)-\dim\ker(A^*A)=\dim\ker(A^*)-\dim\ker(A)=-\ind(A)~.
$$
Sufficient conditions for mean convergence
In corollary we formulated a sufficient condition for mean convergence; here are a few more!
Suppose $P_t$ is a positive continuous contraction semigroup on $L_1(\mu)$, such that there is a strictly positive function $f_1\in L_1(\mu)$ satisfying $Lf_1=0$. Then the conditions in the Mean Ergodic Theorem hold for $E=L_1(\mu)$.
$\proof$
For $a > 0$ put $C_a\colon=\{f:|f|\leq af_1\}$. Since $P_t$ is positive, it follows that for all $f\in C_a$ and all $\l > 0$:
$$
\l\int_0^\infty P_tfe^{-\l t}\,dt\in C_a~.
$$
Now $C_a$ is weakly compact (cf. Dunford-Pettis Theorem) and $\bigcup_{a > 0}C_a$ is dense: for any $f\in L_1(\mu)$ put $f_n\colon=f\wedge nf_1\vee-nf_1$, then $f_n\in C_n$ and $f_n\to f$ in $L_1(\mu)$ by dominated convergence.
$\eofproof$
The following is of greater importance to us:
Let $\mu$ be a probability measure and let $P_t$ be a continuous contraction semigroup on $L_1(\mu)$, such that $\norm{P_t:L_\infty(\mu)\rar L_\infty(\mu)}\leq1$. Then for all $1\leq p < \infty$ the conditions in the Mean Ergodic Theorem hold for $E=L_p(\mu)$.
$\proof$
By the Riesz-Thorin Interpolation Theorem: $\norm{P_t:L_p(\mu)\rar L_p(\mu)}\leq1$. For $f\in L_1(\mu)\cap L_\infty(\mu)$ we have:
$$
\norm{P_tf-f}_p
\leq\norm{P_tf-f}_1^{1/p}\norm{P_tf-f}_\infty^{1-1/p}~.
$$
Since $L_1(\mu)\cap L_\infty(\mu)$ is dense in $L_p(\mu)$ we infer by lemma that $P_t$ is a continuous contraction semigroup on $L_p(\mu)$. For $p > 1$ the space $L_p(\mu)$ is reflexive and the assertion follows immediately from the Mean Ergodic Theorem. As for $p=1$ we take any $f\in L_\infty(\mu)$ and claim that the set
$$
\{\l(\l-L)^{-1}f:0 < \l\leq1\}
$$
is bounded in $L_\infty(\mu)$: Indeed, for all $g\in L_1(\mu)$ and all $\l > 0$:
$$
\Big|\int g\l(\l-L)^{-1}f\,d\mu\Big|
=\l\Big|\int_0^\infty e^{-\l s}\int gP_sf\,d\mu\Big|
\leq\norm g_1\norm f_\infty
$$
and thus: $\norm{\l(\l-L)^{-1}f}_\infty\leq\norm f_\infty$. Now the Banach-Alaoglu Theorem implies that $\{\l(\l-L)^{-1}f:0 < \l\leq1\}$ is relatively weakly * compact in $L_\infty(\mu)$ for all $f\in L_\infty(\mu)$. Finally the weak * topology on $L_\infty(\mu)$ is stronger than the weak topology on $L_\infty(\mu)$ inherited from $L_1(\mu)$ and we are done by the Mean Ergodic Theorem.
$\eofproof$
Prove that proposition also holds for $p > 1$ for arbitrary measures $\mu$.
Let $\mu$ be a probability measure and let $P_t$ be a continuous contraction semigroup on both $L_1(\mu)$ and $L_2(\mu)$. Then for all $1\leq p\leq2$ the conditions in the Mean Ergodic Theorem hold for $E=L_p(\mu)$.
Identifying the projection
Finally we want to identify the projection $Q$ in case $P_t$ is a positive continuous contraction semigroup on $L_p(\mu)$ and $\mu$ is finite, i.e. $\mu$ is a probability measure. $\proof$ Suppose $x\in\ker Q$, $\Vert x\Vert=1$, $y=Qy$ and $\la x,y\ra=t > 0$. Then: $\norm{-tx+y}^2=\norm y^2-2t+t^2$. Since $Q(-tx+y)=y$, it follows that for small $t$: $\norm Q > 1$. $\eofproof$
Let $\mu$ be a probability measure and $Q$ a positive projection on $L_1(\mu)$ such that $Q(1)=1$. Then $Q$ is the conditional expectation given the $\s$-Algebra $\F^I\colon=\s(f\in L_1(\mu):Qf=f)$.
$\proof$
Put $E\colon=\{f\in L_1(\mu):Qf=f\}$. For $f\in E$ we have $0\leq|f|=|Qf|\leq Q|f|$. Hence if $|f|\neq Q|f|$, then $\norm{f} < \norm{Q|f|}$, which is impossible. Therefore $E$ is a closed sub-lattice of $L_1(\mu)$; it follows that $f^+\in E$ and $nf^+\wedge1\in E$. As $n$ converges to $\infty$ the latter converges in $L_1(\mu)$ to $I_{[f > 0]}$. Thus $E$ is just the space of all $\F^I$-measurable functions and for $A\in\F^I$ and $f\in L_2(\mu)$ we conclude by lemma:
$$
\int_Af\,d\mu
=\int fQ(I_A)\,d\mu
=\int Q(f)I_A\,d\mu~.
$$
Since $Qf$ is $\F^I$-measurable $Qf$ must be the conditional expectation given the $\s$-algebra $\F^I$.
$\eofproof$
$\proof$
Since $P_t$ is conservative we have: $P_t1=1$ and thus $Q1=1$.
$\eofproof$
Moreover, assuming the hypotheses of the previous proposition, $P_t$ is ergodic iff $\F^I$ is trivial, i.e. $A\in\F^I\Rar\mu(A)\in\{0,1\}$ and thus $P_t$ is ergodic on all $L_p(\mu)$, $1\leq p <\infty$ if it is ergodic on some $L_p(\mu)$, $1\leq p < \infty$.If $P_tf=f\circ\theta_t$, then $\F^I$ is the $\s$-algebra of $\theta_t$ invariant sets, i.e. $A\in\F^I$ iff for all $t > 0$: $[\theta_t\in A]=A$ (with respect to $\mu$).
Suppose $P$ is an Markov operator with strictly positive invariant probability measure $\mu$ on a finite set $S$. Then there is a decomposition of $S$ into pairwise disjoint subsets $S_1,S_2,\ldots,S_N$ such that for all $j$: $P|I_{S_j}=I_{S_j}$ and $P:\ell_2(S_j,\mu)\rar\ell_2(S_j,\mu)$ is ergodic. Hint: Let $S_1,S_2,\ldots,S_N$ be the atoms of the $\s$-algebra $\F^I$ of invariant sets.
Suppose $\mu$ is a probability measure on $S$ and $P_t$ is a semigroup on $L_p(S,\mu)$ satisfying the hypothesis of the Mean Ergodic Theorem. Prove that $P_t$ is ergodic iff there is a dense subset $D$ such that for all $f\in D$: $Qf=\int f\,d\mu$.
Point-wise Convergence
E. Hopf's maximal theorem and Birkhoff's ergodic theorem
Suppose $t\mapsto f_t$ is an integrable function from $\R_0^+$ into $L_p(S,\mu)$. Then there is a measurable mapping $F:\R_0^+\times S\rar\R$, such that for $\l$-almost all $t\in\R_0^+$: $F(t,.)=f_t$ and for $\mu$ almost all $x\in S$: $$ \int_0^t F(s,x)\,ds =\Big(\int_0^t f_s\,ds\Big)(x)~. $$ (cf. section). Thus the mapping $$ t\mapsto\Big(\int_0^t f_s\,ds\Big)(x)=\int_0^tF(s,x)\,ds $$ is for $\mu$-almost all $x\in S$ continuous. Therefore the sup over all $t\in\R^+$ is the same as the sup over all $t\in\Q^+$. Now if $P_t$ is a continuous contraction semigroup in $L_p(\mu)$, then we may define for any $f\in L_p(\mu)$: $$ f^* \colon=\sup_{t\in\R^+}|A_tf| =\sup_{t\in\Q^+}|A_tf| $$ $f^*$ is called the maximal function of the family $A_tf$, $t\geq0$. The power horse of ergodic theory is the following theorem. For a comprehensive proof we refer to N. Dunford and J.T. Schwartz, Linear Operators I. We present a proof in case $P_tf=f\circ\theta_t$ for some semigroup of transformations $\theta_t:S\rar S$ which leave the measure $\mu$ invariant; it follows that $P_t$ is a positive contraction semigroup on $L_1(S,\mu)$ and we further assume that it's continuous on $L_1(\mu)$. The central part of our proof is F. Riesz' Rising Sun Lemma $\proof$ The following picture and proof are taken from wikipedia: the sun shines horizontally from the right onto the sub-graph $\{(t,s):s\leq g(t)\}$ of $g$. $t\in U(g)$ if and only if the point $(t,g(t))$ is in the shadow of the sub-graph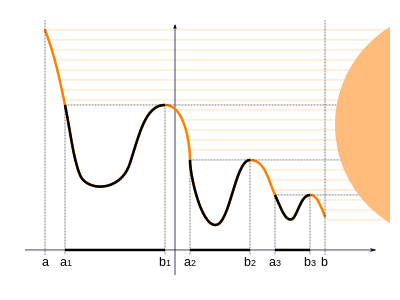
Now assume $[a,b)\sbe U(g)$, then we claim that $g(a) < g(b)$, for if $g(a)\geq g(b)$ then $g$ attains a maximum at some point $c\in[a,b)$ and there is a point $d > c$ such that $g(d) > g(c)$. Now if $d\leq b$ then $g$ doesn't attain its maximum on $[a,b)$ in $c$. Hence $d > b$ and since $g(b)\leq g(c) < g(d)$ it follows that $b\in U(g)$, which is a contradiction. Hence $g(a) < g(b)$. By continuity of $g$ this proves that in any case $g(a_n)\leq g(b_n)$. $\eofproof$
Suppose $g:\R_0^+\rar\R$ is cadlag, i.e. $g$ is right-continuous with left limits:
$$
\lim_{t\dar a}g(t)=g(a)
\quad\mbox{and}\quad
\lim_{t\uar a}g(t)=\colon g(a-)
\quad\mbox{exists.}
$$
Then $U(g)$ is the disjoint union of intervals of the form $(a_n,b_n)$ or $[a_n,b_n)$. Moreover for all $n$: $g(a_n) \leq g(b_n-)$.
The following result is just the particular case $P_u=L_u$ of the Maximal Theorem, where $L_u$ is the translation group $L_uf(t)=f(u+t)$:
$\proof$
Assume w.l.o.g. $f\geq0$. $\bar f(t) > \e$ if and only if there is some $s > t$ such that
$$
\int_t^sf(u)\,du > (s-t)\e~.
$$
So put $g(t)\colon=\int_0^tf(u)-\e\,du$, then $g$ is continuous and $\bar f(t) > \e$ iff for some $s > t$: $g(s) > g(t)$, i.e. iff $t\in U(g)$. By the Rising Sun Lemma:
$$
\int_{\bar f > \e}f-\e\,d\l
=\int_{U(g)}f-\e\,d\l
=\sum_{n=0}^\infty\int_{a_n}^{b_n}f-\e\,d\l
=\sum_n(g(b_n)-g(a_n))\geq0~.
$$
$\eofproof$
We remark that the inequality is almost an equality, for only in case $0\in U(g)$ there can be one summand, which could be strictly positive. Also $\R^+$ can be replaced with any bounded or unbounded interval!
Suppose $f\in L_1([0,1])$ and $\int_0^1 f\leq C$. Then there are pairwise disjoint intervals $(a_j,b_j)$ such that (suggested solution)
$$
\frac1{b_j-a_j}\int_{a_j}^{b_j}f(t)\,dt=C
\quad\mbox{and}\quad
\forall t\notin\bigcup(a_j,b_j):\quad\frac1t\int_0^tf(s)\,ds\leq C~.
$$
The following lemma is actually a bit stronger than theorem. As for the proof we'd like to remark that it only uses the invariance of $\mu$, Fubini and lemma, which is a consequence of the Rising Sun Lemma.
$\proof$
Suppose $f:S\rar\R_0^+$ is measurable and bounded. For $x\in S$ and
$M > 0$ put $f_M^*\colon=\sup\{A_tf:t\leq M\}$ and
$$
f_{M,x}(t)\colon=\left\{
\begin{array}{cl}
f(\theta_t(x))&\mbox{if $t\leq M$}\\
0&\mbox{otherwise,}
\end{array}
\right.
$$
Now for all $N > M$ and all $t\leq N-M$:
$$
f_M^*(\theta_t(x))
=\sup_{0 < s\leq M}\Big\{\frac1s\int_t^{t+s}f(\theta_u(x))\,du\Big\}~.
$$
Since $N-t\geq M$ we infer that:
\begin{eqnarray*}
f^*(\theta_t(x))
\geq\cl{f_{N,x}}(t)
&\colon=&\sup\Big\{\frac1s\int_0^s f_{N,x}(u+t)\,du: s\leq N-t\Big\}\\
&=&\sup\Big\{\frac1s\int_0^s f(\theta_{u+t}(x))\,du: s\leq N-t\Big\}\\
&\geq&\sup\Big\{\frac1s\int_0^s f(\theta_{u+t}(x))\,du: s\leq M\Big\}
=f_M^*(\theta_t(x))
\end{eqnarray*}
Now $\mu$ is $\theta_t$-invariant and thus: $\mu(f_M^*\circ\theta_t > \e)=\mu(f_M^* > \e)$; by exam and lemma we therefore conclude that:
\begin{eqnarray*}
\e\,\mu(f_M^* > \e)
&=&\frac\e{N-M}\int_0^{N-M}\mu(f_M^*\circ\theta_t>\e)\,dt\\
&=&\frac\e{N-M}\l\otimes\mu(\{(t,x)\in(0,N-M]\times S:f_M^*(\theta_t(x)) > \e\})\\
&\leq&\frac\e{N-M}\l\otimes\mu(\{(t,x)\in(0,N-M]\times S:\cl{f_{N,x}}(t) > \e\})\\
&\leq&\frac\e{N-M}\int_S\l(\{t > 0:\cl{f_{N,x}}(t) > \e\})\,\mu(dx)
\leq\frac1{N-M}\int_S\int_{[\bar f_{N,x} > \e]}f(\theta_t(x))\,dt\,\mu(dx)~.
\end{eqnarray*}
Since $\bar f_{N,x}(t)\leq f^*(\theta_t(x))$ we get for $A\colon=[f^* > \e]$:
$\{t:\bar f_{N,x}(t) > \e\}\sbe\{t:\theta_t(x)\in A\}$. Hence the last expression in the previous estimates is bounded from above by
$$
\frac1{N-M}\int_S\int_0^N I_A\circ\theta_t(x)f\circ\theta_t(x)\,dt\,\mu(dx)
$$
which, by Fubini and $\theta_t$-invariance of $\mu$ equals:
$$
\frac1{N-M}\int_0^N\int_S I_A\circ\theta_t(x)f\circ\theta_t(x)\,\mu(dx)\,dt
=\frac1{N-M}\int_0^N\int_A f\,d\mu
=\frac{N}{N-M}\int_A f\,d\mu~.
$$
By first letting $N\uar\infty$ and then $M\uar\infty$ we obtain the desired inequality.
$\eofproof$
Let $P_t$ be a semigroup satisfying the condition of theorem. Suppose $\vp:\R_0^+\rar\R_0^+$ is increasing, piece-wise smooth and $\vp(0)=0$. Put
$\Phi(t)\colon=\int_0^t\vp^\prime(2s)s^{-1}\,ds$, then
$$
\int\vp(f^*)\,d\mu\leq2\int_0^\infty\Phi(f^*)|f|\,d\mu
$$
$\proof$
By Fubini and theorem we get:
\begin{eqnarray*}
\int\vp(f^*)\,d\mu
&=&\int_0^\infty\vp^\prime(t)\mu(f^* > t)\,dt\\
&\leq&2\int_0^\infty\vp^\prime(t)t^{-1}\int_{[f^* > t/2]}|f(x)|\,\mu(dx)\,dt\\
&=&4\int_0^\infty\vp^\prime(2t)(2t)^{-1}\int_{[f^* > t]}|f(x)|\,\mu(dx)\,dt\\
&=&2\int_0^\infty\int_0^{f^*(x)}\vp^\prime(2t)t^{-1}|f(x)|\,dt\,\mu(dx)
=2\int_0^\infty\Phi(f^*)|f|\,d\mu
\end{eqnarray*}
$\eofproof$
Let $P_t$ be a semigroup satisfying the condition of theorem. Then we have:
$$
\Big(\int f^{*p}\,d\mu\Big)^{1/p}
\leq\left\{
\begin{array}{cl}
\frac{2^pp}{p-1}\norm f_p&\mbox{if $p > 1$}\\
\frac{e}{e-2}\Big(\mu(S)+\int|2f|\log^+|2f|\,d\mu\Big)&\mbox{if $p=1$}
\end{array}\right.
$$
where $\log^+x$ is the positive part of $\log x$, i.e. $\log^+ x\colon=\max\{0,\log x\}$.
$\proof$
1. For $p > 1$ this follows by lemma for $\vp(t)=t^p$ and Hölder ($1/p+1/q=1$):
\begin{eqnarray*}
\int f^{*p}\,d\mu
&\leq&\frac{p2^p}{p-1}\int f^{*p-1}|f|\,d\mu
\leq\frac{p2^p}{p-1}\Big(\int f^{*p}\,d\mu\Big)^{1/q}\norm f_p~.
\end{eqnarray*}
2. For $p=1$ we put $\vp(t)=(t-1)^+$, then $\Phi(t)=\log^+(2t)$ and thus
$$
\int(f^{*}-1)^+\,d\mu
\leq2\int_0^\infty\log^+(2f^*)|f|\,d\mu
$$
Now for $a,b\geq0$: $a\log^+b\leq a\log^+a+b/e$ and therefore
$$
\int(f^*-1)^+\,d\mu
\leq\int|2f|\log^+|2f|\,d\mu
+2e^{-1}\int f^*\,d\mu
$$
and thus:
$$
\int f^*\,d\mu
\leq\int(f^{*}-1)^+\,d\mu+\mu(S)
\leq\mu(S)+\int|2f|\log^+|2f|\,d\mu
+2e^{-1}\int f^*\,d\mu~.
$$
$\eofproof$
Given the inequality in proposition. Let $\vp:\R_0^+\rar\R_0^+$ be increasing, piece-wise smooth and $\vp(0)=0$. Put $\Phi(t)\colon=\int_0^t\vp^\prime(s)s^{-1}\,ds$, then
$$
\int\vp(f^*)\,d\mu\leq\int_0^\infty\Phi(f^*)|f|\,d\mu~.
$$
Given the inequality in proposition. For any $a > 0$ take $\vp(t)=(t-a)^+$. What inequality can be deduced? Find an optimal value for $a$ and show that (suggested solution)
$$
\Big(\Big(\int f^*\,d\mu\Big)^{1/2}-\Big(\frac{\mu(S)}{e}\Big)^{1/2}\Big)^2
\leq\int f\log^+f\,d\mu+\frac{\mu(S)}{e}~.
$$
Suppose $P_t=e^{tL}$ is a continuous contraction semigroup on $L_1(\mu)$ such that $P_t$ is a contraction on $L_\infty(\mu)$. For all $1\leq p < \infty$ and all $f\in L_p(\mu)$ we have in $L_p(\mu)$ and $\mu$-a.e:
$$
\lim_{t\to\infty}A_tf=Qf
$$
where $Q$ is the projection onto $\ker L$ and $\ker Q=\cl{\im L}$ (cf. Mean Ergodic Theorem).
$\proof$
By proposition $P_t$ is a continuous contraction semigroup on $L_p(\mu)$ for all $1\leq p < \infty$ and $A_tf$ converges in $L_p(\mu)$. Thus the set
$$
F_0
\colon=\{f+L_a g:\,f\in\ker L,a > 0,g\in L_p(\mu)\cap L_\infty(\mu)\}
$$
is a dense subset of $L_p(\mu)$ by the Mean Ergodic Theorem. Every function in $F_0$ can be written as $h=f+L_a g$ for some $f\in\ker L$ and some $g\in L_p(\mu)\cap L_\infty(\mu)$.
$$
A_th-f
=\frac1t\Big(\int_t^{t+a}P_sg\,ds-\int_0^{a}P_sg\,ds\Big)
\quad\mbox{i.e.}\quad
\norm{A_th-f}_\infty\leq\frac{2a}t\norm g_\infty~.
$$
Hence $A_th$ converges $\mu$-a.e. to $f$.Now take any $f\in L_p(\mu)$, then for all $\e > 0$ there is some $h\in F_0$ such that $\norm{f-h}_p < \e$ and by theorem for $p=1$ and corollary and Chebyshev's inequality for $p > 1$: $$ \mu\Big(\sup_t|A_t(f-h)| > r\Big)\leq c(p)r^{-p}\e^p~. $$ This implies that \begin{eqnarray*} \mu(\limsup_t|A_tf-Qf| > 3r) &\leq&\mu(\limsup_t|A_tf-A_th| > r) +\mu(\limsup_t|A_th-Qh| > r) +\mu(|Q(h-f)| > r)\\ &\leq&\mu(\sup_t|A_t(f-h)| > r) +\mu(\limsup_t|A_th-Qh| > r) +\mu(|Q(h-f)| > r)\\ &\leq&c(p)r^{-p}\e^p+0+\e^p r^{-p} \end{eqnarray*} where we used Chebyshev's inequality in the last step: $\mu(|g| > r)\leq r^{-p}\norm g_p^p$ and the fact that $Q$ is a contraction on $L_p(\mu)$. As $\e > 0$ was arbitrary we conclude that for all $r > 0$: $$ \mu(\limsup_t|A_tf-Qf| > 3r)=0 \quad\mbox{i.e. $A_tf$ converges $\mu$-a.e. to $Qf$} $$ $\eofproof$ The subsequent exam shows that we may have utilized the fifth assertion in the Mean Ergodic Theorem to prove the first part of Birkhoff's Ergodic Theorem.
Prove by means of proposition and proposition that under the assumptions of theorem the subspace $F\colon=\dom L\cap L_\infty(\mu)$ is a core for $L$. 2. Conclude that $\ker L+L(F)$ is dense and for all $f=Lg\in L(F)$ we have: $\norm{A_tf}_\infty\leq2\norm g_\infty/t$. Suggested solution.
The last argument in the proof of theorem can be easily generalized in the following way:
For $f\in L_p(\mu)$, $r,\e>0$ and $g\in D$, such that $\norm{f-g}_p<\e$ we have
$$
\limsup_n|T_n(f)-T(f)|
\leq\limsup_n|T_n(f)-T_n(g)|
+\limsup_n|T_n(g)-T(g)|
+|T(f)-T(g)|,
$$
Chebyshev's inequality and the assumptions now imply that
\begin{eqnarray*}
\mu(\limsup_n|T_n(f)-T(f)| > 3r)
&\leq&\mu(\limsup_n|T_n(f)-T_n(g)| > r)
+\mu(\limsup_n|T_n(g)-T(g)| > r)+\mu(T(|f-g|) > r)\\
&\leq&\mu(|f-g|^* > r)+0+\norm{T(|f-g|)}_p^pr^{-p}~.
\end{eqnarray*}
Convergence a.e. at $0$
For a continuous contraction semigroup $P_t:L_p(\mu)\rar L_p(\mu)$ we have $\lim_{t\dar0}\Vert P_tf-f\Vert=0$ and thus $\lim_{t\dar0}\Vert A_tf-f\Vert=0$. Hence it's obvious to ask if this limit exists a.e. Just employing the above method yields the following: In the particular case of a complete vector field $X$ on e.g. $\R^d$ with $\divergence X=0$ we have for all $f\in L_1(\R^d)$ and for $\l$-almost all $x\in\R^d$: $$ \lim_{t\dar0}\frac1t\int_0^tf(\theta_s(x))\,ds=f(x), $$ for this holds evidently for continuous functions $f$ of compact support. In case $X=\pa_x$ and $X=-\pa_x$ on $\R$ this is Lebesgue's Differentiation Theorem: for all $f\in L_1(\R)$ and $\l$-almost all $x\in\R$: $$ \lim_{t\to0}\frac1t\int_0^t f(x+s)\,ds=f(x)~. $$
Use exam to prove that for $\mu$-almost all $t\in\R$:
$$
\lim_{s\dar0}\frac1{\mu((t,t+s))}\int_{t}^{t+s} f(u)\,\mu(du)=f(t)~.
$$
for any Radon measure $\mu$ on $\R$ satisfying $\mu(\{t\})=0$ for all $t\in\R$.
Also $P_tf$ converges for e.g. reversible Markov processes a.e. to $f$ (as $t\dar 0$). The corresponding maximal inequality for reversible Markov chains is given in theorem. Cf. e.g. E.M. Stein, Topics in Harmonic Analysis etc..
Some corollaries
If not otherwise stated we will assume for this subsection that $\mu$ is a probability measure and $P_t$ is a positive and conservative, continuous contraction semigroup on $L_1(\mu)$ such that $P_t$ is a contraction on $L_\infty(\mu)$. We remark that conservativity is a weaker condition than $P_t$-invariance of $\mu$. In terms of dynamical systems: Suppose $(S,\F,\mu,\theta)$ is a dynamical system with invariant probability measure $\mu$. If $P_nf=f\circ\theta^n$ is ergodic, then by Birkhoff's Ergodic Theorem for $\mu$ almost all $x\in S$: $$ \lim_{n\to\infty}\frac1n\sum_{k=0}^{n-1}f\circ\theta^k(x)=\int f\,d\mu~. $$ In particular for $A\in\F$ and $f=I_A$ we put $$ \t_n(x,A)\colon=|\{k < n:\,\theta^k(x)\in A\}|~. $$ Then for $\mu$ almost all $x\in S$: $$ \lim_{n\to\infty}\frac1n\t_n(x,A) =\lim_{n\to\infty}\frac1n\sum_{k=0}^{n-1}P_kI_A(x) =\mu(A)~. $$ This means that the mean time spent by $\theta^k$ in $A$ (the mean sojourn time) is the measure of $A$. By proposition $\Theta(x)\colon=x+2\pi h$ is ergodic. The last statement follows from the Mean Ergodic Theorem and the fact that $\Theta$ is an isometry and thus by the Arzelà-Ascoli Theorem the sequence of functions $f\circ\Theta^k$ is relatively compact in $C(\TT^d)$ for all $f\in C(\TT^d)$. The event $k_r=k$ occurs if and only if $k10^r\leq a2^n < (k+1)10^r$. Define $\theta\colon=\log_{10}2$ and $x\colon=\log_2a\,\modul(1)$, then this happens iff $$ \log_{10}k\leq \log_2a+n\theta-r < \log_{10}(k+1) \quad\Lrar\quad \log_{10}k\leq x+n\theta(\modul1) < \log_{10}(k+1)~. $$ Now the transformation $\Theta:x\mapsto x+\theta(\modul1)$ is ergodic by proposition (for $\theta$ is an irrational number) on the probability space $([0,1),\l)$. Putting $A=[\log_{10}k,\log_{10}(k+1))$ we get: $$ \t_n(x,A) \colon=|\{k < n:\,\Theta^k(x)\in A\}| =|\{k < n:\mbox{the leading coefficient of $2^n$ is $k$}\}|~. $$ Since $\Theta$ is ergodic we conclude by the previous example that for almost all $x\in(0,1)$: $$ \lim_{n\to\infty}\frac{\t_n(x,A)}n =\l(A) =\log_{10}(1+1/k) $$ In probability the discrete version of corollary is stated as follows: For the particular case of the shift operator of a Markov chain $(X_n,\F_n,\P^x)$ in $S$ with invariant probability measure $\mu$ on $S$ we get that for all $\F^X$-measurable $F\in L_p(\O,\P^\mu)$ the sequence $$ \frac1n\sum_{k=0}^{n-1}F\circ\Theta^k $$ converges $\P$-a.s. and in $L_p(\P)$ to $\E(F|\F^I)$. Here $\F^I$ is a sub-$\s$-algebra of the $\s$-algebra $\F$ on $\O$: $\F^I=\{A\in\F:[\Theta\in A]=A\}$. For the special case of exam and $F(x_0,x_1,\ldots)=x_0$ this corollary is exactly the celebrated law of large numbers. Computationally this is definitely an improvement over the convergence of the sequence $$ \frac1n(f+Pf+\cdots+P^{n-1}f) $$ because computing e.g. $Pf$ is usually much more involved than computing $\int f\,d\mu$. However the computation of the sequence $$ \frac1n(f(X_0)+\cdots+f(X_{n-1})) $$ is almost trivial point-wise: we start with some point $X_0$ and choose the sequence of random points $X_1,X_2,\ldots$ according to the Markovian transition function. Of course we need to know one important property, which will be proved in subsection: the shift operator $\Theta$ of a reversible Markov chain is ergodic on $(\O,\P^\mu)$ provided the Markov operator is ergodic. $\proof$ Put $\O=\N^\N$, $\P$ the probability measure on $\O$, such that $N_k:\O\rar\N$, $N_k(\o)=\o_k$, are i.i.d. Put $\Theta(\o_1,\ldots)\colon=(\o_2,\ldots)$, then for all $F:S\times\O\rar\R$: $$ \Vert F\Vert_p^p =\int_S\int_\O |F(x,\o)|^p\,\P(d\o)\,\mu(dx) =\int_S\int_\O |F(x,N_1,N_2,\ldots)|^p\,d\P\,\mu(dx)~. $$ Now define a linear operator $T:L_p(\mu\otimes\P)\rar L_p(\mu\otimes\P)$ by $$ TF(x,\o)\colon=P_{\o_1}F_{\Theta(\o)}(x) $$ where $F_\o(x)\colon=F(x,\o)$. It follows that $$ \Vert TF\Vert_p^p =\sum_k\P(N_1=k)\Vert P_kF_{N_2,\ldots}\Vert_p^p \leq\sum_k\P(N_1=k)\Vert F(.,N_2,\ldots)\Vert_p^p =\Vert F(.,N_2,\ldots)\Vert_p^p =\Vert F\Vert_p^p~. $$ Moreover by definition $$ T^2F(x,\o) =P_{\o_1}TF(\Theta(\o),x) =P_{\o_1}P_{\o_2}F_{\Theta^2(\o)}(x) $$ and by induction on $n\in\N$: $$ T^nF(x,\o)=P_{\o_1}\ldots P_{\o_n}F_{\Theta^n(\o)}(x)~. $$ Corollary implies that $n^{-1}\sum_{k=1}^n T^kF(x,\o)$ converges $\mu\otimes\P$-a.e. By Fubini there is a subset $A\sbe\N^\N$ of probability $1$ such that for all $\o\in A$ this sequence converges $\mu$-a.e. on $S$. The assertion is the particular case $F(x,\o)=f(x)$. $\eofproof$Subordinated semigroups
The following result is about subordinated semigroups. We again refer to E.B. Davies, One-Parameter Semigroups! $\proof$ 1. We may assume w.l.o.g. that $f\geq0$. Since $P_tf=\ttd t(tA_tf)$, integration by parts yields for all $T > t_0$: \begin{eqnarray*} \int_0^T P_tf\vp(t)\,dt &=&TA_Tf\vp(T)+\int_0^T A_tf\,t(-\vp^\prime(t))\,dt\\ &\leq&f^*\Big(T\vp(T)+\int_{t_0}^T t(-\vp^\prime(t))\,dt\Big)\\ &=&f^*\Big(t_0\vp(t_0)+\int_{t_0}^T \vp(t)\,dt\Big)~. \end{eqnarray*} 2. Suppose $\a\in(0,1)$. If $\vp_1(s)$ is the density of an $\a$-stable probability measure $\mu_1(ds)=\vp_1(s)\,ds$ on $\R^+$, then $$ P_t^\a f\colon =\int_0^\infty P_sf\,\mu_t(ds) =\int t^{-1/\a}\vp_1(st^{-1/\a})\,P_sf \,ds~. $$ In this case we have $\vp(s)=t^{-1/\a}\vp_1(st^{-1/\a})$ and thus $$ t_0\vp(t_0)+\int_{t_0}^\infty\vp(s)\,ds\leq\sup_{s > 0}s\vp_1(s)+1~. $$ $\eofproof$ This also implies (cf. e.g. exam) that for all $f\in L_1(\mu)$ $P_t^\a f$ converges a.e. to $f$ as $t$ converges to $0$, provided there is a dense subspace of functions $f$ for which $P_t^\a f$ converges a.e. to $f$ as $t$ converges to $0$. In particular for $\a=1/2$ and $u(t)\colon=P_t^{1/2}f$ ($P_t^{1/2}$ is called the Cauchy semigroup) we have $$ \pa_t^2u(t)=(-H^{1/2})^2u(t)=Hu(t)~. $$ Hence if $H=\D$ is the Laplacian on some Riemannian manifold $M$ $u(t)$ is the harmonic extension of $f:M\rar\R$ on the Riemannian product manifold $\R^+\times M$. In this case $u(t)$ converges for all $f\in L_p(M)$ in $L_p(M)$ and a.e. to $f$ as $t\dar0$. Beware! if $M=S^{d-1}$, then $u$ is harmonic on $\R^+\times S^{d-1}$ but this is not the harmonic extension in spherical coordinates of a function on $S^{d-1}$ into e.g. the interior $B^d$, because the Riemannian product manifold $\R^+\times M$ is not isometric to $\R^d\sm\{0\}$ or the Laplacian on $\R^d$ in spherical coordinates is not $-\pa_r^2$ plus the Laplacian on $S^{d-1}$. The harmonic extension of a function on $S^{d-1}$ into e.g. the interior $B^d$ is given by the Poisson semigroup. However, if $M=\R^d$, then $u(t,x)=P_t^{1/2}f(x)$ is the harmonic extension of $f$ into $\R^+\times\R^d$ as a subset of $\R^{d+1}$. In this case the Riemannian product manifold $\R^+\times\R^d$ is isometric to the subset $\R^+\times\R^d$ of $\R^{d+1}$!
For $\a=1/2$ and $H=\D$ the Laplacian on $\R^d$ we have (cf. exam): $\vp_1(s)=e^{-1/4s}/\sqrt{4\pi s^3}$ and
$$
P_t^{1/2}f=C_t*f,
\quad\mbox{where}\quad
C_t(x)
=\frac{\G(\frac{d+1}2)}{\pi^{\frac{d+1}2}}
\frac{t}{(t^2+\Vert x\Vert^2)^{\frac{d+1}2}}~.
$$
denotes the Cauchy kernel. Suggested solution. Moreover:
$$
\sup_{s > 0}\frac{e^{-1/4s}}{\sqrt{4\pi s}}
=\frac1{\sqrt{2\pi e}}~.
$$
Take the translation group $P_tf(x)\colon=f(x+t)$, let $K_n\in L_1(\R)$, $n\in\N$, be any sequence of integrable functions and define convolution operators
$$
Q_nf\colon=\int_\R K_n(t)P_tf\,dt
$$
If $|K_n(t)|\leq n\b(tn)$ for some decreasing function $\b:\R_0^+\rar\R_0^+$ satisfying $\int_0^\infty\b(t)\,dt=C < \infty$. Adjust the proof of corollary to show that
$$
\sup_n|Q_nf|\leq2Cf^*~.
$$
Prominent examples for $K_n(t)$:
$$
\frac{n}{\sqrt{\pi}}e^{-(nt)^2},\quad
ne^{-nt}I_{(0,\infty)}(t),\quad
\frac{n}{\pi}\Big(\frac{\sin(nt)}{nt}\Big)^2~.
$$
Ergodic, Mixing and Exact Semigroups
The set of invariant measures
Let $M_1(S)$ be the set of all Borel probability measures on $S$, $\theta:S\rar S$ measurable and ${\cal M}\colon=\{\mu\in M_1:\,\mu_\theta=\mu\}$ the set of all $\theta$-invariant probability measures.
A point $x$ of a convex subset of a vector space is said to be an extremal point of $C$ if $y,z\in C$ and $x=(y+z)/2$ implies $x=y=z$, cf. e.g. wikipedia.
The permutation matrices are exactly the set of extreme points of the set of doubly stochastic matrices. This is known as the Birkhoff-von Neumann Theorem. For a proof cf. e.g. wikipedia.
$\proof$
2. If $\theta^{-1}(A)=A$, then by ergodicity: $\mu(A)\in\{0,1\}$. Hence $\nu(A)\in\{0,1\}$ and therefore $\theta$ is also ergodic with respect to $\nu$. By corollary for all $A\in\F$ the sequence:
$$
\frac1n\sum_{j=1}^nI_A\circ\theta^n
$$
converges $\mu$-a.e and $\nu$-a.e. to $\mu(A)$ and $\nu(A)$, respectively, i.e. $\mu(A)=\nu(A)$.3. Suppose $\nu,\mu\in{\cal M}$. If $\theta$ is ergodic with respect to $\l\colon=\tfrac12(\mu+\nu)$, then by 2. $\theta$ is ergodic with respect to both $\mu$ and $\nu$ and $\mu=\l=\nu$.
4. If $\mu$ is an extremal point of ${\cal M}$ and if there is a subset $A\in\F$, such that $\theta^{-1}(A)=A$ and $\mu(A)\in(0,1)$, then $$ \mu_1(B)\colon=\mu(B\cap A)/\mu(A) \quad\mbox{and}\quad \mu_2(B)\colon=\mu(B\cap A^c)/\mu(A^c) $$ are probability measures in ${\cal M}$ and $\mu=\mu(A)\mu_1+\mu(A^c)\mu_2$. $\eofproof$ For a compact space $S$ and a continuous transformation $\theta:S\rar S$ the set ${\cal M}$ is not empty (cf. exam) and weak * compact and by the Krein-Milman Theorem it's the closed convex hull of its extremal points. Hence any continuous transformation $\theta:S\rar S$ on a compact space $S$ admits an invariant probability measure $\mu$ such that $\theta$ is ergodic with respect to $\mu$.
Ergodic, mixing and exact semigroups
For the reminder of this subsection we will assume that $\mu$ is a probability measure and $P_t$ is a positive, continuous contraction semigroup on $L_1(\mu)$ such that $P_t$ is a contraction on $L_\infty(\mu)$. Moreover we assume that $\mu$ is $P_t$ invariant. This implies that $P_t$ is conservative.If $P_t$ is ergodic, then for all $f\in L_\infty(\mu)$: $A_tf$ converges in $L_1(\mu)$ to the constant function $\int f\,d\mu$ and thus for all $g\in L_\infty(\mu)$: $$ \lim_{t\to\infty}\int A_tf.g\,d\mu =\int \lim_{t\to\infty}A_tf.g\,d\mu =\int f\,d\mu\int g\,d\mu~. $$
$P_t$ is said to be mixing and exact, respectively, if for all $f,g\in L_\infty(\mu)$:
$$
\lim_{t\to\infty}\Big|\int\Big(P_tf-\int f\,d\mu\Big)g\,d\mu\Big|=0
\quad\mbox{and}\quad
\lim_{t\to\infty}
\sup_{0\leq f\leq1}\Big|\int\Big(P_tf-\int f\,d\mu\Big)g\,d\mu\Big|=0~.
$$
For convenience let us write $\la f\ra$ for $\int f\,d\mu$ and $\la f,g\ra\colon=\int fg\,d\mu$. $P_t$ is mixing iff for all $f,g\in L_\infty(\mu)$:
$$
\lim_{t\to\infty}\la P_tf,g\ra=\la f\ra\la g\ra~.
$$
Verify that all semigroups in exam are mixing.
$\proof$
We only prove the last statement, so suppose $f\geq0$ and w.l.o.g. $f\leq1$: $t\mapsto I_{[f > t]}=\colon F(t)$ is measurable, since $(t,x)\mapsto I_{[f > t]}(x)$ is $1$ iff $f(x) > t$ and thus it's the indicator function of the sub-graph $\{(t,x):0\leq t < f(x)\}$ of $f$; by e.g. exam $F$ is measurable. For bounded $f$ it is also integrable because $\norm{F(t)}_p=\mu(f > t)^{1/p}\leq1$ and since $f\leq 1$:
$$
\int_0^\infty\norm{F(t)}_p\,dt
=\int_0^1\norm{F(t)}_p\,dt\leq 1~.
$$
Finally we get for all $g\in L_q(\mu)$, $1/p+1/q=1$, by proposition (applied to the continuos linear functional $A(h)=\int gh\,d\mu$) and Fubini:
$$
\int g\int_0^\infty I_{[f > t]}\,dt\,d\mu
=\int_0^\infty\int_{f > t}g\,d\mu\,dt
=\int\int_0^fg\,dt\,d\mu
=\int fg\,d\mu~.
$$
$\eofproof$
$\proof$
1. If $P_t$ ergodic, then the condition stated above holds, for $I_A,I_B\in L_\infty(\mu)$. Conversely assume $P_tI_A=I_A$, then
$$
\mu(A)=
\frac1t\int_0^t\int_A P_tI_A\,d\mu
\rar\mu(A)^2,
\quad\mbox{i.e.}\quad\mu(A)\in\{0,1\}~.
$$
2. Assume w.l.o.g $0\leq f,g\leq1$. By the pancake formula and proposition we infer that $P_tf=\int_0^1 P_tI_{[f > u]}\,du$ (in e.g. $L_2(\mu)$) and thus
$$
\la P_tf-\la f\ra,g\ra
=\int_0^1\int_0^1
\la P_tI_{[f > u]}-\mu(f > u),I_{[g > v]}\ra\,du\,dv,
$$
and by bounded convergence: $\lim_{t\to\infty}\la P_tf-\la f\ra,g\ra=0$.3. In this case we get \begin{eqnarray*} \sup_{0\leq f\leq1}|\la P_tf-\la f\ra,g\ra| &\leq&\sup_{0\leq f\leq1}\int_0^1\int_0^1 |\la P_tI_{[f > u]}-\mu(f > u),I_{[g > v]}\ra|\,du\,dv\\ &\leq&\int_0^1\sup_{B\in\F} |\la P_tI_B-\mu(B),I_{[g > v]}|\,dv \end{eqnarray*} and the assertion follows again by bounded convergence. $\eofproof$ For all $A\in\F$ the set ${\cal B}$ of subsets $B\in\F$ such that $$ \lim_{t\to\infty}\frac1t\int_0^t\int_A P_sI_B\,d\mu\,ds=\mu(A)\mu(B) $$ is a $\l$-system (cf. appendix): Suppose $B_n\in{\cal B}$ and $B_n\uar B$, then in e.g. $L_1(\mu)$: $\norm{A_tI_{B_k}-A_tI_B}_1\leq\mu(B\sm B_k)$. Since the limits $\lim_{t\to\infty}A_tI_{B_k}$ and $\lim_{t\to\infty}A_tI_B$ exist in $L_1(\mu)$, we get by integrating over $A$: \begin{eqnarray*} \Big|\mu(B_k)\mu(A)-\lim_{t\to\infty}\int_AA_tI_B\,d\mu\Big| &=&\Big|\int_A\lim_{t\to\infty}A_tI_{B_k}\,d\mu -\int_A\lim_{t\to\infty}A_tI_B\,d\mu\Big|\\ &\leq&\int_A\Big|\lim_{t\to\infty}A_tI_{B_k}-\lim_{t\to\infty}A_tI_B\Big|\,d\mu \leq\mu(B\sm B_k)~. \end{eqnarray*} Now, as $k\to\infty$, it follows that: $\lim_{t\to\infty}\int_AA_tI_B\,d\mu=\mu(A)\mu(B)$, i.e. $B\in{\cal B}$. Thus if ${\cal B}$ contains a $\pi$-system ${\cal P}$, then ${\cal B}$ contains the $\s$-algebra generated by ${\cal P}$. Typical $\pi$-systems: The topology of $S$, i.e. the set of all open sets; all sets of the form $(-\infty,b_1]\times\cdots\times(-\infty,b_d]$ in $\R^d$; the collection of sets $\bigcup_n{\cal P}_n$ in subsection.
Suppose $P$ is an ergodic Markov operator with strictly positive invariant probability measure $\mu$ on a finite set $S$. Then for all $x,y\in S$ there is some $n\in\N$ such that $p^{(n)}(x,y) > 0$ - cf. exam. 2. $P$ is exact iff it is mixing and this holds if and only iff
$$
\forall x,y\in S:\quad
\lim_n p^{(n)}(x,y)=\mu(y)~.
$$
This means that the powers $P^n$ of the stochastic matrix $P$ converge to a matrix with identical columns. 3. Find a stochastic matrix $P\in\Ma(2,\R)$ such that $P$ is ergodic but not mixing.
The Markov operator in exam is exact.
Conductance
The following is taken from Random Walks in a Convex Body .... Let $Pf(x)=\int f(y)P(x,dy)$ be a reversible Markov chain with reversible probability measure $\mu$ and conductance $K$. By subsection this means that we have for all Borel sets $A\in\B(S)$: $$ Q(I_A)\geq K\mu(A)(1-\mu(A)), \quad\mbox{where}\quad Q(f)\colon=\la(1-P)f,f\ra $$ denotes the Dirichlet-form of $P$. $\proof$ 1. By exam we have for all $M\in\R$: $Q(f)\geq Q((f-M)^+)$.2. By Cauchy-Schwarz we get: \begin{eqnarray*} \int\int|f(y)^2-f(x)^2|P(x,dy)\,\mu(dx) &=&\int\int|f(y)-f(x)||f(y)+f(x)|P(x,dy)\,\mu(dx)\\ &\leq&2\norm f_2\Big(\int\int(f(y)-f(x))^2P(x,dy)\,\mu(dx)\Big)^{1/2} =2\norm f_2\sqrt{2Q(f)} \end{eqnarray*} 3. Now put $F_x(y)=f(y)^2-f(x)^2$. Then by integration by parts and Fubini we conclude that for all $f\in L_2(\mu)$: \begin{eqnarray*} \int\int|f(y)^2-f(x)^2|P(x,dy)\,\mu(dx) &=&2\int\int_{F_x > 0}F_x(y)P(x,dy)\,\mu(dx)\\ &=&2\int\int_{[F_x > 0]}F_x(y)P(x,dy)\,\mu(dx) =2\int\int_0^\infty P(x,F_x > t)\,dt\,\mu(dx)\\ &=&2\int\int_{f(x)^2}^\infty P(x,f^2 > t)\,dt\,\mu(dx) =2\int_0^\infty\int_{[f^2\leq t]}P(x,f^2 > t)\,\mu(dx)\,dt\\ &=&2\int_0^\infty\P^\mu(X_0\in[f^2\leq t],X_1\in[f^2 > t])\,dt\\ &\geq&2K\int_0^\infty\mu(f^2 > t)\mu(f^2\leq t)\,dt \end{eqnarray*} Here we may replace $\mu(f^2 > t)$ with $\mu(f^2\geq t)$, for the set $\{t:\mu(f^2=t) > 0\}$ has Lebesgue measure $0$. Replacing $f$ with $(f-M)^+$ and choosing a median for $M$ - i.e. $\mu(f\geq M),\mu(f\leq M)\geq1/2$ yields by 1.,2. and 3.: \begin{eqnarray*} \sqrt{2Q(f)} &\geq&\frac{K}{\norm{(f-M)^+}_2}\int_0^\infty\mu((f-M)^{+2}\geq t)\mu((f-M)^{+2}\leq t)\,dt\\ &\geq&\frac{K}{2\norm{(f-M)^+}_2}\int_0^\infty\mu((f-M)^{+2}\geq t)\,dt =\frac{K}{2}\norm{(f-M)^+}_2~. \end{eqnarray*} The same argument applies to $(f-M)^-$. As $\norm{f-\la f\ra}_2^2=\inf_s\norm{f-s}_2^2$ we infer that: $$ 2Q(f) \geq\frac{K^2}{4}\max\Big\{\norm{(f-M)^+}_2^2,\norm{(f-M)^-}_2^2\Big\} \geq\frac{K^2}{8}\norm{f-M}_2^2 \geq\frac{K^2}{8}\norm{f-\la f\ra}_2^2~. $$ $\eofproof$ Now we look at the Poissonization $P_t\colon=\E P^{N_t}=e^{-t(1-P)}$: for $f\in L_2(\mu)$ and $\la f\ra=0$ we put $u(t)\colon=\norm{P_tf}^2$ and conclude that $$ u^\prime(t) =-2\la(1-P)P_tf,P_tf\ra =-2Q(P_tf) \leq-\frac{K^2}{8}u(t) $$ Since $u(0)=\norm f^2$ it follows that $u(t)\leq e^{-K^2t/8}\norm f^2$. However for the simple powers of $P$ we don't have $\norm{P^nf-\la f\ra}\leq(1-c)^n\norm f$ for some constant $c\in(0,1)$: take the symmetric stochastic matrix (cf. exam) $$ P\colon= \left(\begin{array}{cc} 0&1\\ 1&0 \end{array}\right) $$ on a two point state space $S=\{1,2\}$. The reversible probability $\mu$ on $S$ is the uniform probability, i.e. $\mu(1)=\mu(2)=1/2$. As $K(1)=\P^\mu(X_0=1,X_1=2)=1/2=K(2)$, the conductance is $2$. On the other hand $P^2=1$. So we need an additional condition on $P$: we assume in addition $P$ being positive (definite) - the corresponding Markov chain is called 'lazy'. Positive definiteness implies that there is a bounded positive (definite) linear operator $R$ such that $R^2=P$. Proposition asserts that on the subspace $D$ orthogonal to the constant functions: $\la Pf,f\ra\leq(1-K/4)\norm f^2$ and consequently on $D$: $\norm{Rf}^2\leq(1-K/4)\norm f^2$. Induction on $n$ yields for all $f$ orthogonal to the constant functions: $$ \norm{R^nf}^2\leq(1-K/4)^n\norm f^2 \quad\mbox{hence}\quad \norm{P^nf}=\norm{R^{2n}f}\leq(1-K/4)^n\norm f~. $$ So we just arrived at the following The Markov operators in exam and exam are exact.
The terminal $\s$-algebra
Let us return to the case of a measure preserving map $\Theta$ on a probability space $(\O,\F,\P)$. We will moreover assume that $\Theta$ is onto. We say $\Theta$ is ergodic,mixing or exact if $Pf\colon=f\circ\Theta$ is ergodic,mixing or exact. Put $\F_n^\prime=\Theta^{-n}(\F)$, i.e. $\F_n^\prime$ is the $\s$-algebra generated by the mapping $\Theta^n$, the $n$-fold product of $\Theta$. For all $A\in\F$ we have $$ [\Theta^{n+1}\in A] =[\Theta\circ\Theta^n\in A] =[\Theta^n\in[\Theta\in A]]\in\F_n^\prime~. $$ Hence $\F_n^\prime$ is a decreasing sequence of $\s$-algebras.
The $\s$-Algebra
$$
\F^{T}
\colon=\bigcap_n\F_n^\prime=\bigcap_n\Theta^{-n}(\F)
$$
is called the terminal $\s$-algebra and every set in $\F^T$ is called a terminal event.
If $A\in\F$ is $\Theta$ invariant, then for all $n\in\N$: $A=[\Theta^n\in A]$ and thus $A\in\F^T$, i.e. $\F^I\sbe\F^T$. An event $A\in\F$ is terminal if and only if for all $n\geq0$ there is some subset $A_n\in\F$ such that $A=\Theta^{-n}(A_n)$; moreover in this case we conclude that
$$
\Theta^{-n}(A_n)
=A
=\Theta^{-n-m}(A_{n+m})
=\Theta^{-n}(\Theta^{-m}(A_{n+m}))~.
$$
Since $\Theta^n$ is onto this implies: $\Theta^{-m}(A_{n+m})=A_n$.
Let $(X_n,\F_n,\P^x)$ be a Markov chain in $S$, $A\in\F_n$, $B\in\F_n^\prime$. Prove that $\P^x(A\cap B|X_n)=\P^x(A|X_n)\P^x(B|X_n)$. Suggested solution.
If $\Theta:S^\N\rar S^\N$ is the Bernoulli shift, then the terminal $\s$-algebra is trivial.
$\proof$
Let $\F_n$ be the $\s$-algebra generated by the first $n$ projections $\Prn_1,\ldots,\Prn_n$. The $\s$-algebra $\F_n^\prime$ is the $\s$-algebra generated by the projections $\Prn_{n+1},\ldots$. Thus for all $A\in\F^{T}$ and all $B\in\bigcup_n\F_n$: $\P(A\cap B)=\P(A)\P(B)$. Now ${\cal L}_A\colon=\{B\in\F:\P(A\cap B)=\P(A)\P(B)\}$ is a $\l$-system containing the $\pi$-system $\bigcup\F_n$. By Dynkin's $\pi$-$\l$-Theorem: ${\cal L}_A=\F$ and consequently $\F$ is independent from $\F^{T}$; in particular $\F^T$ is independent from itself, i.e. $\P(A)\in\{0,1\}$.
$\eofproof$
$\proof$
Assume that $\F^T$ is trivial. Put for $B\in\F$: $C\colon=[\Theta^n\in B]\in\F_n^\prime$, then
\begin{eqnarray*}
|\P(A\cap[\Theta^n\in B])-\P(A)\P(B)|
&=&|\P(A\cap C)-\P(A)\P(C)|
=|\E(I_A-\P(A);C)|\\
&=&|\E(\E(I_A|\F_n^\prime)-\E I_A;C)|
\leq\E|\E(I_A|\F_n^\prime)-\E I_A|~.
\end{eqnarray*}
Since $\E(I_A|\F_n^\prime)$ is a reverse martingale and $\F^{T}$ is trivial, the sequence $\E(I_A|\F_n^\prime)$ converges by theorem in $L_1(\P)$ to $\E I_A=\P(A)$.Conversely, if $\Theta$ is exact and $A\in\F^{T}$, such that $\P(A)\in(0,1)$, then there is a sequence $A_n\in\F_n^\prime$, such that $A=\Theta^{-n}(A_n)$. Hence, by exactness: $$ |\P(A)-\P(A)^2| =\lim_{n\to\infty}|\P(A\cap\Theta^{-n}(A_n))-\P(A)\P(A_n)| =0~. $$