Discrete Dynamical Systems
In the sequel $(\O,\F,\mu)$ will always denote a $\s$-finite measure space. All spaces $S$ are more or less assumed to be Polish, i.e. there is some metric $d$ on $S$ such that $(S,d)$ is a complete and separable metric space. This ensures in particular that $S^\N$ is Polish and the Borel $\s$-algebra $\B(S^\N)$ on $S^\N$ coincides with the product $\s$-algebra, e.g. $F:\O\rar S^\N$ is measurable iff all components $\Prn_n\circ F$ are measurable. Moreover any finite Borel measure $\mu$ on $S$ is regular, i.e. for all Borel sets $A$ and all $\e > 0$ there is a compact set $K$ and an open set $U$, such that $K\sbe A\sbe U$ and $\mu(U\sm K) < \e$. It follows that e.g. bounded Lipschitz functions are dense in $L_p(\mu)$ for all $1\leq p < \infty$:
Put
$$
f(x)=\frac{d(x,U^c)}{d(x,U^c)+d(x,K)},
$$
then $f$ is Lipschitz, $f|K=1$, $f|U^c=0$ and for all $p > 0$: $\int|f-I_A|^p\,d\mu < \e$. Solution by T. Speckhofer
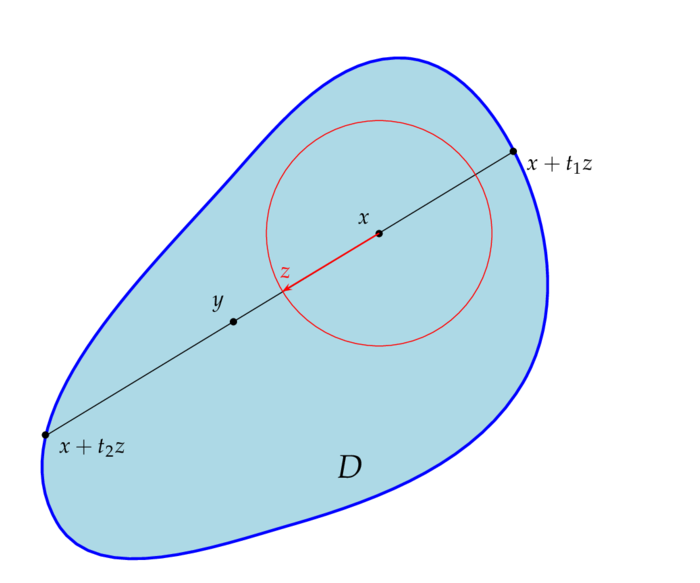
If $S=M$ is a (smooth) manifold (i.e. for convenience, a connected Polish space locally homeomorphic to a euclidean space with a differentiable structure). If you don't care about manifolds in general, open subsets of euclidean spaces suffice - though we assume that all manifolds don't have a boundary! The space $C_c^\infty(M)$ of smooth functions with compact support is dense in $L_p(\mu)$ for all $1\leq p < \infty$ and all Radon measures $\mu$ on $M$, i.e. $\mu$ is Borel and all compact subsets of $M$ have finite measure.
A measurable mapping $\theta:S\rar S$ is called measure preserving if for all $A\in\F$:
$\mu(\theta\in A)=\mu(A)$ i.e. the image measure $\mu_\theta$ of $\mu$ under $\theta$ equals $\mu$.
Thus $\theta$ is measure preserving, if $\mu$ is invariant under the mapping $\theta$. We will also say that $\mu$ is stationary under $\theta$ and call $(S,\F,\mu,\theta)$ a dynamical system. By the transformation theorem of measure theory $\theta:S\rar S$ is measure preserving if and only if for all $f\in L_1(\mu)$:
$$
\int f\circ\theta\,d\mu=\int f\,d\mu~.
$$
Suppose $\theta$ is measure preserving, then for all $f\in L_p(\mu)$ and all $n\in\N_0$ we define
$$
P_nf(x)\colon=f(\theta^n(x))
$$
where $\theta^0(x)\colon=x$. This is a simple example of what is known as a semigroup $P_n$ on $L_p(\mu)$; since $\theta$ is measure preserving, we have: $\norm{P_nf}_p=\norm f_p$, in particular $P_n$ is a contraction semigroup.
$\theta:(0,1)\rar(0,1)$ has an invariant measure with density $\r$ iff (cf. exam):
$$
\forall x\in(0,1):\quad
\sum_{y:\theta(y)=x}\frac{\r(y)}{|\theta^\prime(y)|}=\r(x)~.
$$
Put $\theta:\R\rar\R$, $\theta(x)=x-1/x$. Then the Lebesgue measure is $\theta$-invariant. Cf. example.
Put $S=[0,1)$ and $\theta(x)=ax(\modul1)$ for $a-1=1/a$, $a > 0$. Then Lebesgue measure is not invariant under $\theta$. Find a measure $\mu$ on $S$ invariant under $\theta$. Hint: Assume $\mu$ has constant density $m_1$ on $(0,1/a)$ and constant density $m_2$ on $(1/a,1)$. Suggested solution
Suppose $\mu$ is a Borel probability measure on the Polish space $S$ and let $\P$ be the product measure on $\O\colon=S^\N$. The so called shift operator $\Theta:\O\rar\O$ defined by $\Prn_n(\Theta(\o))=\o_{n+1}$ is obviously measurable (with respect to the product $\s$-algebra) and $\P$ is invariant under $\Theta$. $\Theta$ is also known as the Bernoulli shift and the dynamical system a Bernoulli scheme (cf. exam).
Since the Borel $\s$-algebra of $\O$ is generated by the projections $\Prn_n$, $n\in\N$, we only have to show that for all $A\in{\cal B}(S)$ and all $n\in\N$: $\P(\Theta\in[\Prn_n\in A])=\P([\Prn_n\in A])$. Now by definition $\P([\Prn_n\in A])=\mu(A)$ and since $\Prn_n\circ\Theta=\Prn_{n+1}$ we conclude that
$$
\P(\Theta\in[\Prn_n\in A])
=\P(\Prn_n\circ\Theta\in A)
=\P(\Prn_{n+1}\in A)
=\mu(A)~.
$$
Remark: In probability the projections $\Prn_n$ are independent and identically distributed $S$-valued random variables, a so called i.i.d. sequence in $S$ with distribution $\mu$.
On the set $S=[0,1]^2$ define
$$
\theta(x,y)=\left\{\begin{array}{cl}
(2x,y/2)&\mbox{if $x < 1/2$}\\
(2-2x,1-y/2)&\mbox{$x\geq1/2$}
\end{array}\right.
$$
Then the Lebesgue measure is invariant under $\theta$. The transformation $\theta$ is known as the folded baker transformation. Suggested solution. Solution by T. Speckhofer. The unfolded baker transformation $\theta:S\rar S$ is given by $\theta(x,y)=(2x-[2x],(y+[2x])/2)$, cf. e.g. wikipedia. Both the folded and the unfolded map are invertible!
The Gauß map
On the set $S=[0,1)$ define the Gauss map $\theta(x)=1/x-[1/x]$. Now let $\mu$ be the probability measure on $S$ with density $(\log 2)^{-1}(1+x)^{-1}$, then $\mu$ is $\theta$-invariant.
Let $\theta$ be the Gauss map. For real numbers $x_1,\ldots,x_k\geq1$ put
$$
\la x_1\ra\colon=\frac1{x_1}
\quad\mbox{and}\quad
\la x_1,\ldots,x_{k+1}\ra=\frac1{x_1+\la x_2,\ldots,x_{k+1}\ra}~.
$$
In particular:
$$
\la x_1,x_2\ra=\frac1{x_1+\frac1{x_2}},
\la x_1,x_2,x_3\ra=\frac1{x_1+\frac1{x_2+\frac1{x_3}}},\ldots
$$
Provided $\theta^k(x)\neq 0$ define for $x\in(0,1)$: $a_1,a_2,\ldots:(0,1)\rar\N$ by
$$
a_1(x)\colon=[1/x],\quad
a_{k+1}(x)\colon=[1/\theta^k(x)]~.
$$
The sequence $a_1(x),a_2(x),\ldots$ is called the continued fraction of $x$. Verify the following statements: (suggested solution)
- For all $x\in[0,1)$ and all $k\in\N$ such that $x,\theta(x),\ldots,\theta^{k-1}(x)\neq0$: $$ x=\la a_1(x),\ldots,a_k(x)+\theta^k(x)\ra \quad\mbox{and}\quad \theta(x)=\la a_2(x),\ldots,a_k(x)+\theta^k(x)\ra~. $$
- For $n_1,\ldots,n_k\in\N$ and $t\in(0,1)$: $$ \theta(\la n_1,\ldots,n_k+t\ra)=\la n_2,\ldots,n_k+t\ra~. $$
- Put $I=[0,1)\sm\Q$. For all $k\in\N$ we have $\theta^k(I)\sbe I$. Hence the functions $a_k:I\rar\N$ are defined for all $k\in\N$.
- For all $x\in[0,1)\cap\Q$ there is some $k\in\N$ such that $\theta^k(x)=0$. Conversely, if $\theta^k(x)=0$, then $x$ must be rational.
For $n_1,n_2,\ldots\in\N$ we put
\begin{eqnarray*}
I_{n_1}&\colon=&(\la n_1+1\ra,\la n_1\ra),\\
I_{n_1,n_2}&\colon=&(\la n_1,n_2\ra,\la n_1,n_2+1\ra),\\
I_{n_1,n_2,n_3}&\colon=&(\la n_1,n_2,n_3+1\ra,\la n_1,n_2,n_3\ra,
\quad\mbox{etc.}
\end{eqnarray*}
Then the following holds (suggested solution):
- $\theta$ is a homeomorphism from $I_{n_1,\ldots,n_k}$ onto $I_{n_2,\ldots,n_k}$.
- $I_{n_1,\ldots,n_k,n_{k+1}}\sbe I_{n_1,\ldots,n_k}$.
- For all $j\leq k$: $a_j|I_{n_1,\ldots,n_k}=n_j$.
- The open interval $I_{n_1,\ldots,n_k}$ has length at most $2^{-k}$. Thus if $a_j(x)=a_j(y)=n_j$ for all $j\leq k$, then $|x-y|\leq2^{-k}$.
An example on the real line
1. $\theta|(a_j,a_{j-1})$ is continuous, $\theta^\prime > 1$ and $$ \lim_{x\dar a_j}\theta(x)=-\infty,\quad \lim_{x\uar a_{j+1}}\theta(x)=\infty~. $$ Moreover $\lim_{x\to\pm\infty}\theta(x)=\pm\infty$.2. Fix $t\in\R$ and put $q(x)\colon=(x-x_0)\ldots(x-x_n)$, $p(x)\colon=(x-a_1)\ldots(x-a_n)=x^n-x^{n-1}\sum a_j+\cdots$ and $p_j(x)=p(x)/(x-a_j)$. Then \begin{eqnarray*} q(x) &=&(\theta(x)-t)p(x) =(x+\a-t)p(x)-\sum_{j=1}^nc_jp_j(x)\\ &=&x(x^n-x^{n-1}\sum a_j)+(\a-t)x^n+r(x), \end{eqnarray*} where $r$ is some polynomial of degree $n-1$ at most. Comparing the coefficients of $x^n$ we find: $$ -\sum_{j=0}^n x_j=-\sum_{j=1}^na_j+\a-t~. $$ Therefore $\theta:(a_j,a_{j+1})\rar\R$ is a diffeomorphism with inverse $x_j$ and by the transformation theorem of measure theory: $$ \int f\circ\theta\,d\l =\sum_{j=0}^{n+1}\int_{a_j}^{a_{j+1}}f(\theta(x))\,dx =\sum_{j=0}^{n+1}\int f(t)x_j^\prime(t)\,dt =\int f\,d\l~. $$
For $t > 0$ let $\mu_t$ be the measure on $\R^+$ with density
$$
x\mapsto\frac{t\,\exp(-t^2/4x)}{\sqrt{4\pi x^3}}~.
$$
Show that the Laplace transform $\o_t(y)\colon=\int_0^\infty e^{-xy}\,\mu_t(dx)$ is given by $\o_t(y)=e^{-t\sqrt y}$. 2. Conclude that $\mu_s*\mu_t=\mu_{s+t}$. The measures $\mu_t$ are called $1/2$-stable probability measures on $\R^+$ ($1/2$ refers to the square root of $y$ in $\o_t$). Suggested solution.
Homomorphic and isomorphic systems
A dynamical systems $(\wt S,\wt\F,\wt\mu,\wt\theta)$ is said to be homomorphic to $(S,\F,\mu,\theta)$, if there is a measurable mapping $F:(S,\F)\rar(\wt S,\wt\F)$ such that $\wt\mu=\mu_F$ and $\wt\theta\circ F=F\circ\theta$. If in addition $(S,\F,\mu,\theta)$ is also homomorphic to $(\wt S,\wt\F,\wt\mu,\wt\theta)$, then $(S,\F,\mu,\theta)$ and $(\wt S,\wt\F,\wt\mu,\wt\theta)$ are said to be isomorphic.
If $\mu$ is $\theta$-invariant, then $\mu_F$ is $\wt\theta$-invariant, because for all $B\in\wt\F$ we have by definition:
\begin{eqnarray*}
\mu_F(\wt\theta^{-1}(B))
&=&\mu(F^{-1}(\wt\theta^{-1}(B)))
=\mu((\wt\theta\circ F)^{-1}(B))
=\mu((F\circ\theta)^{-1}(B))\\
&=&\mu(\theta^{-1}(F^{-1}(B)))
=\mu(F^{-1}(B))
=\mu_F(B)~.
\end{eqnarray*}
Suppose $R$ is an equivalence relation on a Polish space $S$ such that $S/R$ is again Polish. Let $\pi:S\rar S/R$ be the quotient map. If a continuous map $\theta:S\rar S$ is constant on all sets $R(x)$, then there is a continuous map $\wh\theta:S/R\rar S/R$ such that $\wh\theta\circ\pi=\pi\circ\theta$. Finally, if $\mu$ is a $\theta$-invariant probability measure on $S$, then its image measure $\mu_\pi$ is $\wh\theta$-invariant.
For $S\colon=(0,1)$ and $\theta(x)=4x(1-x)$ let $\mu$ be the probability measure with density $f(x)=\pi^{-1}(x(1-x))^{-1/2}$. Then $\mu$, $\d_0$ and $\d_{3/4}$ are $\theta$-invariant. Moreover, put $F(x)=(\sin(\pi x)/2)^2$, then (suggested solution)
$$
F^{-1}\circ\theta\circ F(x)
=\left\{\begin{array}{cl}
2x&\mbox{if $x < 1/2$}\\
2(1-x)&\mbox{if $x\geq1/2$}
\end{array}\right.
$$
Let $S=\R^+$, $\mu(dx)=e^{-x}dx$ and $\theta(x)=-\log|1-2e^{-x}|$. Then $\mu$ is $\theta$-invariant. Suggested solution.
Recurrence
$\proof$ Let $B$ be the set of all $\o\in A$, such that for all $k\geq1$: $\theta^k(\o)\notin A$, i.e. $$ B \colon=A\cap\bigcap_{k\geq1}[\theta^k\in A^c] =A\cap\bigcap_{k\geq1}\theta^{-k}(A^c)~. $$ Then for all $n\geq1$: $B\cap\theta^{-n}(B)=\emptyset$, for $\theta^{-n}(B)\sbe\theta^{-n}(A)$ and $B\sbe\theta^{-n}(A^c)$. It follows that: $$ \forall m\neq n\qquad\theta^{-m}(B)\cap\theta^{-n}(B)=\emptyset $$ and thus the sets $[\theta^n\in B]$, $n\in\N$, are pairwise disjoint. Since all of these sets have equal probability this probability is necessarily zero. The same reasoning applied to $\theta^n$ instead of $\theta$ shows that $$ \forall n\in\N\qquad\P\Big(A\cap\bigcap_{k\geq1}[\theta^{nk}\in A^c]\Big)=0 \quad\mbox{i.e.}\quad \P\Big(A\cap\bigcup_n\bigcap_{k\geq1}[\theta^{nk}\in A^c]\Big)=0~. $$ Finally $$ \liminf_n[\theta^n\in A^c] =\bigcup_n\bigcap_{k\geq n}[\theta^k\in A^c] \sbe\bigcup_n\bigcap_{k\geq1}[\theta^{nk}\in A^c] $$ and therefore $\P\Big(A\cap\Big(\limsup_n[\theta^n\in A]\Big)^c\Big)=\P(A\cap\liminf_n[\theta^n\in A^c])=0$. $\eofproof$ Hence for $\P$ almost all $\o\in A$ there is an infinite number of $n\in\N$ such that $\theta^n(\o)\in A$; in other words the sequence $\theta^n(\o)$ hits $A$ infinitely many times!
Suppose $\theta$ is a measure preserving map on the probability space $(\O,\F,\P)$. Then for all $A\in\F$ (suggested solution):
$$
\limsup_n\P(A\cap[\theta^n\in A])\geq\P(A)^2~.
$$
The following result is a topological version of the previous proposition. Recall the following definitions from topology:
- A subset $G$ of a metric space $S$ is called a $G_\d$-set if it`s the intersection of a sequence of open sets.
- A basis for the topology of $S$ is a collection $U_\a$, $\a\in I$, of open subsets, such that for every open subset $V$ of $S$ there is a subset $J\sbe I$ such that $V=\bigcup_{\a\in J}U_\a$.
Suppose $\theta$ is measurable and $A\in\F$ satisfies $\mu(\theta^{-1}(A)\D A)=0$. Then there is a subset $B$ in the $\mu$-completion $\F^\mu$ of $\F$ such that $\mu(A\D B)=0$ and $\theta^{-1}(B)=B$. Suggested solution
For a measure space $(S,\F,\mu)$ and $A,B\in\F$ we will write $A=B$ if $\mu(A\D B)=0$.
If $\mu$ is finite then $\F$ can be seen as a subspace of $L_1(\mu)$: Prove that $\norm{I_A-I_B}_1=\mu(A\D B)$ and that $\F$ with the metric inherited from $L_1(\mu)$ is a complete metric space. Solution by T. Speckhofer
Ergodic transformations
Let $(S,\F,\mu)$ $\s$-finite measure space. A subset $A\in\F$ is said to be $\theta$-invariant, if $[\theta\in A]=A$. $\theta$ will be said to be ergodic on $(S,\F,\mu)$ if $A\in\F$ and $[\theta\in A]=A$ implies: $\mu(A)=0$ or $\mu(A^c)=0$.
We will mostly assume that $\mu$ is a probability measure; in this case $\theta$ is ergodic iff $[\theta\in A]=A$ implies: $\mu(A)\in\{0,1\}$.
When talking about ergodicity of a transformation $\theta$ with respect to a probability measure $\mu$ we implicitly assume that $\mu$ is $\theta$-invariant, i.e. $\theta$ preserves $\mu$!Suppose $\mu(S) < \infty$, then $\theta$ is ergodic if and only if the constant functions are the only functions $f\in L_p(\mu)$ such that $Pf=f$ and thus for all $n$: $P_nf=f$: If $\theta$ is not ergodic then there exists $A\in\F$ such that $\mu(A),\mu(A^c) > 0$ and $[\theta\in A]=A$; it follows that $PI_A=I_A$. Conversely if $Pf=f\circ\theta=f$ for some non-constant function $f$, then for all Borel sets $B$ in $\R$: $$ A \colon=[f\in B] =[f\circ\theta\in B] =[\theta\in[f\in B]] =[\theta\in A] $$
Suppose $S$ is a metric space. Then the space $C_b(S)$ of all bounded, continuous, real valued functions with $\norm f\colon=\sup\{|f(x)|:x\in S\}$ is a Banach space. 2. The subspace $C_{bu}(S)$ of all bounded and uniformly continuous functions is a closed subspace of $C_b(S)$. 3. If in addition $S$ is locally compact (i.e. every point has a compact neighborhood), then
$$
C_0(S)\colon=\{f\in C_b(S):\forall\e > 0\,\exists K\mbox{ compact: }|f|K^c| < \e\}
$$
is a closed subspace of $C_b(S)$. If $S$ is discrete we also write $c_0(S)$
If $S$ is separable and locally compact and $\theta:S\rar S$ is continuous, then $P:C_0(S)\rar C_0(S)$, $f\mapsto f\circ\theta$ is a linear operator on $C_0(S)$ satisfying $\norm P=1$. By the Riesz Representation Theorem the space $M(S)$ of all finite signed Borel measures $\mu$ on $S$ is isometrically isomorphic to the dual $C_0(S)^*$ of $C_0(S)$: for any $x^*\in C_0(S)^*$ there is exactly one signed Borel measure $\mu$ such that for all $f\in C_0(S)$.
$$
x^*(f)=\int f\,d\mu
\quad\mbox{and}\quad
\norm{x^*}=|\mu|(S)=\sup\Big\{\int f\,d\mu:\norm f\leq1\Big\}~.
$$
Using this identification the dual (or adjoint) mapping $P^*:M(S)\rar M(S)$ is given by $\mu\mapsto\mu_\theta$: indeed for all $f\in C_0(S)$ we have by definition and the transformation theorem of measure theory
$$
\int f\,dP^*\mu
=\int Pf\,d\mu
=\int f\circ\theta\,d\mu
=\int f\,d\mu_\theta
\quad\mbox{i.e.}\quad
P^*\mu=\mu_\theta~.
$$
The Banach space $M(S)$ is the space of all finite signed Borel measures $\mu$ on $S$ equipped with the total variation norm: $\norm{\mu}\colon=|\mu|(S)$. If in addition $S$ is discrete, then $M(S)=\ell_1(S)$. A formally more general type of operators are so called Markov operators, which we are going to discuss in the subsequent section.
Translations on $\TT^d$
Suppose $h_1,\ldots,h_d$ and are rationally independent, i.e. for all $(n_1,\ldots,n_d)\in\Z^d\sm\{0\}$:
$$
\sum n_jh_j\neq0\,\modul(1)
\quad\mbox{or equivalently}\quad
\la n,h\ra\colon=\sum n_jh_j\notin\Z,
$$
Denote by $\theta:\TT^d\rar\TT^d$ the mapping
$$
(x_1,\ldots,x_d)\mapsto(x_1+2\pi h_1,\ldots,x_d+2\pi h_d)=x+2\pi h~.
$$
Then $\theta$ is ergodic. Conversely, if $\theta$ is ergodic, then $h_1,\ldots,h_d$ and are rationally independent.
$\proof$
We remember that the functions $e_n:x\mapsto\exp(i\la n,x\ra)$, $n\in\Z^d$, form an orthonormal basis of $L_2(\TT^d)$. Hence for all $f\in L_2(\TT^d)$:
$$
f=\sum_n c_ne_n
\quad\mbox{where}\quad
c_n\colon=\la f,e_n\ra
=\frac1{(2\pi)^d}\int_0^{2\pi}\ldots\int_0^{2\pi}
f(t)e^{-i\la n,t\ra}\,dt_1\cdots dt_d~.
$$
If $f$ is not constant and $\theta$-invariant, i.e. $f=f\circ\theta$, then for all $n\in\Z^d$ satisfying $c_n\neq0$: $\exp(2\pi i\la n,h\ra)=1$, i.e. $\la n,h\ra\in\Z$. Since $f$ is not constant, there must be such an $n\in\Z^d\sm\{0\}$ and therefore $h$ must be rationally dependent. Conversely, if $h$ is rationally dependent, then there is some $n\in\Z^d\sm\{0\}$, such that $\la n,z\ra\in\Z$. If follows that $e_n$ is $\theta$-invariant.
$\eofproof$