Transformations on Manifolds
Piece-wise monotone transformations
A measurable transformation $\theta:[0,1)\rar[0,1)$ is said to be piece-wise monotone, if there is an at most countable set of pair-wise disjoint open intervals $I_k\sbe[0,1)$ such that:- $[0,1)\sm\bigcup I_k$ is a set of Lebesgue-measure $0$.
- $\theta|I_k$ is a strictly monotone $C^2$-function.
- For all $k$: $\theta(I_k)=(0,1)$.
Put $a_k(x)\colon=[1/\theta^{k-1}(x)]$ - cf. exam. Then for almost all $x\in(0,1)$ the frequency of the number $a$ in the continued fraction $a_k(x)$, $k\in\N$, of $x$ is given by
$$
\lim_{n\to\infty}\frac{|\{k\leq n: a_k(x)=a\}|}n
=\frac1{\log2}\log\Big(1+\frac1{a^2+2a}\Big)~.
$$
For large values of $a$ this is approximately $1/a^2$.
$\proof$
Since $a_k(x)=a_1(\theta^{k-1}(x))$ and $a_1(x)=a$ iff $x\in(1/(a+1),1/a)$ we conclude by Birkhoff's Ergodic Theorem:
$$
\lim_{n\to\infty}\frac{|\{k\leq n: a_k(x)=a\}}n
=\lim_{n\to\infty}\frac1n\sum_{k=1}^nI_{[a_1=a]}(\theta^k(x))
=\frac1{\log2}\int_{1/(a+1)}^{1/a}\frac1{1+x}\,dx
$$
$\proof$
Put $f(x)=\log a_1(x)$, i.e. $f|I_k=\log k$. By Birkhoff's Ergodic Theorem we get:
\begin{eqnarray*}
\lim_n\frac1n\sum_{k=1}^n\log a_k(x)
&=&\lim_n\frac1n\sum_{k=0}^{n-1}\log a_1(\theta^k(x))\\
&=&\frac1{\log2}\int_0^1\frac{f(x)}{1+x}\,dx
=\frac1{\log2}\sum_{k=1}^\infty\int_{I_k}\frac{\log k}{1+x}\,dx\\
&=&\sum_{k=1}^\infty\frac{\log k}{\log 2}\log\Big(\frac{1+1/k}{1+1/(k+1)}\Big)
=\sum_{k=1}^\infty\frac{\log k}{\log 2}\log\Big(1+\frac1{k^2+2k}\Big)~.
\end{eqnarray*}
Of course this is just the mean value of the function $x\mapsto\log a_1(x)$ with respect to the distribution given in corollary.
$\eofproof$
Transformations on Manifolds
Suppose $U,V$ are open subsets of a metric space such that $V\cap\cl U\neq\emptyset$. Then $U\cap V\neq\emptyset$. Suggested solution.
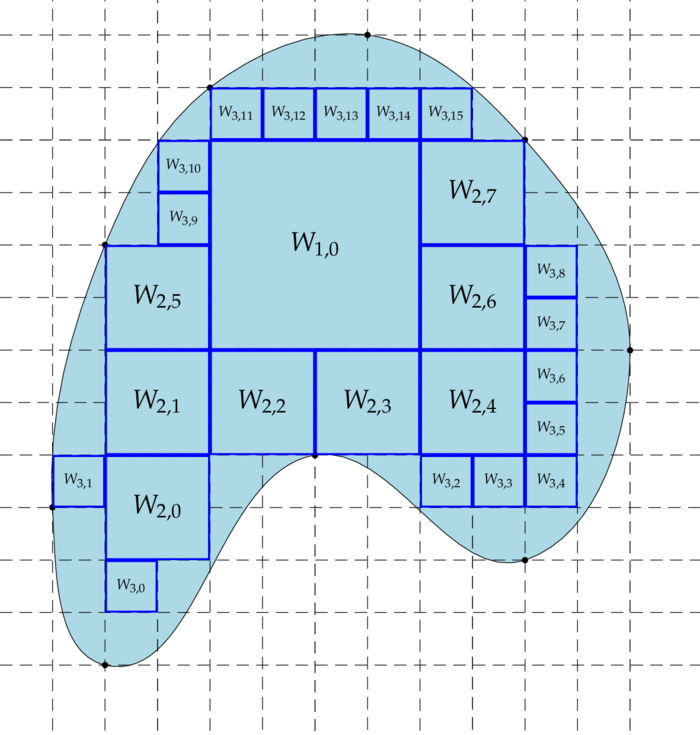
In this section we generalize the type of transformations of the previous section! Let $(S,d)$ be a Polish space, $\mu$ a $\s$-finite Borel measure on $S$ and ${\cal P}_n$, $n\in\N_0$, a sequence of collections of countably many subsets of $S$, which satisfies the following conditions:
- ${\cal P}_0=\{S\}$ and for all $W\in{\cal P}_1$: $0 < \mu(W) < \infty$.
- For all $n\in\N_0$ all sets in ${\cal P}_n$ are open and pairwise disjoint.
- For all $n\in\N_0$: $\{\cl{W}:W\in{\cal P}_n\}$ is a cover of $S$.
- For all $n\in\N_0$ and all $W\in{\cal P}_n$: $\mu(\pa W)=0$.
- For every $n\in\N_0$ all $W\in{\cal P}_{n+1}$ and all $V\in{\cal P}_n$: $W\cap V=\emptyset$ or $W\sbe V$.
- Put $d_n\colon=\sup\{d(W):W\in{\cal P}_n\}$, then $d_n\dar 0$.
Put $\F_n\colon=\s({\cal P}_n)$ and assume $\mu(S)=1$. Then for all $f\in L_1(\mu)$:
$$
\E(f|\F_n)=\sum_{W\in{\cal P}_n}\frac1{\mu(W)}\int_W f\,d\mu~.
$$
$\E(f|\F_n)$ is a martingale and the following lemma proves that it converges both in $L_1(\mu)$ and $\mu$-almost certainly to $f$ as $n\to\infty$ - cf. theorem and corollary.
$\proof$
W.l.o.g. we may assume that $\mu$ is a probability measure and $d(S)\leq1$. Put for any open subset $U$ of $S$: $J_0\colon=\{k:\cl W_{0,k}\sbe U\}$ and
$$
J_{n+1}\colon=\Big\{k:\cl W_{n+1,k}\sbe
U\sm\bigcup_{m=0}^n\bigcup_{j\in J_m}\cl W_{mj}\Big\}~.
$$
A measure $\mu(dx)=\r(x)\,v(dx)$ is $\theta$ invariant if and only if
$$
\forall x\in M:\quad
\sum_{y:\theta(y)=x}\frac{\r(y)}{|\det T_y\theta|}=\r(x)~.
$$
The linear operator that sends a function $f:M\rar\R$ to the function
$$
Tf(x)\colon=\sum_{y:\theta(y)=x}\frac{f(y)}{|\det T_y\theta|}
$$
is called the transfer operator, cf. e.g. wikipedia. If $f$ is the density of a measure $\mu$ with respect to $v$, the $Tf$ is the density of the image measure $\mu_\theta$.
Put $\theta_k:M_k\rar M$, then by the transformation rule and the change of variables formula:
\begin{eqnarray*}
\int_M f\circ\theta\,d\mu
&=&\sum_k\int_{M_k}f\circ\theta\r(\theta_k^{-1}\circ\theta)\,dv
=\sum_k\int_{M}f \r(\theta_k^{-1})\,dv_\theta\\
&=&\sum_k\int_{M}f \r(\theta_k^{-1})|\det T\theta_k^{-1}|\,dv
=\sum_k\int_{M}f \r(\theta_k^{-1})|\det T\theta_k^{-1}|/\r\,d\mu
\end{eqnarray*}
i.e. $\mu$ is $\theta$ invariant iff
$$
\sum_k\r(\theta_k^{-1}(x))|\det T_x\theta_k^{-1}|=\r(x)
$$
Since $\det T_x\theta_k^{-1}=1/\det T_{\theta^{-1}(x)}\theta_k$, the formula follows.
$\proof$
Put $f=d\nu_1/d\nu_2$ and for $n\in\N_0$: $v_n(A)\colon=v(\theta^n\in A)$, $f_n=dv_n/d\nu_2$ and
$$
g_n\colon=\frac1n\sum_{j=0}^{n-1}f_n~.
$$
Then by assumption: $f\leq g_n\leq1$. Hence by the Banach-Alaoglu Theorem the sequence $g_n$ has a weak * accumulation point $g$ in $L_\infty(\nu_2)$ satisfying: $f\leq g\leq1$. Put $d\mu\colon=g\,d\nu_2$, then by the proof of proposition: $\mu$ is $\theta$ invariant.
$\eofproof$
Let us compute for any Borel set $A$ the measure $v(\theta\in A)$: Put $B_j\colon=[\theta\in A]\cap M_j$, then
\begin{equation}\tag{TRM1}\label{trmeq1}
v(B)
=v(\theta(B_j))
=\int_{B_j}|\det T_x\theta|\,dv
=\int_{B_j}F\,dv,
\end{equation}
where $F(x)\colon=|\det T_x\theta|$. In the particular case $A=M$ we have $v(M)=1$; it follows that:
$$
\inf\{F(x):x\in M_j\}\leq\frac1{v(M_j)}\leq\sup\{F(x):x\in M_j\}~.
$$
Putting
$$
C\colon=\frac{\sup\{F(x):x\in M_j\}}{\inf\{F(x):x\in M_j\}},
$$
we get for all $x\in M_j$:
$$
F(x)
\leq\sup\{F(y):y\in M_j\}
\leq C\inf\{F(y):y\in M_j\}
\leq\frac C{v(M_j)}
$$
and analogously $F(x)\geq\frac{C^{-1}}{v(M_j)}$. Now it follows from \eqref{trmeq1} that
$$
\frac{C^{-1}}{v(M_j)}v(B_j)\leq v(B)\leq\frac C{v(M_j)}v(B_j)
$$
i.e.
\begin{equation}\tag{TRM2}\label{trmeq2}
C^{-1}v(A)v(M_j)\leq v(B_j)\leq Cv(A)v(M_j)~.
\end{equation}
Summing over $j$ proves that we conclude that for all Borel subsets $A$ of $M$:
$$
C^{-1}v(A)\leq v(\theta\in A)\leq Cv(A)~.
$$
Replacing $\theta$ with $\theta^k$ and defining $F_k(x)\colon=|\det T_x\theta^k|$ the same computation yields by lemma:
$\proof$
We only have to verify exactness of $\theta$: So suppose there is $B\in\F^T$ such that $0 < \mu(B) < 1$, i.e. $0 < v(B) < 1$. By definition of $\F^T$ we can find for every $k\in\N$ a subset $A_k\in\B$, such that $B=[\theta^k\in A_k]$. By the preceding calculations (cf. \eqref{trmeq2}) and the facts that $\mu$ is $\theta$-invariant and $C^{-1}v\leq\mu\leq Cv$ we have
\begin{eqnarray*}
v(B\cap M_{j_1,\ldots,j_k})
&=&v([\theta^k\in A_k]\cap M_{j_1,\ldots,j_k})
\geq C^{-1}v(A_k)v(M_{j_1,\ldots,j_k})\\
&\geq& C^{-2}\mu(A_k)v(M_{j_1,\ldots,j_k})
=C^{-2}\mu(B)v(M_{j_1,\ldots,j_k})
\geq C^{-3}v(B)v(M_{j_1,\ldots,j_k})~.
\end{eqnarray*}
Let $\F_k$ denote the $\s$-algebra generated by ${\cal P}_k$, then this simply says that $v(B|\F_k)\geq C^{-3}v(B)$. On the other hand by lemma and corollary the sequence $v(B|\F_k)$ converges in $L_1(v)$ to $I_B$. It follows that $I_B\geq C^{-3}v(B)$. But this is only possible if $v(B)\in\{0,1\}$.
$\eofproof$
However checking the hypothesis of proposition is a bit laborious. We need something easier to check. By the chain rule we have
$$
T_x\theta^{k+1}
=T_{\theta^k(x)}\theta\circ T_x\theta^{k}
$$
and thus $F_{k+1}(x)=F(\theta^k(x))F_k(x)$, i.e.
$$
F_{k+1}=F_kF(\theta^k)=F_{k-1}F(\theta^{k-1})F(\theta^k)
=\prod_{j=0}^k F(\theta^j)~.
$$
For any two points $x,y\in M_{j_1,\ldots,j_k}$ we get (employing $\log(1+u)\leq u$ for $u > -1$):
\begin{eqnarray*}
\Big|\frac{F_k(x)}{F_k(y)}\Big|
&=&\prod_{l=1}^{k}
\Big|\frac{F(\theta^{l-1}(x))}{F(\theta^{l-1}(y))}\Big|\\
&=&\exp\Big(\sum_{l=1}^{k}
\log\Big|1+\frac{F(\theta^{l-1}(x))-F(\theta^{l-1}(y))}
{F(\theta^{l-1}(y))}\Big|\Big)\\
&\leq&\exp\Big(\sum_{l=1}^{k}
\Big|\frac{F(\theta^{l-1}(x))-F(\theta^{l-1}(y))}
{F(\theta^{l-1}(y))}\Big|\Big)~.
\end{eqnarray*}
Since $x,y\in M_{j_1,\ldots,j_k}$ it follows by construction that for all $l\leq k$: $\theta^{l-1}(x),\theta^{l-1}(y)\in M_{j_l,\ldots,j_k}\sbe M_{j_l}$. By the mean value theorem we conclude that
$$
F(\theta^{l-1}(x))-F(\theta^{l-1}(y))
\leq\sup_{z\in M_{j_l,\ldots,j_k}}\tnorm{\nabla_z F}L(c_l)
$$
where $c_l$ is some curve in $M_{j_l,\ldots,j_k}$ connecting $\theta^{l-1}(x)$ and $\theta^{l-1}(y)$. Hence we have:
\begin{equation}\label{trmeq3}\tag{TRM3}
\Big|\frac{F(\theta^{l-1}(x))-F(\theta^{l-1}(y))}
{F(\theta^{l-1}(y))}\Big|
\leq\Big(\sup_{z,y\in M_{j_l,\ldots,j_k}}\frac{\tnorm{\nabla_z F}}{F(y)}\Big)
L(c_l)
\end{equation}
We need to find curves $c_1,\ldots,c_k$ in $M_{j_1,\ldots,j_k}$, $\ldots$, $M_{j_k}$, joining $x,y$, $\ldots$, $\theta^{k-1}(x),\theta^{k-1}(y)$.
Let $c=c_0$ be a curve joining $\theta^k(x),\theta^k(y)\in M$, then $c_k\colon=\theta_{j_k}^{-1}\circ c$ is a curve in $M_{j_k}$ joining $\theta^{k-1}(x),\theta^{k-1}(y)$ and $c_{k-1}\colon=\theta_{j_{k-1}}^{-1}\circ c_k$ is a curve in $M_{j_{k-1},j_k}\sbe M_{j_{k-1}}$ joining $\theta^{k-2}(x),\theta^{k-2}(y)$, etc. For all $l=1,\ldots,k$ the curve $c_l$ lies in $M_{j_l,\ldots,j_k}$ and thus
$$
L(c_{l-1})
=L(\theta\circ c_l)
=\int\norm{T_{c_l(t)}\theta(c_l^\prime(t)}\,dt
\geq\inf_{x\in M_{j_l,\ldots,j_k}}\inf_{\norm{X_x}=1}\norm{T_x\theta(X_x)}L(c_l)
$$
or equivalently:
$$
L(c_l)\leq\Big(\sup_{x\in M_{j_l,\ldots,j_k}}\sup_{\norm{X_x}=1}
\frac1{\norm{T_x\theta(X_x)}}\Big) L(c_{l-1})
$$
Plugging this in \eqref{trmeq3} yields:
\begin{equation}\label{trmeq4}\tag{TRM4}
\Big|\frac{F(\theta^{l-1}(x))-F(\theta^{l-1}(y))}
{F(\theta^{l-1}(y))}\Big|
\leq\Big(\sup_{x,y,z\in M_{j_l,\ldots,j_k}}\sup_{\norm{X_x}=1}
\frac{\tnorm{\nabla_z F}}{F(y)\norm{T_x\theta(X_x)}}\Big)
L(c_{l-1})
\end{equation}
Since $c_{l+n}=\theta^n\circ c_{l}$ we get by definition of the length of a curve:
$$
L(c_{l+n})=\int\sqrt{\theta^{n*}(g)(c_{l-1}^\prime(t),c_{l-1}^\prime(t))}\,dt
$$
where $\theta^*g$ denotes the pull back of the Riemannian metric $g$ by $\theta$, i.e. for all $X,Y\in T_xM$:
$$
\theta^*g_x(X,Y)\colon=g_{\theta(x)}(T_x\theta(X),T_x\theta(Y))~.
$$
Thus if $\theta^{n*}g\geq\b^2 g$ for some $n\in\N$ and some $\b > 1$, then for $m=[k/n]+1$:
$$
\sum_{l=1}^{k}L(c_{l-1})
\leq\sum_{l=1}^{n}L(c_{l-1})(1+\b^{-1}+\cdots+\b^{-m})
\leq\frac{\b}{\b-1}\sum_{l=1}^{n}L(c_{l-1})
$$
Finally if $\theta^{*}g_x\geq \d^2 g_x$, the last sum is bounded by $(1+\d^{-1}+\cdots+\d^{-n+1})L(c)$.
Theorem is just the case of an interval and the canonical Riemannian metric: $F(x)=|\theta^\prime(x)|=\norm{T_x\theta(X_x)}$ and $\norm{\nabla_x F}=|\theta^\dprime(x)|$. Therefore we get
$$
\sup_{j\in\N}\sup_{y,z\in I_j}\frac{\tnorm{\nabla_z F}}{F(y)F(x)}=
\sup_{j\in\N}\sup_{y,z\in I_j}\frac{2/z^3}{1/x^2y^2}
=\sup_{j\in\N}\frac{2(j+1)^3}{j^4}
=16~.
$$
Let us finally remark that for the Gauss map the condition we get from \eqref{trmeq3}, i.e.
$$
\Big(\sup_{x,y,z\in M_{j}}
\frac{\tnorm{\nabla_z F}}{F(y)}\Big) < \infty
$$
is not satisfied because:
$$
\sup_{j\in\N}\sup_{y,z\in I_j}\frac{\tnorm{\nabla_z F}}{F(y)}=
\sup_{j\in\N}\frac{2(j+1)^3}{j^2}
=\infty~.
$$
That's the reason for the detour to get \eqref{trmeq4}!
Let $\{0=x_0 < x_1 <\cdots < x_{N-1} < x_N=2\pi\}$ be the ordered set $f^{-1}(f(0))$. Then $M_0\colon=(x_0,x_1)\,\modul(2\pi)$, $\ldots$, $M_{N-1}=(x_{N-1},x_N)\,\modul(2\pi)$. In this case we have $F(x)=f^\prime(x)=\norm{T_x\theta}$ and thus for all $x,y,z\in M_j$:
$$
\frac{\norm{\nabla_zF}}{F(y)\norm{T_x\theta}}
=\frac{|f^\dprime(z)|}{f^\prime(y)f^\prime(x)}
\leq K~.
$$
For $x\in[0,1)=\R/\Z$ and $p\in\{2,3,\ldots\}$ the mapping $\theta(x)\colon=px\,\modul(1)$ shifts the digits of the $p$-adic expansion of $x$ one position to the left:
$$
x=\sum_{j=0}^\infty q_jp^{-j-1},\quad
\theta(x)=\sum_{j=0}^\infty q_{j+1}p^{-j-1}~.
$$
If $\theta^j(x)\in[q/p,(q+1)/p)$ for some $q\in\{0,\ldots,p-1\}$, then $q_j=q$. Moreover, Lebesgue measure on $[0,1)$ is $\theta$-invariant and since $\theta^\prime=p > 1$ and $\theta^\dprime=0$, the mapping $\theta$ is exact, hence ergodic and we get for $f=I_{[q/p,(q+1)/p)}$ for almost all $x\in[0,1)$:
$$
\lim_{k\to\infty}\frac{|\{j:0\leq j < k, \theta^j(x)=q\}|}k
=\frac1k\sum_{j=0}^{k-1}f(\theta^j(x))
=\int_0^1f\,d\l
=\frac1p~.
$$
Hence the occurrence of any digit $q$ in the $p$-adic expansion of $x$ is equally likely for almost all $x\in[0,1)$.
Homomorphisms on $\TT^d$
In proposition we found criteria for the ergodicity of translations on the torus. Here we are studying homomorphisms on the torus; for instance the mapping $\theta$ in the last example is up to the period a homomorphism $\theta:\TT\rar\TT$. For $n\in\Z^d$ let $e_n$ be the homomorphism $x\mapsto e^{i(n|x)}$ from $\TT^d$ in $S^1$ - $(.|.)$ denotes the canonical euclidean product in $\R^d$. We remark that any continuous homomorphism $\vp:\TT^d\rar S^1$ is of this type! Now suppose $u:\TT^d\rar\TT^d$ is a continuous homomorphism, then for all $n\in\Z^d$ the mapping $e_n\circ u$ is a homomorphism from $\TT^d$ into $S^1$. Hence there is exactly one $m\in\Z^d$, such that $e_n\circ u=e_m$. The mapping $u^*:\Z^d\rar\Z^d$, $n\mapsto m$ is called the adjoint of the homomorphism $u$ (in analogy to the adjoint $u^*:F^*\rar E^*$ of a homomorphism $u:E\rar F$ of vector-spaces $E$ and $F$). Let us write $\la x,n\ra\colon=e_n(x)$, then $u^*$ is defined by $$ \forall x\in\TT^d\,\forall n\in\Z^d:\quad \la u(x),n\ra =\la x,u^*(n)\ra~. $$ Since $$ \la x,u^*(n+m)\ra =\la u(x),n+m\ra =\la u(x),n\ra\la u(x),m\ra =\la x,u^*(n)\ra\la x,u^*(m)\ra =\la x,u^*(n)+u^*(m)\ra, $$ the mapping $u^*:\Z^d\rar\Z^d$ is a homomorphism as well. If $v:\TT^d\rar\TT^d$ is another homomorphism, then $$ \la uv(x),n\ra =\la v(x),u^*(n)\ra =\la x,v^*u^*(n)\ra \quad\mbox{i.e.}\quad (uv)^*=v^*u^*~. $$ Is the normalized Haar measure $\l$ on $\TT^d$ $u$-invariant? First of all we get for all $n\in\Z^d\sm\{0\}$: $$ \int\la u(x),n\ra\,\l(dx) =\int\la x,u^*(n)\ra\,\l(dx) $$ and this vanishes iff $u^*(n)\neq0$. Hence the measure $\l$ cannot be $u$ invariant unless $u^*$ is injective. On the other hand if $u^*$ is injective, then for all $f\in L_2(\TT^d)$: $f=\sum c_ne_n$ and $$ \int f\circ u\,d\l =\sum\int c_ne_n\circ u\,d\l =\sum\int c_n\la n,u\ra\,d\l =\sum\int c_n\la u^*(n),x\ra\,\l(dx) =c_0 =\int f(x)\,d\l(dx) $$ Hence $\l$ is $u$ invariant iff $u^*$ is injective! $\proof$ If $\{u^{k*}(n):\,k\in\N\}$ is finite for some $n\in\Z^d\sm\{0\}$, then there is a minimal $k\in\N$, such that $u^{*k}(n)=n$. In this case $$ f(x)\colon=\sum_{j=0}^{k-1}\la x,u^{*j}(n)\ra $$ is $u$ invariant and not constant. Conversely define for any pair of finite sets $N\sbe\Z^d\sm\{0\}$ and $M\sbe\Z^d$: $$ f(x)=\sum_{n\in N}a_n\la x,n\ra,\quad g(x)=\sum_{m\in M}b_m\la x,m\ra. $$ Then $$ \int f\circ u^k\bar g\,d\l =\sum_{n,m}a_n\bar b_m\int\la x,u^{k*}n\ra\cl{\la x,m\ra}\,\l(dx) $$ Now $\int\la x,u^{k*}(n)\ra\cl{\la x,m\ra}\,\l(dx)\neq0$ if and only if $u^{k*}(n)=m$. We claim that for sufficiently large $k\in\N$: $u^{k*}(N)\cap M=\emptyset$. Otherwise we could find $n\in N$ and $m\in M$ such that $u^{k*}(n)=m$ for infinitely many $k\in\N$ and this in turn would imply that $\{u^{k*}(n):k\in\N\}$ is finite. Hence for sufficiently large $k\in\N$: $\int f\circ u^k\bar g\,d\l=0$. But these functions $f$ form a dense subset of the orthogonal complement $E$ of the constant functions in $L_2(\TT^d)$ and thus for all $f\in E$ and all $g\in L_2(\TT^d)$: $$ \lim_k\int f\circ u^k\bar g\,d\l=0~. $$ $\eofproof$
For all $p\in\Z\sm\{-1,0,1\}$ the mapping $x\mapsto px\,\modul(2\pi)$ is mixing, i.e.for all $f,g\in L_2(\TT)$:
$$
\lim_{k\to\infty}\int g(p^kx)f(x)\,\l(dx)=\int g\,d\l\cdot\int f\,d\l~.
$$
This is a particular case of the Fejer lemma, which states that for all $1\leq r < \infty$, all $g\in L_r(\TT)$ and all $f\in L_q(\TT)$, $1/r+1/q=1$: $\lim_{k\to\infty}\int g(kx)f(x)\,\l(dx)=\int f\,d\l\cdot\int g\,d\l$. For trigonometric polynomials $g$ this is the well known Riemann-Lebesgue lemma and for $g\in L_r(\TT)$ the result follows by a density argument (compare lemma).
Obviously $u^*(n)=pn$ and $u^{*k}(n)=p^kn$. Hence for all $n\in\Z\sm\{0\}$ all points in the set $\{u^{*k}(n):k\in\N\}$ are different.
$\proof$
If $u^{*k}(n)=n$ for some $n\in\Z^d\sm\{0\}$, then the set $\{u^{*l}(n):\,l\in\N\}$ contains at most $k$ points. Conversely if this set is finite for some $n\in\Z^d\sm\{0\}$, then there are natural numbers $m < l$ such that $u^{*m}(n)=u^{*l}(n)$. As $u^*$ is an isomorphism this holds if and only if $u^{*l-m}(n)=n$.
$\eofproof$
In fact it can be shown (cf. e.g. exam) that $u^*$ is an isomorphism iff $u$ is an isomorphism.
$\proof$
$u_A$ is well defined iff for all $n\in\Z^d$: $u_A(x+2\pi n)=u_A(x)$, which holds if and only if $A(\Z^d)\sbe\Z^d$. Put $u=u_A$, then
\begin{eqnarray*}
\la x,u^*(1,0,\ldots,0)\ra
&=&\la u(x),(1,0,\ldots,0)\ra
=\la(\sum_la_{1l}x_l,\ldots,\sum_la_{dl}x_l),(1,0,\ldots,0)\ra\\
&=&\exp(i\sum_la_{1l}x_l)
=\prod_{l=1}^d\exp(ia_{1l}x_l)
=\la x,(a_{11},\ldots,a_{1d})\ra~.
\end{eqnarray*}
Analogously we get $u^*(0,\ldots,1,0,\ldots,0)=(a_{j1},\ldots,a_{jd})$, where $1$ is in slot $j$. Hence $u^*(n)=A^t(n_1,\ldots,n_d)^t$ and $u_A$ is mixing iff $1$ is not an eigen-values of $A^{kt}$. Now, for any matrix $B\in\Ma(n,\R)$ $B$ and $B^t$ have the same characteristic polynomial and thus both matrices have the same eigen-values. Hence $u_A$ is mixing iff for all $k\in\N$ $1$ is not an eigen values of $A^k$. Finally, if $1$ is an eigen-value of $A^k$, then
$$
\{0\}\neq
\ker(A^k-1)
=\ker(A-e_1)\cdots(A-e_k)
=\ker(A-e_1)\oplus\cdots\oplus\ker(A-e_k)
$$
where $e_j\colon=e^{2\pi i(j-1)/k}$. This holds because the complex numbers $e_1,\ldots,e_k$ are all mutually different and we have the following result from linear algebra: Suppose $p,q$ are polynomials such that $\gcd(p,q)=1$. Then for any vector space $E$ and any $A\in\Hom(E)$ we have:
$$
\ker(p(A)q(A))=\ker(p(A))\oplus\ker(q(A))~.
$$
$\eofproof$
Since $\det A=\pm1$ the eigen-values of $A$ are $z$ and $\pm1/z$. Thus $z=e^{2\pi i/k}$ implies: $\tr A=z\pm1/z=2\cos(2\pi/k)$ or $\tr A=2i\sin(2\pi/k)$. Now $\tr A\in\Z$ and therefore this can only happen if $2\cos(2\pi/k)\in\{-2,-1,0,1,2\}$ or $\sin(2\pi/k)=0$, i.e. $k\in\{1,2,3,4,6\}$ and $|\tr A|\leq2$.
Billiards
A point-like particle moves freely inside a bounded domain $D$ (i.e. $D$ is open and connected) with piece-wise smooth boundary $M\colon=\pa D$. Only in case it hits the boundary it gets reflected according to the laws of elastic collision. So assume that there is a unit outward vector-field $N$ to $M$, the particle moves with unit momentum and it hits the boundary in $x$. If $u\in T_x\R^d$, $\Vert u\Vert=1$, is the momentum before collision, then $$ v=u-2\la u,N\ra N $$ is its momentum after collision. Denoting by $y$ the following point of reflection (the first point of intersection of the half-line $t\mapsto x+tv$, $t > 0$, and the boundary $M$), the transformation $\theta:(x,u)\mapsto(y,v)$ defines a map $\theta:M\times S^{d-1}\rar M\times S^{d-1}$.
If $D$ is the unit circle in $\R^2$, then $\theta(z,u)=-(z^3u^{-2},z^2u^{-1})$, where $M=S^1$ is considered as a subset of the complex plane $\C$. Prove that the Haar measure on $S^1\times S^1$ is $\theta$ invariant and that $\theta$ is not ergodic. Suggested solution.
Hyperbolic transformations
A smooth diffeomorphism $\theta:M\rar M$ on a Riemannian manifold $M$ is said to be hyperbolic (cf. e.g. wikipedia) if the tangent bundle $TM=T^sM\oplus T^uM$ can be split into two sub-bundles invariant under the tangent map $T\theta$ and if there exists constants $c,K > 0$, such that for all $n\in\N$ and all $x\in M$: $$ \norm{T_x\theta^n:T_x^sM\rar T_{\theta^n(x)}^sM}\leq Ke^{-cn} \quad\mbox{and}\quad \norm{T_x^{-1}\theta^n:T_{\theta^n(x)}^uM\rar T_x^uM}\leq Ke^{-cn} $$ Analogously the flow $\theta_t$ of a vector field $X$ is said to be hyperbolic if for all $t > 0$ and all $x\in M$: $$ \norm{T_x\theta_t:T_x^sM\rar T_{\theta_t(x)}^sM}\leq Ke^{-ct} \quad\mbox{and}\quad \norm{T_x^{-1}\theta_t:T_{\theta_t(x)}^uM\rar T_x^uM}\leq Ke^{-ct}~. $$ This is some sort of generalization of exam: A smooth diffeomorphism $\theta:\TT^d\rar\TT^d$ is hyperbolic if there exists some number $L\in(0,1)$ such that for each $x\in\TT^d$ we have a splitting $\R^d=E_x\oplus F_x$ of the euclidean space $\R^d$ satisfying $$ \norm{D\theta(x):E_x\rar E_{\theta(x)}}\leq L \quad\mbox{and}\quad \norm{D\theta(x):F_x\rar F_{\theta(x)}}\geq L^{-1}~. $$ Though baker's transformation is not smooth it's a typical example of an hyperbolic transformation. Anyhow baker's transformation is ergodic in $L_1([0,1)^2)$.Return and Hitting Times
Kac's return time formula
Informally speaking Poincaré's Theorem asserts that starting in $x\in A$ there is a good chance for the sequence $\theta^n(x)$, $n\in\N$, to return infinitely many times to $A$. Kac's formula is about the expected value of the first time of return to $A$.Suppose we have an ergodic dynamical system $(S,\F,\mu,\theta)$, $\mu(S)=1$, and a subset $A\in\F$ such that $\mu(A) > 0$. Then the set $\bigcup_n[\theta^n\in A]$ is invariant and it's measure is greater than $\mu(A)$. By ergodicity it must have measure $1$ and thus for $\mu$ almost all $x\in S$ the first return time $$ T\colon=T_A\colon=\inf\{n\in\N:\theta^n(x)\in A\} $$ is $\mu$-a.e. finite. Moreover as $$ [T < n]=\bigcup_{k=1}^{n-1}[\theta^k\in A] $$ the map $T$ is measurable. If $I_AT$ is integrable, then by Birkhoff's Ergodic Theorem we have for $\mu$ almost all $x\in S$: $$ \int_A T\,d\mu=\lim_{n\to\infty}\frac1n\sum_{k=0}^{n-1}(I_AT)(\theta^k(x))~. $$ The idea for the calculation of the right hand side is to take instead of $n\in\N$ the sequence $T^j(x)$, $j\in\N$, of $j$-th return times: $$ T^1\colon=T \quad\mbox{and for $j > 1$:}\quad T^j(x)\colon=\inf\{n > T^{j-1}(x): \theta^n(x)\in A\}~. $$ Put for $x\in A$: $\theta_A(x)\colon=\theta^{T(x)}(x)\in A$, then $\theta_A$ is a transformation on $A$ and $\theta_A^j(x)$ is the $j$-th return point in $A$. Hence $$ T^{j+1}(x)=T(\theta_A^j(x))+T^j(x) $$ and by iteration it follows that \begin{equation}\label{rhteq1}\tag{RHT1} T^{j+1}=\sum_{k=0}^{j}T\circ\theta_A^k~. \end{equation} Now $(I_AT)(\theta^k(x))$ equals $0$ if $\theta^k(x)\notin A$ and it equals $T(\theta^k(x))$ if $\theta^k(x)\in A$; up to time $T^j(x)-1$ the latter happens exactly $j-1$ times, i.e. $$ \sum_{k=0}^{T^j(x)-1}(I_AT)(\theta^k(x))=\sum_{k=0}^{j-1}T(\theta_A^k(x))~. $$ Thus by \eqref{rhteq1}: $$ \lim_{j\to\infty}\frac1{T^j(x)}\sum_{k=0}^{T^j(x)-1}(I_AT)(\theta^k(x)) =\lim_{j\to\infty}\frac1{T^j(x)}\sum_{k=0}^{j-1}T(\theta_A^k(x)) =\lim_{j\to\infty}\frac1{T^j(x)}T^j(x)=1~. $$ To prove that $I_AT$ is integrable apply the previous arguments to the truncated integrable function $I_{A\cap[T < C]}T$ for any $C > 0$.
If $\theta$ is an ergodic transformation on the probability space $(S,\F,\mu)$, then for all $A\in\F$ satisfying $\mu(A) > 0$:
$$
\int_A T_A\,d\mu=1,
$$
where $T_A\colon=\inf\{n\in\N:\theta^n(x)\in A\}$ is the first return time.
By subsection the shift operator $\Theta$ is ergodic on $(\O,\F^X,\P^\mu)$. For every $n$ we have $X_0\circ\Theta_n=X_n$ and thus we get for $B\colon=[X_0\in A]$:
$$
T_B
=\inf\{n:\Theta_n\in B\}
=\inf\{n:X_0\circ\Theta_n\in A\}
=\inf\{n:X_n\in A\}
=T_A~.
$$
Hence $\E^\mu(T_A;X_0\in A)=\E^\mu(T_B;B)=1$.
If $X_n$ is the random walk on a finite undirected and connected graph $G=(V,E)$ (cf. exam), then
$$
\forall x\in V:\quad
\E^x T_x=\frac{2|E|}{d(x)},
\quad\mbox{where}\quad
T_x\colon=T_{\{x\}}.
$$
By exam the measure $\mu(x)\colon=d(x)/2|E|$ is the reversible probability measure and by exam we have for all $x\in V$:
$$
1=\E^\mu(T_x;X_0=x)
=\sum_y\E^y(T_x;X_0=x)\mu(y)
=\E^xT_x\mu(x)
$$
For the Markov chain given in exam we have for all Borel sets $A$ in $S$, all $x\in S$ and all $n\in\N$: $\P^x(T_A=n)=\P^\mu(T_A=n)=\mu(A)(1-\mu(A))^{n-1}$. 2. Show that for all $t < -\log(1-\mu(A))\sim\mu(A)$: $\E^\mu e^{tT_A} < \infty$ and compute its value.
Hitting times
Let $X_n$ be a Markov chain in $S$. For any set $A\sbe S$ the random variable
$$
H_A\colon=\inf\{n\geq0:X_n\in A\}
$$
is called the hitting time of $A$. Prove that $f(x)\colon=\E^xH_A$ solves for all $x\notin A$ the equation $f(x)=1+Pf(x)$, i.e. $Lf(x)=-1$. 2. Verify that in case $X_n$ is the simple random walk on $\Z_{2p}=\{-(p-1),\ldots,-1,0,1,\ldots,p-1,p\}$ and $A=\{p\}$: $f(x)=p^2-x^2$.
1. On the set $[H_A\geq1]$ we have: $H_A\circ\Theta=\inf\{n\geq0:X_{n+1}\in A\}=H_A-1$. Since $[H_A\geq1]=[X_0\notin A]\in\F_0\sbe\F_1$ we infer from the extended Markov property:
\begin{eqnarray*}
f(x)
&=&\E^x(H_A;H_A\geq1)\\
&=&\E^x(\E^x(1+H_A\circ\Theta|\F_1);H_A\geq1)\\
&=&\P^x(H_A\geq1)+\E^x(\E^{X_1}H_A;H_A\geq1)\\
&=&\P^x(X_0\notin A)+\E^x(f(X_1);H_A\geq1)~.
\end{eqnarray*}
If $x\notin A$, then the right hand side equals $1+Pf(x)$. If $x\in A$ then both sides vanish!2. In this case $Lf(x)=\tfrac12(f(x+1)-2f(x)+f(x-1))$ and for all $x\neq p$: $f(x+1)-2f(x)+f(x-1)=-2$ and $f(p)=0$. The general solution of this difference equation is $f(x)\colon=-x^2+ax+b$. By symmetry we conclude that: $a=0$ and since $f(p)=0$ we finally get: $f(x)=p^2-x^2$.
Let $X_n$ be the simple random walk on $\Z_2^3$, $A=\{(1,1,1)\}$. Compute for all $x\in\Z_2^n$: $\E^xH_A$. Suggested solution.
For a general stochastic matrix $P$ there is an easy procedure to compute $f(x)\colon=\E^xH_A$ for any subset $A\sbe S$: Since we know that $f(x)=0$ for all $x\in A$, we delete from $P$ all rows $x$ and columns $y$, where $x,y\in A$, to get a so called sub-Markovian matrix $Q$ with $|A^c|$ rows and columns. Now solve the linear equation $(1-Q)f=c$, where $c$ is the constant function $1$. In sage the above example can be solved as follows:
P=matrix(QQ,[[0,1,1,1,0,0,0,0],[1,0,0,0,1,0,1,0],[1,0,0,0,0,1,1,0],[1,0,0,0,1,1,0,0],[0,1,0,1,0,0,0,1],[0,0,1,1,0,0,0,1],[0,1,1,0,0,0,0,1],[0,0,0,0,1,1,1,0]])
P=(1/3)*P
I=identity_matrix(7)
c=vector(QQ,[1,1,1,1,1,1,1])
Q=P.matrix_from_columns([0,1,2,3,4,5,6])
Q=Q.matrix_from_rows([0,1,2,3,4,5,6])
L=I-Q
L.solve_right(c)
Here is an alternative approach via martingales: By exam we know that for each bounded measurable $f:S\rar\R$
$$
M_n^f\colon=f(X_n)-f(X_0)-\sum_{j=0}^{n-1}Lf(X_j)
$$
is a martingale with respect to all $\P^x$. Hence if $-Lf=g$ (and bounded $f,g$) then by the Optional Stopping Theorem for all stopping times $N$: $\E^xM_N^f=\E^xM_0^f$, i.e.
$$
f(x)=\E^xf(X_N)+\E^x\sum_{j=0}^{N-1}g(X_j)~.
$$
Now suppose $f|A=0$, then $f(X_{H_A})=0$ and
$$
f(x)=\E^x\Big(\sum_{j=0}^{H_A-1}g(X_j)\Big)~.
$$
Formally, our first approach shows that the function $f(x)\colon=\E^xH_A$ solves the equation $Lf=-1$, $f|A=0$ and our second approach shows that if $f$ solves the equation $Lf=-1$, $f|A=0$, then - under certain integrability conditions, which we don't care: $f(x)=\E^xH_A$.P=(1/3)*P
I=identity_matrix(7)
c=vector(QQ,[1,1,1,1,1,1,1])
Q=P.matrix_from_columns([0,1,2,3,4,5,6])
Q=Q.matrix_from_rows([0,1,2,3,4,5,6])
L=I-Q
L.solve_right(c)
Remark: If $B_t$ is a diffusion on a manifold $M$ with generator $f\mapsto-(\D f+X)f$ and $A$ is a subset with smooth boundary, then the function $f(x)\colon=\E^x H_A$ is the solution of the PDE (cf. e.g. R. Durrett, Brownian Motion and Martingales in Analysis): $$ (\D+X)f=1\quad\mbox{on $A^c$ and}\quad f|\pa A=0~. $$ In particular for the Brownian motion on the torus $\TT$ and $A=\{\pi\}$: $-\tfrac12\pa_\theta^2f=1$ and $f(\pm\pi)=0$, i.e. $f(\theta)=\pi^2-\theta^2$ - compare exam 2.!
Similarly we can find the distribution $u_n(x)\colon=\P^x(H_A=n)$. We obviously have $u_0=I_A$ and thus $PI_A(x)=\P^x(X_1\in A)=\P^x(H_A=1)$. Actually, the same argument as above shows that for all $x\notin A$: $u_n(x)=Pu_{n-1}(x)$, i.e. for all $x\in S$ and all $n\geq1$: $u_{n+1}(x)=I_{A^c}(x)Pu_n(x)=\colon Qu_n(x)$. \begin{equation}\label{rhteq2}\tag{RHT2} u_{n+1}(x) =Q^nu_1(x)~. \end{equation} Thus we define $$ Q(x,B)\colon=\left\{\begin{array}{cl} P(x,B\cap A^c)&\mbox{if $x\in A^c$}\\ 0&\mbox{otherwise} \end{array}\right. $$ and get for all bounded, measurable functions $f:S\rar\R$: $Qf(x)\colon=\int f(y)\,Q(x,dy)$ and $Qf|A=0$. $Q$ is just the same sub-Markovian operator as above. Alternatively we may define another Markov operator $R$ which has $A$ as an absorbing set, i.e. $$ R(x,B)\colon=\left\{\begin{array}{cl} P(x,B)&\mbox{if $x\in A^c$}\\ \d_x(B)&\mbox{if $x\in A$} \end{array}\right. $$ Once the Markov chain hits $A$ it gets stuck there! If $P$ is a stochastic matrix this gives another stochastic matrix $R$ by replacing all rows of $P$ corresponding to points $x\in A$ with rows having entry $1$ in the diagonal positions $(x,x)$ and zeros in all other positions. In case of exam the stochastic matrix $R$ is given by $$ \begin{array}{cccccccc} 0&0&1/3&1/3&0&0&0&0\\ 1/3&0&0&0&1/3&0&1/3&0\\ 1/3&0&0&0&0&1/3&1/3&0\\ 1/3&0&0&0&1/3&1/3&0&0\\ 0&1/3&0&1/3&0&0&0&1/3\\ 0&0&1/3&1/3&0&0&0&1/3\\ 0&1/3&1/3&0&0&0&0&1/3\\ 0&0&0&0&0&0&0&1 \end{array} $$ For a random walk $X_n$ on a graph this gives another random walk $Y_n$, that gets stuck once it has jumped into $A$, i.e. for all $x\in A$ and all $n\in\N$: $\P^x(Y_n=x)=1$ (or $\P^x(Y_n\neq x)=0$).
Given the adjacency matrix of an undirected finite graph $G=(E,V)$, two points $x\neq y\in E$ and $n\in\N$. Write a program to compute $\P^x(H_y=n)$, where $H_y\colon=H_{\{y\}}$. C code, example input file and code to generate edges of the $d$ dimensional cube.
We use the labels from exam
P=matrix(QQ,[[0,1,1,1,0,0,0,0],[1,0,0,0,1,0,1,0],[1,0,0,0,0,1,1,0],[1,0,0,0,1,1,0,0],[0,1,0,1,0,0,0,1],[0,0,1,1,0,0,0,1],[0,1,1,0,0,0,0,1],[0,0,0,0,1,1,1,0]])
P=(1/3)*P
u0=vector(QQ,[0,0,0,0,0,0,0,1])
u=P*u0;u
u=vector(QQ,[0,0,0,0,1/3,1/3,1/3])
Q=P.matrix_from_columns([0,1,2,3,4,5,6])
Q=Q.matrix_from_rows([0,1,2,3,4,5,6]);Q
for i in range(22):
u=Q*u
print(N(u,digits=5))
P=(1/3)*P
u0=vector(QQ,[0,0,0,0,0,0,0,1])
u=P*u0;u
u=vector(QQ,[0,0,0,0,1/3,1/3,1/3])
Q=P.matrix_from_columns([0,1,2,3,4,5,6])
Q=Q.matrix_from_rows([0,1,2,3,4,5,6]);Q
for i in range(22):
u=Q*u
print(N(u,digits=5))
Show that the function $v_n(x)\colon=\P^x(H_A > n)$ satisfies the recursion $v_{n+1}(x)=Pv_n(x)$ for all $x\in A^c$, $v_0=I_{A^c}$ and for all $n$ and all $x\in A$: $v_n(x)=0$, i.e. $v_n=Q^nI_{A^c}$. Suggested solution.
Assume $u_{n+1}=Pu_n$, i.e. $u_{n+1}-u_n=Lu_n$, then $M_k\colon=u_{n-k}(X_k)$, $k=0,\ldots,n$ is a martingale. Suggested solution.
Remark: If $B_t$ is a diffusion on a manifold $M$ with generator $f\mapsto-(\D f+X)f$ and $A$ is a subset with smooth boundary, then the function $u(x)\colon=\P^x(H_A > t)$ is the solution of the parabolic PDE (cf. e.g. R. Durrett, Brownian Motion and Martingales in Analysis):
$$
\pa_tu=-(\D+X)u,\quad
\forall x\in A^c:\quad u(0,x)=1,\quad
\forall t > 0\,\forall x\in\pa A^c:\quad u(t,x)=0~.
$$
In particular for the Brownian motion on the torus $\TT$ and $A=\{\pi\}$: $\pa_tu=\tfrac12\pa_\theta^2u$, $u(0,\theta)=1$ and for all $t > 0$: $u(t,\pm\pi)=0$.
Solve the parabolic PDE
$$
\pa_tu=\tfrac12\pa_\theta^2u,\quad
\forall\theta\neq\pm\pi:\quad u(0,x)=1,\quad
\forall t > 0:\quad u(t,\pm\pi)=0~.
$$
by Fourier analysis methods. Suggested solution.
Suppose $X_n$ is a Markov chain in $S$, then for $t > 0$ the function $h(x)=\E^x e^{tH_A}$ (provided it exists) solves for all $x\notin A$ the equation: $Ph(x)=e^{-t}h(x)$. 2. If $X_n$ is the simple random walk on $\Z$, $A=\{x\in\Z:|x|\geq p\}$, then for all $|x| < p$: $h(x+1)+h(x-1)=2e^{-t}h(x)$ and $h(\pm p)=1$. 3. Put $\cos\vp=e^{-t}$ and $\sin\vp=(1-e^{-2t})^{1/2}$, then
$$
\forall |x| < p:\quad
h(x)=\frac{\cos(\vp x)}{\cos(\vp p)}
$$
provided that $\vp p < \pi/2$, i.e. $t < -\log\cos(\pi/2p)$. Suggested solution.
Solve the equation: $Ph(x)=e^{-t}h(x)$ and $h|A=0$, for the Markov operator $P$ of the simple random walk on the dodecahedron and $A=\{20\}$. Determine the maximal value of $t$.
Suppose $X_n$ is a Markov chain in $S$. If $h$ solves the equation $Ph=e^{-g}h$, then
$$
M_n\colon=h(X_n)\exp\Big(\sum_{j=0}^{n-1}g(X_j)\Big)
$$
is a martingale with respect to all $\P^x$. Of course, we need some integrability condition; if you like assume that both $h$ and $g$ are bounded! If moreover $h|A=1$, then (suggested solution)
$$
h(x)=\E^x\exp\Big(\sum_{j=0}^{H_A-1}g(X_j)\Big)~.
$$
Remark: If $B_t$ is a diffusion on a manifold $M$ with generator $f\mapsto-(\D f+X)f$ and $A$ is a subset with smooth boundary, then the function $h(x)\colon=\E^x e^{tH_A}$ is the solution of the PDE (cf. e.g. R. Durrett, Brownian Motion and Martingales in Analysis):
$$
(\D+X)h=th
\quad\mbox{on $A^c$ and}\quad
h|\pa A=1~.
$$
In particular for the Brownian motion on the torus $\TT$ and $A=\{\pi\}$: $-\tfrac12\pa_\theta^2h=th$ and $h(\pm\pi)=1$, i.e. (compare exam 2.)
$$
\forall t < 1/8:\quad
h(\theta)=\frac{\cos(\sqrt{2t}\,\theta)}{\cos(\sqrt{2t}\,\pi)}~.
$$
$\proof$
For all $m\geq1$ we conclude by the extended Markov property and the fact that $[H_A\geq n]\in\F_n$:
\begin{eqnarray*}
\P^x(H_A\geq(m+1)n)
&=&\P^x(H_A\geq mn,H_A\circ\Theta_{mn}\geq n)\\
&=&\E^x(\P^x(H_A\circ\Theta_{mn}\geq n|\F_{mn});H_A\geq mn)\\
&=&\E^x(\P^{X_{mn}}(H_A\geq n);H_A\geq mn)
\leq c_n\P^x(H_A\geq mn)~.
\end{eqnarray*}
The assertion follows by induction on $m$.
$\eofproof$
Consider $\Z_2$ as the set $\{\pm1\}$ with multiplication. For every $d\in\N$ and every subset $A$ of $\{1,\ldots,d\}$ put $w_A:\Z_2^d\rar\{\pm1\}$,
$$
w_A(\o)\colon=\prod_{j\in A}\o_j,\quad
w_\emptyset\colon=1~.
$$
Then $w_A$, $A\sbe\{1,\ldots,d\}$, is an orthonormal basis for $L_2(\Z_2^d)$ -the measure being the normalized counting measure. These functions $w_A$ are called the Walsh functions. 2. If $P$ denotes the Markov operator of the simple random walk on $\Z_2^d$, then
$$
Pw_A=\l_{|A|}w_A
\quad\mbox{and}\quad
\l_n=1-2\frac{n}{d}
\quad\mbox{for}\quad
n=0,\ldots,d~.
$$
In particular the multiplicity of $\l_n$ is ${d\choose n}$. Suggested solution.
Remark: Suppose $G$ is a finite group with unit $e$ and $R\sbe G\sm\{e\}$ a symmetric set of generators of $G$ such that for all $x\in G$: $xRx^{-1}\sbe R$. The Cayley graph $(G,R)$ of $G$ is a simple graph with vertex set $G$ and the edges are all pairs $(x,y)$ such that $xRy$. For every irreducible unitary representation $\Psi$ of $G$ there are sub-algebras ${\cal A}_\Psi$ of the convolution algebra $L_2(G)$ such that for any pair of in-equivalent irreducible representations $\Psi$ and $\Phi$: ${\cal A}_\Psi*{\cal A}_\Phi=\{0\}$, moreover
$$
L_2(G)=\bigoplus_{\Psi\in\wh G}{\cal A}_\Psi
$$
is an orthogonal decomposition - $\wh G$ denotes the set of all pairwise in-equivalent irreducible unitary representations of $G$. These spaces ${\cal A}_\Psi$ are eigen-spaces of the Markov operator associated to the Cayley graph (cf. e.g. Cayley Graphs). Beware: the eigen-values corresponding to these spaces are not necessarily different for different irreducible unitary representations. In case $G$ is abelian the set $\wh G$ is just the set of all characters of $G$, i.e. the set of all homomorphisms $\chi:G\rar S^1$ and the algebra ${\cal A}_\chi$ is the one dimensional space generated by the character $\chi$. For e.g. $G=\Z_2^d=\{\pm 1\}^d$ the characters are the Walsh functions!
A Markov chain with transition function $P(x,A)$ on $S$ is called a Harris chain if there are subsets $A,B\in\B(S)$, $\e\in(0,1)$ and a probability measure $\l$ on $B$ such that
- For all $x\in S$: $\P^x(T_A < \infty)=1$.
- For all $x\in A$ and all measurable $C\sbe B$: $P(x,C)\geq\e\l(C)$.
Feller Operators and Semigroups on $C_b(S)$
Feller semigroups and transition functions
Let $S$ be a Polish space and let $C_b(S)$ be the space of bounded complex valued continuous functions on $S$ endowed with the norm $\norm{f}=\sup\{|f(x)|:x\in S\}$. A continuous Feller semigroup on $C_b(S)$ (or $C_{bu}(S)$) is a continuous, positive and conservative contraction semigroup of the form $$ P_tf(x)=\int_S f(y)\,P_t(x,dy), $$ where for all $x\in S$ and all $t > 0$ $A\mapsto P_t(x,A)$ is a probability measure on $S$. The semigroup property is equivalent to \begin{equation}\label{mcseq1}\tag{MCS1} \forall x\in S\,\forall A\in\B(S):\quad P_{t+s}(x,A)=\int P_s(y,A)\,P_t(x,dy)~. \end{equation} A family $P_t(x,A)$ satisfying \eqref{mcseq1} is called a family of Markovian transition functions. It is a Feller transition function if the associated contraction semigroup $P_tf(x)\colon=\int_S f(y)\,P_t(x,dy)$ is a continuous Feller semigroup on $C_b(S)$; this means that the associated contraction semigroup $P_t$ must in addition map $C_b(S)$ into $C_b(S)$ and for all $f\in C_b(S)$ the mapping $t\mapsto P_tf$ must be a continuous curve in $C_b(S)$.
If $P_t(x,A)$ is a family of Markovian transition function on a Polish space $S$, then the associated semigroup $P_t$ is a continuous Feller semigroup on $C_b(S)$ if
1. Since $A\mapsto P_t(x,A)$ is a measure, we have for every positive, continuous function $f:S\rar[0,1]$
$$
P_tf(x)
=\int f(y)\,P_t(x,dy)
=\int_0^1 P_t(x,f > r)\,dr~.
$$
Thus if $x\mapsto P_t(x,U)$ is continuous for all open sets $U$, then $P_tf$ is continuous (by bounded convergence).- $x\mapsto P_t(x,U)$ is continuous for all open subsets $U\sbe S$.
- The family $P_t(x,A)$ is uniformly stochastically continuous, i.e. $$ \forall r > 0:\quad \lim_{t\dar0}\inf_{x\in S}P_t(x,B_r(x))=1~. $$
2. For $f\in C_b(S)$ and $\e > 0$ we choose $\d,r > 0$ such that for all $y\in B_r(x)$: $|f(y)-f(x)| < \e$ and for all $x\in S$ and all $t < \d$: $P_t(x,B_r(x)^c) < \e$. Then $$ \sup_{x\in S}|P_tf(x)-f(x)| \leq\int_{B_r(x)}|f(y)-f(x)|\,P_t(x,dy)+2\norm f \sup_{x\in S}P_t(x,B_r(x)^c)) \leq\e+2\e\norm f~. $$ Suppose $S$ is locally compact. Given $\e > 0$ and $f\in C_0(S)$ put $K\colon=[|f|\geq\e]$, then there is another compact subset $E=E(\e,t,K)$ of $S$ such that for all $x\notin E$: $P_t(x,K) < \e$. Hence for all $x\notin E$: $$ |P_tf(x)| \leq\int_K|f(y)|P_t(x,dy)+\e \leq\norm f\,P(x,K)+\e \leq(\norm f+1)\e, $$ which proves that $P_tf$ is in $C_0(S)$. The last assertion is just exam! $\eofproof$ The family of adjoints $P_t^*$ is also a semigroup, but as $C_b(S)$ is in general not reflexive (cf. theorem) it's in general not continuous. Anyhow for $\mu\in M_1(S)$ we have by definition of the adjoint for all $f\in C_b(S)$: $$ \int f\,dP_t^*\mu =\int P_tf\,d\mu =\iint f(y)\,P_t(x,dy)\,\mu(dx) \quad\mbox{i.e.}\quad P_t^*\mu(A)=\int P_t(x,A)\,\mu(dx)~. $$ In particular $P_t^*(M_1(S))\sbe M_1(S)$. $\mu\in M_1(S)$ is $P_t$-invariant if and only if for all $t > 0$: $P_t^*\mu=\mu$. By exam a continuous Feller semigroup $P_t$ admits an invariant probability measure $\mu$ on $S$ if for for all $\e > 0$ there is a compact set $K$ such that $$ \exists x\in S\, \forall t > 0:\quad P_t(x,K^c) < \e~. $$ This in particular holds if $S$ is compact. The following theorem is more or less a consequence of corollary: $\proof$ We'd just like to notice the necessity of the last statement: for $f\in\dom L$ and $f(x_0)=\sup\{f(x):x\in S\}$ the function $h(x)\colon=-f(x)+f(x_0)$ is positive and $h\in\dom L$. Since $h(x_0)=0$ and $P_th(x_0)\geq0$ it follows that $Lh(x_0)\geq 0$ and therefore: $Lf(x_0)\leq-f(x_0)L1=0$. $\eofproof$ Diffusions on compact Riemannian manifolds $S$ are typical examples for Feller semigroups - the third condition in theorem is just the maximum principle for diffusion operators!
A special class of Feller semigroups
For compact $S$ we infer from exam that every continuous Feller semigroup $P_t$ on $C(S)$ admits an invariant probability measure $\mu$. Obviously, $P_t$ is a continuous contraction semigroup on $L_1(\mu)$ and a contraction on $L_\infty(\mu)$. If in addition $\mu$ is unique, then for all $f\in C(S)$ $A_tf$ converges point-wise to $\int f\,d\mu$ - cf. exam. Hence $P_t$ is ergodic in $L_1(\mu)$ and by proposition the Mean Ergodic Theorem holds on any space $L_p(\mu)$, $1\leq p < \infty$, but what about the space $C(S)$, i.e. what about uniform convergence? We will only be concerned with a very particular class of continuous Feller semigroups, which are characterized by the relative compactness of the set $\{P_tf:t\geq0\}$ for all $f\in C(S)$. For this class of continuous Feller semigroups we infer from the Mean Ergodic Theorem that $A_tf$ converges uniformly as $t\to\infty$. However theorem will give a much stronger result.
Suppose the continuous Feller semigroup $P_t$ on a compact space $S$ improves the modulus of continuity of any function $f\in C(S)$, i.e. there is a continuous function $h:\R_0^+\rar\R_0^+$ such that $h(0)=0$ and for all $x\in S$, all $t\geq0$ and all $f\in C(S)$:
$$
\o_{P_tf}(x,r)\colon=\sup\{|P_tf(y)-P_tf(x)|:d(x,y) < r\}
\leq h(\o_{f}(x,r))
$$
Deduce from the Arzelà-Ascoli Theorem that the set $\{P_tf:t\geq0\}$ is relatively compact in $C(S)$.
A probability measure $\mu$ on $S$ is said to be strictly positive, if for all open subsets $U\neq\emptyset$: $\mu(U) > 0$.
The following result turns out to be extremely useful in formulating necessary criteria for compactness:
$\proof$
For $0\leq f\in C(S)$ put
$$
m(f)(t)\colon=\min\{P_tf(x):x\in S\}~.
$$
Then $m(f)$ is continuous (by exam) and $0\leq m(f)(t)\leq\norm f$. It's also increasing: we have $P_tf-m(f)(t)\geq0$ and thus: $P_sP_tf-m(f)(t)\geq0$, i.e. $m(f)(s+t)\geq m(f)(t)$. Hence put
$$
m(f)\colon=\lim_{t\to\infty}m(f)(t)
$$
and choose a sequence $t_n\uar\infty$ such that $P_{t_n}f$ converges in $C(S)$ to some function $g\in C(S)$. For $t\geq0$ we conclude by uniform convergence:
\begin{equation}\tag{MCS2}\label{mcseq2}
\min P_tg(S)
=\lim_{n\to\infty}\min P_{t+t_n}f(S)
=\lim_{n\to\infty}m(f)(t+t_n)=m(f)~.
\end{equation}
We are going to check that this implies for all $f\in C(S)$: $g(x)=m(f)$. Putting $t=0$ in \eqref{mcseq2}, we get: $g=m(f)+h$ for some $h\geq0$. If $h\neq0$, then we have by assumption for some $a > 0$ depending on $h$: $P_ah > 0$, hence $\min P_ah(S) > 0$ but this contradicts
\eqref{mcseq2}. Thus the only possible limit of $P_tf$ is $m(f)$ and the limit $\lim P_tf$ exists for all $f\in C(S)$.The mapping $f\mapsto m(f)$ is linear, positive with norm $1$. Hence by the Riesz representation Theorem there is a probability measure $\mu$ on $S$, such that $m(f)=\int f\,d\mu$. If $m(f)=0$ for some $0\leq f\leq1$, $f\neq0$, then by monotonicity of $m(f)$: $0=m(f)(a)$ for some $a > 0$ depending on $f$, which implies $f=0$. Hence $\mu$ is strictly positive. $\eofproof$
On a two point set the stochastic matrix
$$
P\colon=\left(\begin{array}{cc}
0&1\\
1&0\\
\end{array}\right)
$$
satisfies the assumptions in exam, but $P^{2n}=1$ and $P^{2n+1}=P$.
Let $S$ be a compact metric space, $w_1,\ldots,w_n:S\rar S$ $L$-Lipschitz maps on $S$ and $p_1,\ldots,p_n\in(0,1)$ such that $\sum p_j=1$ (cf. exam). If $L\leq1$ and
$$
Pf(x)\colon=\sum_j p_jf(w_j(x)),
$$
then for all $f\in C(S)$ the set $\{P^nf:n\in\N_0\}$ is relatively compact in $C(S)$. 2. If $L < 1$, then $P^*:M_1(S)\rar M_1(S)$ has a unique fixed point. Hint: Use Banach's fixed point theorem and the metric in exam.
Suppose $X$ is a vector field on a compact Riemannian manifold $S$ such that its flow $\theta_t$ is an isometry for all $t\in\R$ - in that case $X$ is called a Killing field. Then for all $f\in C(S)$ the set $\{f\circ\theta_t:t > 0\}$ is relatively compact by the Arzelà-Ascoli Theorem and thus by the Mean Ergodic Theorem the limit $Qf\colon=\lim_{t\to\infty}A_tf$ exists in $C(S)$ and $Q$ is the projection onto the kernel of $X$ mapping the image of $X$ to $0$.
If $d > 2$ the spectral theorem for skew symmetric operators shows that there are orthogonal unit vectors $u,v\in S^{d-1}$ and $\l\in\R$ such that $Au=\l v$ and $Av=-\l u$. Hence $e^{tA}|\lhull{u,v}$ is rotation by $t\l$ and the non-constant function $f:S^{d-1}\rar\R$,
$$
f(x)\colon=\la x,u\ra^2+\la x,v\ra^2
$$
is obviously invariant under $e^{tA}$:
Page Rank
A certain number $n$ of websites form a directed graph: if on site $j$ there is a link to site $k$ we put $a_{jk}=1$, otherwise wet set $a_{jk}=0$ - in any case we put $a_{jj}=0$. $A\colon=(a_{jk})$ is said to be the adjacency matrix of the sites. We get probably the simplest rating of a site $k$ by just counting the number of sites pointing to this site, i.e. $$ \mu_k\colon=\sum_j a_{jk} $$ If you want to give some more weight to sites, that do not point to a lot of other sites, you may define $$ \mu_k\colon=\sum_j a_{jk}/n_j \quad\mbox{where}\quad n_j\colon=\deg^-(j)=\sum_k a_{jk}~. $$ $n_j$ is the number of different links on site $j$ and $\sum_j a_{jk}$ is the number of so called back-links of site $k$, i.e. the number of sites, that point to site $k$. The problem with this specification: the operator of a site may establish loads of sites pointing only to her site of interest. But we can circumvent such problems by not assigning the weight $1/n_j$ to each site but $\mu_j/n_j$. Thus we obtain the linear system of equations $$ \mu_k=\sum_j \mu_ja_{jk}/n_j~. $$ Putting $p_{jk}\colon=a_{jk}/n_j$ and $P\colon=(p_{jk})$ we get the matrix equation: $\mu=P^t\mu$, where $\mu=(\mu_1,\ldots,\mu_n)^t$, i.e. $\mu$ is an invariant measure for the stochastic matrix $P$.Convolution on Homogeneous Spaces
Cf. e.g. Y. Benoist, J-P. Quint: Introduction to Random Walks on Homogeneous Spaces. Let $G,S$ be Polish and assume in addition that $(G,\cdot)$ is a topological group, i.e. both the multiplication $(g,h)\mapsto gh$ and the inversion $g\mapsto g^{-1}$ are continuous. Moreover assume $G$ acts continuously on $S$, i.e. there is a continuous map $(g,x)\mapsto gx$ from $G\times S$ on $S$ such that for all $x\in S$: $ex=x$ and for all $g,h\in G$: $g(hx)=(gh)x$. In this case $S$ is said to be a homogeneous space or a $G$-space. We will also assume that $G$ acts transitively on $S$, i.e. for all $x\in S$: $Gx=S$. Now let $m$ be a probability measure on $G$, we construct a random walk, i.e. a Markov chain, on $S$ as follows: given $X_0$ we choose $g\in G$ according to $m$ and put $X_1=gX_0$: $$ P(x,A) =\P^x(X_1\in A) =\P^x(gx\in A) =m(\{g:gx\in A\}) =\int_G\d_{gx}(A)\,m(dg) =\int_G I_A(gx)\,m(dg) $$ and therefore we get for the Markov operator: \begin{equation}\tag{MCS3}\label{mcseq3} Pf(x) =\int_S\int_G f(y)\d_{gx}(dy)\,m(dg) =\int_G f(gx)\,m(dg) \end{equation} and its adjoint $P^*:M_1(S)\rar M_1(S)$: \begin{equation}\tag{MCS4}\label{mcseq4} \int_S f\,dP^*\mu=\int_S\int_G f(gx)\,m(dg)\,\mu(dx) \end{equation} $P$ is actually Feller, i.e. $P:C_b(S)\rar C_b(S)$. In case $S=G$ this is just the definition of the convolution of the measures $m$ and $\mu$. Generalizing this we simply define the convolution $m*\mu$ of the measures $m\in M_1(G)$ and $\mu\in M_1(S)$ by \eqref{mcseq4}, i.e. $m*\mu\colon=P^*\mu$. We have by Fubini $$ m*\mu(A) =\int_S\int_G I_A(gx)\,m(dg)\,\mu(dx) =\int_G\mu(g^{-1}A)\,m(dg) $$ Let $F:G\times S\rar S$ denote the map $(g,x)\mapsto gx$, then for any $A\sbe S$: $F^{-1}(A)_g=\{x:gx\in A\}=g^{-1}A$ and thus $$ (m\otimes\mu)_F(A) =m\otimes\mu(F^{-1}(A)) =\int_G\mu(F^{-1}(A)_g)\,m(dg) =\int_G\mu(g^{-1}A)\,m(dg) =m*\mu(A), $$ i.e. $m*\mu$ is the image measure of the product measure $m\otimes\mu$ under the action of $G$ on $S$. On any locally compact group $G$ there is a left-invariant Radon measure $m$, i.e. $m(K) < \infty$ for all compact sets $K$ and for all $g\in G$ and all Borel sets $A\sbe G$: $m(gA)=m(A)$, cf. e.g. wikipedia; equivalently $$ \forall g\in G\,\forall f\in C_c(S): \int f(gh)\,m(dh) =\int f(h)\,m(dh) < \infty~. $$ If $G$ is compact, then there is a unique normalized Haar measure $m$ on $G$, i.e. $m(G)=1$ and $m(gA)=m(Ag)=m(A)$. If $S$ is compact, then by exam there is at least one $m$-invariant probability measure $\mu\in M_1(S)$, i.e. $m*\mu=\mu$. We are going to identify this measure $\mu$ for a particular measure $m$: the Haar measure on the group $G$. Assume $\mu\in M_1(S)$ is $m$-invariant, i.e. $m*\mu=\mu$, then for all $g\in G$ and all Borel sets $A\sbe S$: $$ \mu(gA) =\int_G\mu(h^{-1}gA)\,m(dh) =\int_G\mu((g^{-1}h)^{-1}A)\,m(dh) =\int_G\mu(h^{-1}A)\,m(dh) =\mu(A) $$ in other words: $\mu$ is a $G$-invariant Borel probability measure on $S$. If this probability measure $\mu$ is unique it's called the normalized $G$-measure on $S$.On the other hand for any $G$-invariant probability measure $\mu\in M_1(S)$ and all $m\in M_1(G)$ we have: $$ m*\mu(A) =\int_G\mu(h^{-1}A)\,m(dh) =\mu(A)m(G)=\mu(A)~. $$ Thus if $\mu\in M_1(S)$ is a $G$-invariant probability measure, then $\mu$ is $m$-invariant (i.e. $m*\mu=\mu$) for all $m\in M_1(G)$. If $m$ is the normalized Haar measure on a compact group $G$, then $\mu\in M_1(S)$ is $m$-invariant if and only if $\mu$ is $G$-invariant.
Suppose $m$ be a symmetric probability measure on the compact group $G$, i.e. for all Borel subsets $A$ of $G$: $m(A)=m(A^{-1})$. 1. If $\mu$ is a $G$-invariant probability measure on $S$, then the associated Markov operator $P:L_2(\mu)\rar L_2(\mu)$,
$$
\forall x\in S:\quad
Pf(x)\colon=\int_G f(gx)\,m(dg)
$$
is self-adjoint and its conductance is given by
$$
K=\inf\Big\{\frac1{\mu(A)\mu(A^c)}\int_G\mu(gA\sm A)\,m(dg):0 < \mu(A) < 1\Big\}~.
$$
2. If $\mu$ is the only $m$-invariant probability measure on $S$, then $P$ is ergodic on e.g. $L_1(\mu)$.
3. If $m$ is the normalized Haar measure and $\mu$ is the only $G$-invariant probability measure on $S$, then the sequence of random variables $X_n$ is i.i.d with distribution $\mu$.
$\proof$
1. To establish self-adjointness we take $f_1,f_2\in C(X)\sbe L_2(\mu)$ and infer from Fubini's theorem and the symmetry of $m$:
\begin{eqnarray*}
\int_S Pf_1(x)f_2(x)\,\mu(dx)
&=&\int_S\int_G f_1(gx)f_2(x)\,m(dg)\,\mu(dx)\\
&=&\int_G\int_S f_1(gx)f_2(x)\,\mu(dx)\,m(dg)\\
&=&\int_G\int_S f_1(x)f_2(g^{-1}x)\,\mu(dx)\,m(dg)\\
&=&\int_S\int_G f_1(x)f_2(g^{-1}x)\,m(dg)\,\mu(dx)\\
&=&\int_S\int_G f_1(x)f_2(gx)\,m(dg)\,\mu(dx)
=\int_S f_1(x)Pf_2(x)\,\mu(dx)~.
\end{eqnarray*}
For any Borel subset $A$ of $S$ we have:
$$
K(A)
\colon=\int_A\int_G I_{A^c}(gx)\,m(dg)\,\mu(dx)
=\int_G\mu(A\cap g^{-1}A^c)\,m(dg)
=\int_G\mu(A\sm g^{-1}A)\,m(dg)
=\int_G\mu(gA\sm A)\,m(dg)~.
$$
2. This follows from exam.3. If $m$ is the normalized Haar measure and $\mu$ is the only $G$-invariant probability measure on $S$, then the sequence of random variables $X_n$ is i.i.d with distribution $\mu$.
3. Putting for any $x\in S$: $F:G\rar S$, $F(g)=gx$ and $\nu(A)\colon=m(F\in A)=m(\{g: gx\in A\})$ we find that for all $h\in G$: $F(hg)=hF(g)$ and thus $$ \nu(hA) =m(\{g: F(g)\in hA\}) =m(\{g:F(h^{-1}g)\in A\}) =m(h^{-1}\{g:F(g)\in A\}) =m(\{g:F(g)\in A\}) =\nu(A) $$ By uniqueness of the $G$-invariant probability measure we conclude: $\nu=\mu$. $\eofproof$ Conditions of existence and uniqueness for $G$-invariant probability measures: If a group $G$ acts isometrically on a compact metric space $(S,d)$, i.e. $$ \forall x,y\in S\,\forall g\in G:\quad d(gx,gy)=d(x,y), $$ then there exists a $G$-invariant Borel probability measure $\mu$ on $S$, i.e. $\mu(gA)=\mu(A)$; in this case it follows that $\mu$ is $m$-invariant for all $m\in M_1(G)$! Uniqueness of $G$-invariant probability measures is always guaranteed because we presuppose that $G$ acts transitively on $S$. As $G$ acts isometrically, the set $\{P^nf:n\in\N_0\}$ is relatively compact in $C(S)$ by the Arzelà-Ascoli Theorem. If we assume in addition that for all $0\leq f\in C(S)$, $f\neq0$, there is some $n$ such that for all $x\in S$: $P^nf(x) > 0$, then by theorem $P^nf$ converges to $\int f\,d\mu$ in $C(S)$ and $\mu$ is strictly positive and its also the only $m$-invariant probability measure on $S$.
For $S=S^{d-1}$ and $G=\OO(d)$ with normalized Haar measure $m$ the normalized surface measure $\s$ on $S^{d-1}$ is the unique normalized $G$-measure and this is the only probability measure on $S^{d-1}$, which is $m$-invariant, i.e. $m*\s=\s$. Cf. section for sampling points on $\OO(d)$ distributed according to $m$.
This can be generalized easily:
Under the assumptions of the previous exam show that
$$
d(x,y)\colon=\inf\{n:yx^{-1}\in B^n\}
\quad\mbox{where}\quad
B^0\colon=\{e\},
B^n\colon=\{x_1\cdots x_n:x_1,\ldots,x_n\in B\}
$$
is a metric on $G$ and the conductance of the Markov chain $X_n$ is bounded from below by
$$
\frac{|G|}{|B|}\inf\Big\{\frac1{|A|}\sum_{g\in B}|gA\sm A|:0 < |A|\leq\frac{|G|}2\Big\}
\geq\frac{|G|}{|B|}\inf\Big\{\frac{|[d_A=1]|}{|[d_A=0]|}:0 < |A|\leq\frac{|G|}2\Big\}~.
$$
As the set $[d_A=1]$ can be regarded as the 'boundary' of $A$ the quotient $|[d_A=1]|/|[d_A=0]|$ is called the isoperimetric quotient of the set $A$. 2. Put $R\colon=B\sm\{e\}$ and define a simple graph on $G$ by joining the pair $(x,y)$ if and only if $yx^{-1}\in R$. This graph is called the Cayley graph of $(G,R)$, cf. e.g. Cayley graphs.
Gibbs Algorithm and Ising Model
Gibbs Algorithm
Cf. e.g. Gibbs sampling: Let $S$ be a discrete Polish space, $N\in\N$ and $U$ a random variable with values in the product space $S^N$. Denote by $\mu$ the distribution of $U$, i.e. $\mu(\o)=\P(U=\o)$. For $\o,\eta\in S^N$ we will write $\o\sim_j\eta$ if for all $k\neq j$: $\o_k=\eta_k$, i.e. $\o$ and $\eta$ differ at most in slot $j$. Now put $$ q(\o,\eta)\colon=\left\{\begin{array}{cl} \frac{\mu(\eta)}{N\sum_{\z\sim_j\o}\mu(\z)}&\mbox{if $\exists j:\ \eta\sim_j\o$}\\ 0&\mbox{otherwise} \end{array}\right. $$ Then $\mu$ is reversible for the Markov chain with stochastic matrix $(q(\o,\eta))$: If $\o$ and $\eta$ differ only in slot $j$, then $\z\sim_j\o$ if and only if $\z\sim_j\eta$ and therefore $$ \mu(\o)q(\o,\eta) =\frac{\mu(\o)\mu(\eta)}{N\sum_{\z\sim_j\o}\mu(\z)} =\frac{\mu(\o)\mu(\eta)}{N\sum_{\z\sim_j\eta}\mu(\z)} =\mu(\eta)q(\eta,\o)~. $$ If $\o$ and $\eta$ differ in more than one slot, then both $q(\o,\eta)$ and $q(\eta,\o)$ vanish. By exam the Markov chain is reversible with respect to $\mu$. So we are left with the construction of the Markov chain $X_n$: Suppose $X_n=\o$; choose one of the slots with probability $1/N$; suppose we've chosen slot $j$ then choose $X_{n+1}=\eta$ with probability $$ \frac{\mu(\eta)}{\sum_{\z\sim_j\o}\mu(\z)} $$Ising's model
Ising's model of a ferromagnetic metal. Let $A\sbe\Z^3$ be a finite subset and put $\O=\{-1,+1\}^A=\{-1,+1\}^N$: we interpret $A$ as the positions of atoms of a cubic structure and for $\o\in\O$ and $x\in A$ $\o(x)=\pm1$ as the spin of the atom in position $x$. $\O$ is called the space of states. Every state has a certain energy \begin{equation}\label{markoveq6} H(\o)\colon=\a\sum_{z\in A}\o(z)-\tfrac12\b\sum_{(y,z)\in R}\o(y)\o(z), \end{equation} where $\a,\b$ are real constants and e.g. $(x,y)\in R$ if and only if $\sum_j|x_j-y_j|\leq1$, i.e. $R(x)$ contains at most seven points: $$ x,(x_1\pm1,x_2,x_3),(x_1,x_2\pm1,x_3),(x_1,x_2,x_3\pm1)~. $$ Suppose $\b > 0$, then the coupling term is minimized for parallel spins - that's the ferromagnetic situation. On the other hand the case $\b < 0$ describes the antiferromagnetic situation.If the system is in thermodynamic equilibrium at temperature $T$ the entropy theorem asserts that the probability of state $\o$ is given by $$ \mu(\o)\colon=\frac1Z\exp(-H(\o)/T) $$ Since there are loads of states the normalizing constant $Z$ cannot be calculated by brute force - even a small number of e.g. $N=100$ atoms amounts to $2^{100}$ states. In order to determine $Z$ we will approximate the mean value of a function $F:\O\rar\R$ by means of the Gibbs algorithm: in this case we have $\o\sim_x\eta$ if for all $y\neq x$: $\o(y)=\eta(y)$ and $\eta(x)=-\o(x)$ or $\eta=\o$; in the first case we have $$ q(\o,\eta) =\frac{e^{-H(\eta)/T}}{N(e^{-H(\eta)/T}+e^{-H(\o)/T})} \quad\mbox{and in the second}\quad q(\o,\o)=\frac{e^{-H(\o)/T}}{N(e^{-H(\eta)/T}+e^{-H(\o)/T})}~. $$ Now $H(\o)$ and $H(\eta)$ have almost all summands in common: $$ H(\o)=H_0+\o(x)\Big(\a-\b\sum_{z\in R(x)}\o(z)\Big),\quad H(\eta)=H_0-\o(x)\Big(\a-\b\sum_{z\in R(x)}\o(z)\Big)~. $$ Thus putting $p(x)\colon=\exp(-\o(x)(\a-\b\sum_{z\in R(x)}\o(z))/T)$, we get $$ q(\o,\eta) =\frac{1/p(x)}{N(p(x)+1/p(x))} \quad\mbox{and}\quad q(\o,\o)=\frac{p(x)}{N(p(x)+1/p(x))}~. $$ Hence we choose the sequence of states $\o_0,\o_1,\ldots$ as follows
- At time $n=0$ put $\o_0(x)=\pm1$ arbitrary.
- Suppose $X_n=\o_n$ then we choose with probability $1/N$ one of the positions, $x$ say, compute $$ p(x)\colon=\exp(-\o_n(x)(\a-\b\sum_{z\in R(x)}\o_n(y))/T) $$ and change the spin of the atom in position $x$ with probability $1/(p(x)^2+1)$.
- Since $\mu$ is reversible the Markov chain is ergodic by e.g. exam and by subsection we get: $$ \lim_{n\to\infty}\frac1{n+1}\sum_{j=0}^n F(\o_j)= \sum_{\o\in\O} F(\o)\mu(\o) $$ for $\P^\mu$-almost all $(\o_0,\o_1,\ldots)\in\O^{\N_0}$.
Sampling random variables
Uniform distributions on $S^{d-1}$
We start off with two independent random variables $U$ and $V$ uniformly distributed on $(0,1)$ and put $$ (Z_1,Z_2)\colon=-\sqrt{2\log U}(\cos(2\pi U),\sin(2\pi V))~. $$ Then $Z_1,Z_2$ are independent standard normals. Now if $Z_1,\ldots,Z_d$ are independent standard normals, then $$ X\colon=\frac{(Z_1,\ldots,Z_d)}{\sqrt{\sum Z_j^2}} $$ is uniformly distributed on the unit sphere $S^{d-1}$. Of course instead of the normals $(Z_1,\ldots,Z_d)$ we may take any random variable in $\R^d$ with rotational invariant distribution.Uniform distributions on $B_2^d$ and $B_1^d$
How can we generate random variables uniformly distributed on $B=B_2^d$ or $B=B_1^d$? In small dimensions, e.g. $d=2$ we choose two independent random variables $U$ and $V$ uniformly distributed on $(-1,1)$ and take $X=(U,V)$ if $U^2+V^2 < 1$. In higher dimensions (e.g. $d > 10$) this produces an enormous amount of useless trials: the unit ball $B_2^d$ of $\ell_2^d$ has very small volume in comparison to $[-1,1]^d$. Assume $Z_1,\ldots,Z_d$ are independent standard normals and let $R:(0,1)\rar(0,1)$, $R(t)=t^{1/d}$ be an independent random variable on $(0,1)$, then $\P(R\leq r)=r^d$ and it is easily seen that $$ X\colon=R\frac{(Z_1,\ldots,Z_d)}{\sqrt{\sum Z_j^2}} $$ is uniformly distributed on $B_2^d$.2. To generate uniform distribution on $B_1^d$ put $$ Z_1\colon=-\log(U)\sign(U-1/2) $$ then the distribution of $Z_1$ is the Laplace distribution, i.e. the distribution on $\R$ with density $\tfrac12e^{-|x|}$. Now again take independent copies and another independent random variable $R:(0,1)\rar(0,1)$, $R(t)=t^{1/d}$. Then $$ X\colon=R\frac{(Z_1,\ldots,Z_d)}{\sum|Z_j|} $$ is uniformly distributed on $B_1^d$.
Uniform distributions on $\OO(d)$
Again we start with $d$ independent standard gaussian random variables $X_1,\ldots,X_d$ in $\R^d$ - these are just $d^2$ independent standard gaussians in $\R$. Then we apply the Gram-Schmidt orthonormalization procedure to the $d$ vectors $X_1,\ldots,X_d$ and get $d$ orthonormal vectors $U_1,\ldots,U_d$. Finally merge these vectors to form an orthogonal matrix $U$.Real valued random variables
A distribution function $F:\R\rar[0,1]$ is an increasing, right continuous function such that $\lim_{t\to-\infty}F(x)=0$ and $\lim_{t\to\infty}F(t)=1$. There is a straight forward way to generate a random variable $T:[0,1)\rar\R$ on the probability space $([0,1),\l)$ with distribution function $F$, i.e. $$ \l(T\leq x)=F(x)~. $$ We just have to put $$ T(x)\colon=\inf\{t:\,F(t) > x\}~. $$ To prove that $T$ has distribution $F$ we need to verify that $\l(T\leq t)=F(t)$. So suppose $T(x)\leq t$ then there is some sequence $t_n\dar T(x)$ such that $F(t_n) > x$; by right continuity of $F$ it follows that $F(T(x))\geq x$ and by monotonicity: $x\leq F(t)$. On the other hand $x < F(t)$ implies: $T(x)\leq t$. Hence $$ [0,F(t))\sbe[T\leq t]\sbe[0,F(t)] \quad\mbox{and therefore}\quad \l(T\leq t)=F(t)~. $$ If $F$ is strictly increasing and continuous then $T=F^{-1}$.
Suppose $f:[0,1]\rar[0,1]$ is measurable and $X_1,X_2,\ldots$ an i.i.d. sequence in $[0,1]$ with distribution $\mu$. Define
$$
N\colon=\inf\{2n:\,X_{2n-1}\leq f(X_{2n})\}
$$
then
$$
\P(X_N>t)
=\int_t^\infty\mu((0,f(x)])\,\mu(dx)/
\int_0^\infty\mu((0,f(x)])\,\mu(dx)~.
$$
If $\mu=\l$, then $X_N$ has density $f/\int f\,d\l$. Suggested solution.
In general it's not a good idea to sample random variables by means of limit theorems. Anyhow, here is an example of symmetric $p$-stable random variables, whose distribution is in general not given by a 'nice' formula:
Let $0 < p\leq2$. A random variable $X$ is called a symmetric $p$-stable r.v. with parameter $\s$, if its characteristic function $\vp_X(t)\colon=\E\exp(itX)$ is given by
$$
\exp\Big(-\tfrac12\s^p|t|^p\Big)~.
$$
For $p\in(0,2)$ let $X$ be a symmetric r.v. with distribution $\P(|X| > x)=\min\{1,x^{-p}\}$. If $X_1,\ldots,X_n$ denote independent copies of $X$ then the r.v.
$$
S_n\colon=\frac1{n^p}\sum_{j=1}^nX_j
$$
converge in distribution to a symmetric $p$-stable r.v. with parameter (suggested solution):
$$
\s_p^p=2\int_0^\infty\frac{1-\cos(u)}{u^{1+p}}\,dx~.
$$
Hastings-Metropolis Filter
Suppose $\mu$ is a not necessarily finite Borel measure on the Polnish space $S$ and $X_n$ a Markov chain reversible with respect to $\mu$ with Markovian transition function $P(x,A)$. Let $F:S\rar[0,\infty]$ be a measurable function, such that $Z\colon=\int F\,d\mu < \infty$. Then $$ \pi(dx)\colon=\frac1ZF(x)\mu(dx) $$ is a probability measure. We will define a new Markov chain $Y_n$ which is reversible with respect to $\pi$:- If $Y_n=x$ choose $X_{n+1}$ according to the distribution $P(x,.)$.
- If $F(X_{n+1}) > F(x)$ then put: $Y_{n+1}=X_{n+1}$.
- If $F(X_{n+1}) \leq F(x)$ choose an independent random variable $\b$ such that $\P(\b=1)=F(X_{n+1})/F(x)$ and put $Y_{n+1}=X_{n+1}$ if $\b=1$ and $Y_{n+1}=x$ if $\b=0$.
<Home> Last modified: Mon Nov 4 14:27:06 CET 2024