The Complex Numbers
Definitions and conventions
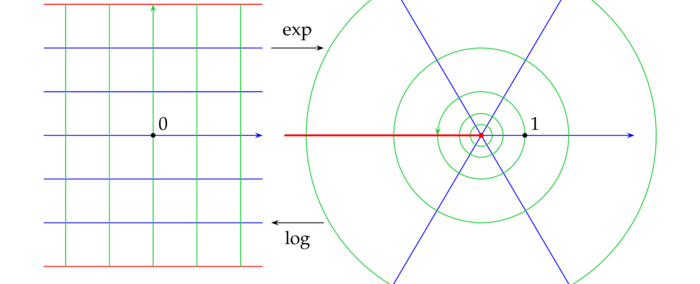
Identifizieren wir die Zahlen aus $\R$ mit Punkten auf einer Zahlengerade, so ist es natürlich, Punkte aus $\R^2$ (d.h. geordnete Paare $(x,y)$) mit Punkten einer Ebene zu identifizieren. Wir betrachten diese Objekte als Zahlen - die sogenannten komplexen Zahlen - indem wir diese Menge mit einer Addition und einer Multiplikation versehen: \begin{eqnarray*} (x_1,y_1)+(x_2,y_2)&\colon=&(x_1+x_2,y_1+y_2) \quad\mbox{und}\\ (x_1,y_1)(x_2,y_2)&\colon=&(x_1x_2-y_1y_2,x_1y_2+x_2y_1)~. \end{eqnarray*} Verwenden wir den Buchstaben $i$ für die komplexe Zahl $(0,1)$ und identifizieren wir die reelle Zahl $x$ mit der komplexen Zahl $(x,0)$, so sehen wir erstens: $i^2=-1$ (i.e. $(0,1)^2=(-1,0)$) und zweitens existiert zu jedem $z\in\C$ genau ein $x\in\R$ und genau ein $y\in\R$, so daß: $z=x+iy$ (i.e. $(x,y)=(x,0)+(0,1)(y,0)$). $x$ heißt der Realteil von $z$ (geschrieben $\Re z$) und $y$ der Imaginärteil von $z$ (geschrieben $\Im z$). Wir führen weiters folgende Bezeichnung ein: ist $z=x+iy\in\C$ eine komplexe Zahl, so heißt die komplexe Zahl $\bar z\colon=x-iy$ die zu $z$ konjugiert komplexe Zahl und die nicht negative Zahl $$ |z|=(x^2+y^2)^{1/2}=(z\bar z)^{1/2} $$ der Betrag von $z$. Es gelten dann die Beziehungen: \begin{equation}\label{comeq1}\tag{TCN1} \cl{z+w}=\bar z+\bar w,\ \cl{zw}=\bar z\bar w, \ |z+w|\leq|z|+|w|,\ |zw|=|z||w|~. \end{equation} Falls $z$ von $0$ verschieden ist, dann gilt: $z^{-1}\colon=\bar z/|z|^2$. Man bestätigt leicht, daß $(\C,+,.)$ ein Körper und $\R$ ein Unterkörper von $\C$ ist.
Sei $P(z)=z^n+\sum_{j < n} a_jz^j$ ein Polynom und $C\colon=\sup\{|a_j|:j < n\}$. Dann liegen sämtliche Nullstellen von $P$ in $\{z\in\C:|z|\leq C+1\}$. Lösungsvorschlag.
Bestimmen Sie zu $n\in\N$ die Menge aller $z\in\C$ für die gilt:
$|z^n/n!|=\sup\{|z^k/k!|:k\in\N\}$.
Binomsche Formel: Seien $z,w\in\C$ und $n\in\N_0$, dann
gilt:
\begin{equation}\label{comeq2}\tag{TCN2}
(z+w)^n=\sum_{k=0}^n{n\choose k}z^kw^{n-k}
\quad\mbox{wobei}\quad
{n\choose k}\colon=\frac{n!}{k!(n-k)!}
\quad\mbox{und}\quad
0!\colon=1~.
\end{equation}
Den Vektorraum $\C^n$ versehen wir i.A. stets mit dem kanonischen euklidischen Produkt
$$
\forall x,y\in\C^n:\quad
\la x,y\ra\colon=\sum_{j=1}^nx_j\bar y_j
$$
und der zugehörigen Norm $\Vert x\Vert\colon=\sqrt{\la x,x\ra}$: $(\C^n,\Vert.\Vert)$ ist dann ein $n$-dimensionaler euklidischer Raum (oder ein $n$-dimensionaler Hilbertraum). Die offene Einheitskugel von $(\R^n,\Vert.\Vert)$ bzw. $(\C^n,\Vert.\Vert)$ bezeichnen wir mit $B_2^n$ bzw. $B_2^{2n}$.
Domains
Sei $(X,d)$ ein metrischer Raum. Mit $B_r(x)$ oder $B(x,r)$ bezeichnen wir die offene Kugel um $x$ mit dem Radius $r$, also: $B_r(x)=\{y\in X:d(x,y) < r\}$. Ist insbesondere $X=\C$, so bezeichnen wir mit $D_r$ die offene Kreisscheibe $B_r(0)$ und mit $D$ den offenen Einheitskreis $D_1$. Die Menge $\TT\colon=S^1\colon=\pa D$ nennt man auch den eindimensionalen Torus oder den Einheitskreis. Für jede Teilmenge $A$ von $X$ nennt man die Mengen $$ A^\circ\colon=\bigcup\{U: U\sbe A, U\mbox{ offen}\} \quad\mbox{bzw.}\quad \cl{A}\colon=\bigcap\{C: C\spe A, C\mbox{ abgeschlossen}\} $$ das Innere bzw. den Abschluß von $A$. $\pa A\colon=\cl{A}\sm A^\circ$ heißt der Rand von $A$. Ein metrischer Raum $(X,d)$ heißt separabel, wenn es eine höchstens abzählbare Teilmenge $D$ von $X$ gibt, die dicht liegt in $X$, d.h. $\cl D=X$. Z.B. sind $\R^n$, $\C^n$ und $L_p(\R^n)$ für $p < \infty$ separabel; $L_\infty([0,1])$ ist hingegen nicht separabel. Ein metrischer Raum $(X,d)$ heißt zusammenhängend, wenn aus $X=U\cup V$, $U,V$ offen und $U\cap V=\emptyset$ folgt: $U=\emptyset$ oder $V=\emptyset$ - eine zusammenhängende Menge läßt sich also nicht in zwei nicht leere, disjunkte und offene Teilmengen zerlegen (oder die einzigen Teilmengen von $X$ die sowohl offen als auch abgeschlossen sind, sind $\emptyset$ und $X$). Allgemeiner ist eine offene Teilmenge $\O$ eines normierten Raumes genau dann zusammenhängend, wenn es zu allen Punkten $z_0,z_1\in\O$ eine stetige (oder glatte oder polygonale) Kurve $c:[0,1]\rar\O$ gibt mit: $c(0)=z_0$ und $c(1)=z_1$: Die Menge alle Punkte $z_1$, zu denen es ein solche Kurve $c$ gibt ist nicht leer, offen und abgeschlossen; falls $\O$ also zusammenhängend ist, dann stimmt diese Menge mit $\O$ überein. Sei umgekehrt $U,V$ eine offene Zerlegung von $\O$, $z_0\in U$, $z_1\in V$ und $c:[0,1]\rar\O$ die stetige Kurve mit $c(0)=z_0$ und $c(1)=z_1$, dann ist $c^{-1}(U),c^{-1}(V)$ eine offene Zerlegung von $[0,1]$ mit $0\in c^{-1}(U)$ und $1\in c^{-1}(V)$. Nach Proposition ist dies aber unmöglich.
Eine offene und zusammenhängende Teilmenge $\O$ eines metrischen Raumes $X$ nennen wir ein Gebiet.
$\proof$
$X$ is genau dann nicht zusammenhängend, wenn zwei disjunkte, nicht leere und offene Teilmengen $U$ und $V$ von $X$ existieren, so daß $X=U\cup V$. Setze $f\colon=I_U$, also $f|U=1$ und $f|V=0$, so ist $f$ stetig und nicht konstant. Falls umgekehrt $f:X\rar\{0,1\}$ stetig und nicht konstant ist, dann sind $U\colon=[f=1]\colon=\{x\in X: f(x)=1\}$ und $V\colon=[f=0]$ zwei disjunkte, nicht leere und offene Teilmengen von $X$ mit $U\cup V=X$.
$\eofproof$
Sind $A,B$ zusammenhängende Teilmengen des metrischen Raumes $X$, so daß
$A\cap B\neq\emptyset$, dann ist auch $A\cup B$ zusammenhängend, denn jede stetige Funktion $f:A\cup B\rar\{0,1\}$ ist sowohl auf $A$ als auch $B$ konstant und da $A\cap B\neq\emptyset$, müssen diese Konstanten gleich sein. Dies erlaubt die Definition der Zusammenhangskomponente $Z_A(x)$ eines Punktes $x$ einer Teilmenge $A$ von $X$: $Z_A(x)$ ist die Vereinigung aller zusammenhängenden Teilmengen $Z$ von $A$, die den Punkt $x$ enthalten. Zwei Zusammenhangskomponenten $Z_1$ bzw. $Z_2$ von $A$ sind dann entweder disjunkt oder gleich! Ferner sind, wie das folgende Beispiel zeigt, Zusammenhangskomponenten stets abgeschlossen in $A$.
1. Sei $z\in Z$, dann ist $z\in A^c$ und da $A^c$ offen ist: $B_r(z)\sbe A^c$. Weiters ist $Z\cap B_r(z)\neq\emptyset$, also muß $B_r(z)\cup Z$ zusammenhängend sein und weil $Z$ eine Zusammenhangskomponente von $A^c$ ist: $B_r(z)\cup Z\sbe Z$, i.e. $B_r(z)\sbe Z$.2. Angenommen $z\in\pa Z\cap A^c$, dann gibt es ein $r > 0$, so daß $A^c$ die offene Kugel $B_r(z)$ um $z$ enthält; da $z\in\pa Z$, enthält $B_r(z)$ einen Punkt aus $Z$ und damit muß $Z$ die offene Kugel $B_r(z)$ umfassen; $z$ kann somit kein Randpunkt von $Z$ sein.
Convex, star shaped and triangularizable sets
Sei $X$ ein normierter Raum; eine Teilmenge $\O$ von $X$ heißt konvex, wenn für alle $z_0,z_1\in\O$ gilt: die Strecke $[z_0,z_1]\colon=\{(1-t)z_0+tz_1:t\in[0,1]\}$ liegt in $\O$. $\O$ heißt sternförmig, wenn ein Punkt $z_0\in\O$ existiert, so daß für alle $z_1\in\O$ und alle $t\in[0,1]$ gilt: $(1-t)z_0+tz_1\in\O$.Eine Teilmenge $A$ von $\C$ heißt triangulierbar, wenn endlich viele (abgeschlossene) Dreiecke $\D_1,\ldots,\D_n$ mit paarweise disjunktem Inneren existieren, so daß $\bigcup\D_j=A$ und für alle $j\neq k$ die Menge $\D_j\cap\D_k$ entweder eine gemeinsame Seite, ein gemeinsamer Eckpunkt oder leer ist. Der Rand jeden Dreiecks $\D_j$ besteht aus drei Seiten und für jede dieser Seiten $s$ gibt es genau zwei Möglichkeiten: entweder gibt es genau ein anderes Dreieck $\D_k$, das gleichfalls die Seite $s$ besitzt oder es gibt kein weiteres solches Dreieck. Die Menge der Seiten, die Seite von genau einem Dreieck sind bildet dann den Rand $\pa A$ von $A=\bigcup\D_j$.
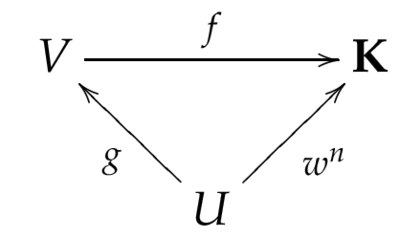
Ist $K$ eine kompakte Teilmenge einer offenen Menge $\O\sbe\C$, so gibt es eine triangulierbare Teilmenge $T$ mit $K\sbe T^\circ\sbe T\sbe\O$. Falls darüber hinaus $\O$ konvex ist, so kann man auch $T$ konvex wählen.
$\R$-linear and $\C$-linear maps
Die folgenden Abschnitte sollen u.A. die Parallelität zwischen dem reellen und dem komplexen Differentialkalkül demonstrieren, d.h. die Resultate bleiben unabhängig vom zugrundeliegenden Körper gültig, ob dieser nun $\R$ oder $\C$ ist. Im Weiteren sei daher $\bK$ entweder der Körper $\R$ der reellen Zahlen oder der Körper $\C$ der komplexen Zahlen. $X,Y,\ldots$ bezeichnen stets Banachräume über $\bK$ und $L(X;Y)$ den Raum der stetigen linearen Abbildungen $A:X\rar Y$ mit der Operatornorm $$ \norm A\colon=\sup\{\norm{Ax}:\Vert x\Vert\leq1\}~. $$ Zwar kann man jeden komplexen Vektorraum $X$ auch als einen Vektorraum über $\R$ betrachten, aber die Algebra $L(X)\colon=L(X;X)$ bleibt von dieser Interpretation nicht unverändert: z.B. ist $\C$ selbst als Vektorraum über $\R$ zu $\R^2$ isomorph, aber $L(\C)$ ist isomorph zu $\C$; hingegen ist $L(\R^2)$ zu $\Ma(2,\R)$ - den reellen $2\times2$-Matrizen - isomorph. Dies liegt einfach daran, daß eine $\R$-lineare Abbildung nicht $\C$-linear sein muß: Wir betrachten dazu eine beliebige $\R$-lineare Abbildung $A$ von $\R^2$ in $\C$, also $$ A:(x,y)\mapsto(a_{11}x+a_{12}y)+i(a_{21}x+a_{22}y) $$ Als Abbildung von $\C$ in $\C$ ist dies die Abbildung: $$ A^\C:x+iy\mapsto(a_{11}x+a_{12}y)+i(a_{21}x+a_{22}y) $$ Nach Definition ist $A^\C$ genau dann $\C$-linear wenn für alle $\l\in\C$ und alle $z,w\in\C$ gilt: $A^\C(\l z)=\l A^\C(z)$ und $A^\C(z+w)=A^\C(z)+A^\C(w)$. Die zweite Beziehung folgt aus der $\R$-Linearität von $A$; hingegen garantiert die $\R$-Linearität von $A$ die erste Bedingung nur für alle $\l\in\R$. Die entscheidende Beziehung ist daher: $A^\C(iz)=i A^\C(z)$ und diese gilt genau dann, wenn $a_{11}=a_{22}$ und $a_{12}=-a_{21}$. Ist dies der Fall, so ist $A^\C$ die Multiplikation mit der komplexen Zahl $w\colon=a_{11}+ia_{21}$.Plane geometry
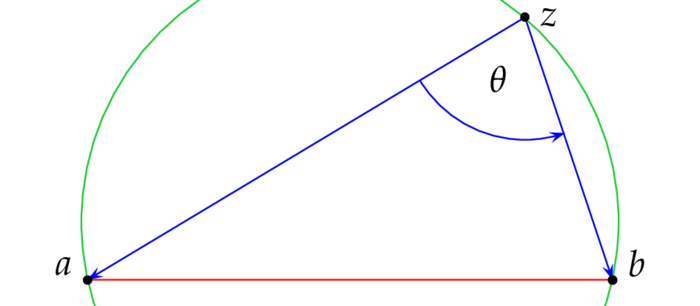
Die Abbildung $(x,y)\mapsto x+iy$ ist eine $\R$-lineare Isometrie von $\R^2$ auf $\C$; somit ist es naheliegend die elementaren geometrischen Begriffe in der Ebene mithilfe komplexer Zahlen zu formulieren: Seien $(x_j,y_j)$ Punkte in $\R^2$ und $z_j\colon=x_j+iy_j$ die entsprechenden komplexen Zahlen; das innere Produkt von $(x_1,y_1)$ und $(x_2,y_2)$ läßt sich dann einfach schreiben als $\Re(z_1\bar z_2)$; $-\Im(z_1\bar z_2)$ besitzt gleichfalls eine geometrische Bedeutung: es ist der orientierte Flächeninhalt des von den Vektoren $(x_1,y_1)$ und $(x_2,y_2)$ (in dieser Reihenfolge) aufgespannten Parallelogramms.Seien $(a,b)\in\R^2$ ein normierter Vektor und $R_E$ die Spiegelung an $E\colon=\{(x,y)\in\R^2:ax+by=0\}$. Wir möchten nun diese Spiegelung in komplexer Form schreiben: Die Spiegelung an $E$ ist in $\R^2$ gegeben durch $R_E(x,y)=(x,y)-2\la(x,y),(a,b)\ra(a,b)$. Seien $w=a+ib$ und $z=x+iy$, dann gilt also in komplexer Form: $$ R_E(z) =z-2\Re(z\bar w)w =z-(z\bar w+\bar zw)w =z-z|w|^2-\bar zw^2 =-w^2\bar z~. $$ Das folgende Beispiel zeigt, daß Drehungen in $\R^2$ Multiplikationen in $\C$ mit normierten komplexen Zahlen entsprechen: Jede $\C$-lineare Abbildung $W:\C\rar\C$ ist die Multiplikation mit einer komplexen Zahl $w$, i.e. (falls $W$ nicht die Nullabbildung ist): $W(z)=wz=aw_0z$ mit $a\colon=|w| > 0$ und $w_0\colon=w/|w|$. Die Abbildung $z\mapsto az$ nennt man eine Homothetie oder eine Streckung und die Abbildung $z\mapsto w_0z$ ist, wie wir gesehen haben eine Drehung. Reell betrachtet sind also $\C$-lineare Abbildung $W:\C\rar\C$ Drehstreckungen, d.h. Kompositionen von Drehungen und Streckungen.
Sei $\l$ das Lebesguemaß auf $\C=\R^2$; für $w\in\C$ und $A\sbe\C$ seien $w+A=\{w+a:a\in A\}$ bzw. $wA\colon=\{wa:a\in A\}$. Dann folgt aufgrund der Translationsinvarianz des Lebesguemaßes: $\l(w+A)=\l(A)$; ferner erhalten wir für jedes Dreieck $\D$: $\l(wD)=|w|^2\l(\D)$, denn wir können o.B.d.A. annehmen, daß $\D=\D(0,z_1,z_2)$ und damit $$ 2\l(w\D)=|\Im(wz_1\bar w\bar z_2)|=|w|^2|\Im(z_1\bar z_2)|=2|w|^2\l(\D)~. $$ Somit gilt aber auch für jedes Rechteck $Q$: $\l(wQ)=|w|^2\l(Q)$, d.h. die Maße $\l_w(A)\colon=\l(wA)$ und $|w|^2\l$ stimmen auf den Rechtecken überein. Nach dem Satz von Caratheodory aus der Maßtheorie gilt daher für alle Lebesgue-meßbaren Teilmenge $A$ von $\C$: $\l(wA)=|w|^2\l(A)$.
Seien $z_1,z_2,z_3\in\C$. Unter der Strecke zwischen $z_1$ und $z_2$ bzw. dem Dreieck mit den Eckpunkten $z_1,z_2,z_3$ versteht man die Mengen
\begin{eqnarray*}
[z_1,z_2]&\colon=&
\{t_1z_1+t_2z_2:\,t_1,t_2\geq0,\,t_1+t_2=1\}\quad\mbox{bzw.}\\
\D(z_1,z_2,z_3)&\colon=&
\{t_1z_1+t_2z_2+t_3z_3:\,t_1,t_2,t_3\geq0,\,t_1+t_2+t_3=1\}~.
\end{eqnarray*}
Die Strecken $[z_1,z_2],[z_2,z_3]$ und $[z_3,z_1]$ nennt man die Seiten des Dreiecks - es gilt: $\pa\D(z_1,z_2,z_3)=[z_1,z_2]\cup[z_2,z_3]\cup[z_3,z_1]$. Zeigen Sie:
$$
h\colon=\inf\{|(1-t)z_1+tz_2|:t\in\R\}
=\frac{|\Im(z_1\bar z_2)|}{|z_2-z_1|}~.
$$
$h$ heißt die Höhe des Dreiecks $\D(0,z_1,z_2)$ auf die Seite $[z_1,z_2]$. Lösungsvorschlag.
Seien $z_1,z_2,1$ die Ecken eines Dreiecks $\D$ in $\C$ mit $|z_1|,|z_2| < 1$. Zeigen Sie, daß es eine positive Konstante $C$ gibt, so daß für alle $z\in\D$: $|1-z|\leq C(1-|z|)$. Lösungsvorschlag
Bestimmen Sie das Bild des Kreises $K\colon=\{z\in\C:|z-1|=1\}$ unter der Abbildung $z\mapsto z^2$. Lösungsvorschlag
Sei $z=x+iy$ mit $y > 0$, dann ist $|G(z)|$ das Verhältnis der Abstände zwischen $i$ und $z$ bzw. $-i$ und $z$; diese ist offensichtlich kleiner als $1$. $i-z=w(i+z)$: $i-iw=z(w+1)$, also: $z=i(1-w)/(1+w)$.
Eine Fülle an Aufgaben kann man u.A. in dem Buch von T. Andreescu & D. Andrica finden.
AC circuits
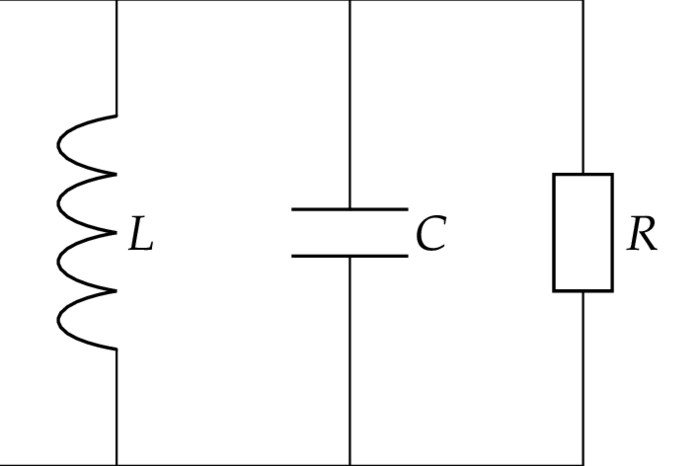
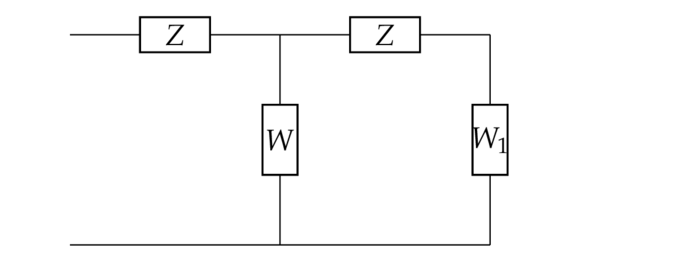
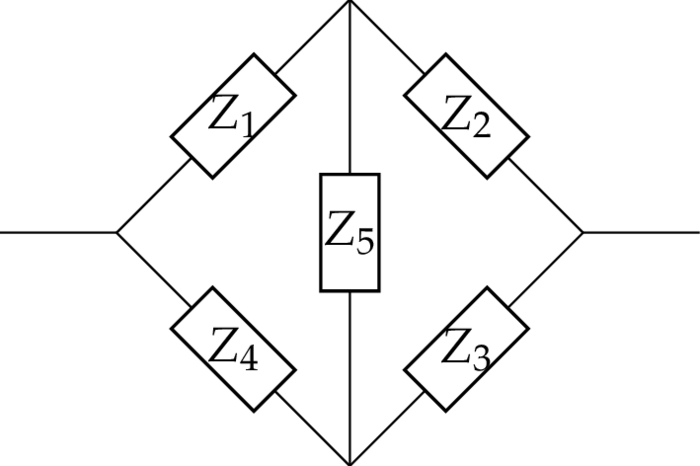
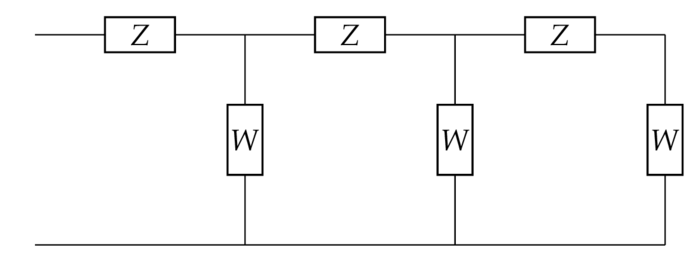
Cf. e.g. Feynman Lectures II, 22 oder wikipedia. Ein elektrischer Schaltkreis besteht aus Elementen (Kondensator, Spule, Widerstand etc.), die mit idealen Leitern zu einem Netzwerk verbunden sind. Legt man eine Wechselspannung $V_0e^{i\o t}$ der Frequenz $\o/2\pi$ an, so durchfließt jedes der Elemente $j$ zu Zeitpunkt $t$ ein (komplexer) Strom $I_je^{i\o t}$ und der (komplexe) Spannungsabfall längs des Elements ist $V_je^{i\o t}$ - nimmt man von beiden den Real- oder Imaginärteil, so erhält man den tatsächlichen Strom bzw. den tatsächlichen Spannungsabfall. Das Verhältnis $Z_j\colon=V_j/I_j$ nennt man in der Wechselstromtechnik die Impedanz des Elements $j$. Z.B. ist die Impedanz eines Kondensators bzw. einer Spule bzw. eines Widerstands: $$ \frac1{i\o C},\quad i\o L,\quad R $$ wobei die nicht negativen reellen Konstanten $C$ bzw. $L$ bzw. $R$ die Kapazität bzw. die Induktanz bzw. der Widerstand genannt werden. Ein komplexers Netzwerk setzt sich u.A. aus Elementen zusammen, die z.B. seriell oder parallel geschalten sind. Das Problem besteht nun darin die Impedanz des Netzwerks zu bestimmen, was zum Teil mit folgender Proposition gelingt: Z.B. erhalten wir für die Impedanz $Z$ des folgenden Netzwerks:
