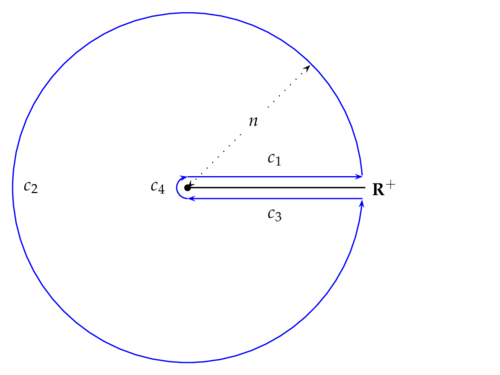
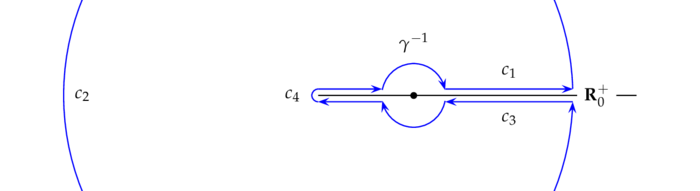
The Cauchy-Goursat Theorem
The Cauchy-Goursat theorem
Der folgende Satz ist zentral für die gesamte Funktionentheorie; es handelt sich um eine einfachere Form der sogenannten Cauchyschen Integralformel (vgl. Satz) - einfacher deshalb, weil wir nur Kreise als Integrationswege zulassen!
$\proof$
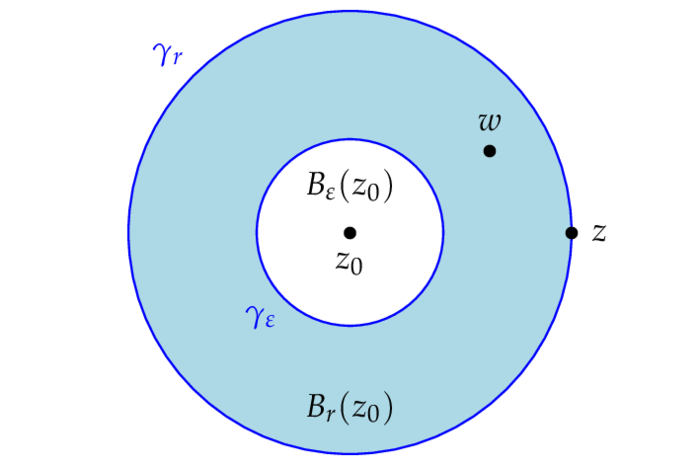
1. Wir zeigen zunächst, daß für alle $w\in\O$ und alle $0 < r < d(w,\O^c)$:
\begin{equation}\label{cgteq1}\tag{CGT2}
f(w)=\frac{1}{2\pi i}\int_{\g_w}\frac{f(z)}{z-w}\,dz
\end{equation}
Sei $w\notin E$, dann ist die durch
\begin{equation}\label{cgteq2}\tag{CGT1}
g_w(z)\colon=\left\{\begin{array}{cl}
\frac{f(z)-f(w)}{z-w}&\mbox{falls $z\neq w$}\\
f^\prime(w)&\mbox{falls $z=w$}
\end{array}\right.
\end{equation}
definierte Funktion stetig auf $\O$ und in $\O\sm(E\cup\{w\})$ differenzierbar. Nun ist $\g_w$ innerhalb $\O$ zur konstanten Kurve $t\mapsto w$ konturhomotop und somit folgt nach dem Cauchyschen Integralsatz:
$$
0=\int_{\g_w}g_w(z)\,dz
=\int_{\g_w}\frac{f(z)}{z-w}\,dz-\int_{\g_w}\frac{f(w)}{z-w}\,dz
$$
Da $\int_{\g_w}(z-w)^{-1}\,dz=2\pi i$, folgt die Beziehung \eqref{cgteq1} für alle $w\in\O\sm E$. Nun ist aber sowohl $f$ als auch $w\mapsto\int_{\g_w}f(z)(z-w)^{-1}\,dz$ stetig - wenn wir z.B, den Radius $r$ von $\g_w$ gleich $(1-\e)d(w,\O^c)$ setzen, also folgt die Gültigkeit der Beziehung \eqref{cgteq1} für alle $w\in\O$ aufgrund der Dichtheit von $\O\sm E$ in $\O$.
2. Wir zeigen nun, daß für alle $\z\in B_r(w)$ - also nicht nur für $\z=w$:
\begin{equation}\label{cgteq3}\tag{CGT3}
f(\z)=\frac{1}{2\pi i}\int_{\g_w}\frac{f(z)}{z-\z}\,dz~.
\end{equation}
Mit $r_1\colon=r-|\z-w|$ ist die Kurve $\g_w$ innerhalb $B_r(w)\sm\{\z\}$ zur Kurve $\g_\z(t)=\z+r_1e^{it}$ konturhomotop; nach dem Cauchyschen Integralsatz sind daher die Integrale von $f(z)/(z-\z)$ über $\g_\z$ und $\g_w$ gleich.
3. Die Formel für die $n$-te Ableitung folgt nach Differentiation unter dem Integral \eqref{cgteq3}; insbesondere erhalten wir:
$$
\norm{f^{(n)}(w)}
\leq\frac{n!}{2\pi r^n}\int_{-\pi}^\pi\norm{f(w+re^{it})}\,dt
\leq\frac{n!}{r^n}\sup\{\norm{f(z)}:|z-w|=r\}
$$
und damit ist der Konvergenzradius der Taylor-Reihe von $f$ im Punkt $w$ mindestens $r$.
$\eofproof$
Achtung: Der Satz von Cauchy-Goursat könnte folgende Vermutung nahelegen: Angenommen wir haben eine glatte Funktion $f:\pa D\rar\C$, die auf dem Rand $\pa D$ des Einheitskreises definiert ist; definiere
$$
\forall z\in D:\qquad
F(z)\colon=\frac1{2\pi i}\int_{\pa D}\frac{f(w)}{w-z}\,dw~.
$$
Vermutung: $F$ ist auf $D$ analytisch und stimmt auf $\pa D$ mit $f$ übereinstimmt. Zwar ist $F$ analytisch und $\lim_{r\dar1}F(re^{i\theta})$ existiert auch, aber dieser Limes stimmt i.A. nicht mit $f(e^{i\theta})$ überein! Cf. Abschnitt.
$\proof$
Für $k\in\N$, $k > n$ und $r > 0$ gilt nach Satz für alle $|w| < r/2$:
$$
f^{(k)}(w)=\frac{k!}{2\pi}
\int_0^{2\pi}\frac{f(re^{it})}{(re^{it}-w)^{k+1}}re^{it}\,dt
$$
Mit $r\to\infty$ folgt dann nach Voraussetzung:
$$
\tnorm{f^{(k)}(w)}
\leq k!\limsup_{r\to\infty}(C_0+C_1r^n)(r-r/2)^{-k-1}r
=0~.
$$
$\eofproof$
Aus diesem Korollar folgt z.B.:
- Jedes nicht konstante Polynom $p$ besitzt eine Nullstelle in $\C$. Andernfalls wäre $f(z)\colon=1/p(z)$ komplex differenzierbar und beschränkt, also konstant.
- Für jede ganze, nicht konstante Funktion $f:\C\rar\C$ ist $f(\C)$ dicht in $\C$. Andernfalls gäbe es ein $z_0\in\C$, so daß $g(z)\colon=1/(f(z)-z_0)$ eine ganze beschränkte Funktion wäre, also konstant sein müßte.
- Angenommen $f,g:\C\rar\C$ sind ganze Funktionen, so daß für alle $z$: $|f(z)|\leq|g(z)|$. Dann gibt es eine Konstante $|c|\leq1$, so daß $f=cg$: Da die Nullstellen $E$ von $g$ isoliert sind - falls $g$ nicht konstant ist, was wir annehmen können, und $h\colon=f/g$ stetig ist (cf. Beispiel), dann muß $h$ nach dem Satz von Cauchy-Goursat eine ganze Funktion sein und somit muß $h$ nach Korollar konstant sein. Alternative: cf. Proposition.
- Zu jedem beschränkten linearen Operator $A:X\rar X$ eines Banachraumes $X$ existiert ein $z\in\C$, so daß $A-z:X\rar X$ kein Isomorphismus ist, cf. Proposition.
Harmonic functions
Ist $f:\O(\sbe\C)\rar X$ komplex differenzierbar und $\cl B_r(w)\sbe\O$, so gilt nach dem Satz von Cauchy-Goursat:
$$
f(w)
=\frac1{2\pi}\int_{-\pi}^\pi f(w+re^{it})\,dt
$$
i.e. der Funktionswert von $f$ im Punkt $w$ ist gleich dem Mittelwert der Funktionswerte von $f$ auf dem Kreis mit dem Mittelpunkt $w$ und Radius $r$ - stetige Funktionen mit dieser Eigenschaft nennt man harmonisch. Allgemeiner nennt man eine stetige Funktion $f:\O\rar\R$ auf einem Gebiet $\O\sbe\R^n$ harmonisch, wenn für alle $x\in\O$ und alle $r > 0$ mit $\cl{B_r(x)}\sbe\O$ gilt:
$$
f(x)=\int_{S^{n-1}}f(x+r\z)\,\s(d\z)
$$
wobei $\s$ das normalisierte (i.e. $\s(S^{n-1})=1$) rotationsinvariante Borelmaß auf der Sphäre $S^{d-1}$ ist.
$\proof$
Nach der Kettenregel sowie der Definition von $\nabla f$ gilt $\pa_rf(x+r\z)=df(x+r\z)(\z)=\la\nabla f(x+r\z),\z\ra$, also
$$
\pa_r\int_{S^{n-1}}f(x+r\z)\,\s(d\z)
=\int_{S^{n-1}}\la\nabla f(x+r\z),\z\ra\,\s(d\z)~.
$$
Bezeichnen wir mit $X(y)$ das Vektorfeld $\nabla f(x+ry)$, mit $M$ die Einheitskugel $B_1(0)$ und mit $N=\z$ das äußere Normalvektorfeld von $S^{n-1}=\pa M$, so folgt nach dem Divergenzsatz:
$$
\int_{\pa M}\la X,N\ra=-\int_M\divergence X
$$
und da $\divergence X(y)\colon=-\sum\pa_jX_j(y)=r\D f(x+ry)$ bedeutet dies:
$$
\int_{S^{n-1}}\la\nabla f(x+r\z),\z\ra\,\s(d\z)
=-\frac{r}{\vol{}(S^{n-1})}\int_{B_1(0)}\D f(x+ry)\,dy~.
$$
Ist also $f$ harmonisch, so folgt für alle $0 < r < 1$: $\int_{B_1(0)}\D f(x+ry)\,dy=0$, was aufgrund der Stetigkeit von $\D f$ nur dann möglich ist, wenn $\D f(x)=0$. Umgekehrt folgt aus $\D f=0$, daß $r\mapsto\int_{S^{n-1}}f(x+r\z)\,\s(d\z)$ konstant ist; da dieses Integral für $r\dar 0$ gegen $f(x)$ konvergiert, muß $f$ harmonisch sein.
$\eofproof$
Sei nun $h:D_R(\sbe\C)\rar\R$ irgendeine integrierbare Funktion mit der Eigenschaft, daß für alle $0 < r < R$: $t\mapsto h(re^{it})$ konstant ist, dann gilt für jede harmonische Funktion $f:D_R\rar\R$:
\begin{equation}\label{cgteq4}\tag{CGT4}
\int_{D_R}f(z)h(z)\,\l(dz)
=\int_0^R\int_{-\pi}^\pi f(re^{it})h(re^{it})r\,dt\,dr
=2\pi f(0)\int_0^R rh(r)\,dr
=f(0)\int_{D_R(w)}h(z)\,\l(dz)
\end{equation}
Wir betrachten nun speziell den Fall der Fourier-Transformierten von $fh$, wobei $f:\R^2(=\C)\rar\C$ harmonisch sein soll und $h(z)=e^{-|z|^2/4t}$ für $t > 0$. Als Integrierbarkeitsbedingung setzen wir voraus, daß für ein $c > 0$:
$$
\lim_{z\to\infty}f(z)e^{-c|z|}=0~.
$$
Mittels quadratischer Ergänzung erhalten wir: $-|z|^2/4t-i\Re(z\bar w)=-|z+2itw|^2/4t-t|w|^2$, also
$$
\frac1{2\pi}\int_{\C}f(z)e^{-|z|^2/4t-i\Re(z\bar w)}\,\l(dz)
=\frac1{2\pi}\int_{\C}f(z)e^{-|z+2itw|^2/4t-t|w|^2}\,\l(dz)
=\frac{e^{-t|w|^2}}{2\pi}\int_{\C}f(z-2itw)e^{-|z|^2/4t}\l(dz)~.
$$
Nach \eqref{cgteq4} folgt wegen $\int_{\C}e^{-|z|^2/4t}\,\l(dz)=4\pi t$:
$$
\frac1{2\pi}\int_{\C}f(z)e^{-|z|^2/4t-i\Re(z\bar w)}\,\l(dz)
=2e^{-t|w|^2}f(-2itw)~.
$$
Mit $z=x+iy$ und $w=u+iv$ folgt: $\Re(z\bar w)=xu+yv$ und somit ist $(u,v)\mapsto2e^{-t|w|^2}f(-2itw)$ die Fourier-Transformierte der Funktion $(x,y)\mapsto f(x+iy)e^{-(x^2+y^2)/4t}$. Cf. Unterabschnitt.
Harmonic polynomials in $\R^n$
Für harmonische Polynome $H:\R^2\rar\C$ gilt nach der oben erwähnten Anwendung der Beziehung \eqref{cgteq4}:
$$
\frac1{2\pi}\int_{\R^2}H(x)e^{-\Vert x\Vert^2/4t-i\la x,y\ra}\,dx
=2te^{-t\Vert y\Vert^2}H(-2ity)~.
$$
Diese Beziehung bleibt in jeder Dimension gültig (cf. Unterabschnitt):
Sei $H$ ein $l$-homogenes harmonisches Polynom, $-l < \a < n+l$, $\vp\in C_c^\infty(\R^n)$ und $\wh\vp$ die Fourier-Transformierte von $\vp$, dann gilt mit einer von $l,\a$ und $n$ abhängigen Konstante $\g(l,\a,n)$:
$$
\int_{\R^n}\frac{H(x)}{\Vert x\Vert^{l+n-\a}}\,\wh\vp(x)\,dx
=\g(l,\a,n)\int_{\R^n}\frac{H(x)}{\Vert x\Vert^{l+\a}}\,\vp(x)\,dx
$$
$\proof$
Für alle $t > 0$ gilt:
$$
\int H(x)e^{-\Vert x\Vert^2/4t}e^{-i\la x,y\ra}\,dx
=H(-2ity)(4\pi t)^{n/2}e^{-t\norm y^2}~.
$$
Multiplikation mit $(2\pi)^{-n/2}\vp(y)$ und Integration über $y$ ergibt aufgrund der $l$-Homogenität von $H$:
$$
\int H(x)e^{-\Vert x\Vert^2/4t}\wh\vp(x)\,dx
=(-2i)^l2^{n/2}t^{l+n/2}\int H(y)e^{-t\norm y^2}\vp(y)\,dy~.
$$
Multiplizieren wir beide Seiten mit $f(t)$ und integrieren über $t$ von $0$ bis $\infty$, so folgt:
$$
\int H(x)\wh\vp(x)
\Big(\int_0^\infty f(t)e^{-\Vert x\Vert^2/4t}\,dt\Big)\,dx\\
=(-2i)^l2^{n/2}\int H(y)\vp(y)\Big(
\int_0^\infty f(t)t^{l+n/2}e^{-t\norm y^2}\,dt
\Big)\,dy~.
$$
Setzen wir $F(r)=\int_0^\infty f(t)e^{-r^2/4t}\,dt$ und $G(r)= \int_0^\infty f(t)t^{l+n/2}e^{-tr^2}\,dt$, so folgt:
$$
\int H(x)\wh\vp(x)F(\Vert x\Vert)\,dx
=(-2i)^l2^{n/2}\int H(y)G(\norm y)\vp(y)\,dy,
$$
Sei insbesondere $f(t)=t^{-\b}$, dann ist
$$
F(r)=r^{-2\b+2}4^{\b-1}\G(\b-1)
\quad\mbox{und}\quad
G(r)=r^{2\b-2l-n-2}\G(-\b+l+n/2+1)
$$
Die Behauptung folgt dann für $2\b=l+n-\a+2$.
$\eofproof$
Bemerkung:
Ist $P$ ein $l$-homogenes harmonisches Polynom, so heißt die Einschränkung $Y:S^{n-1}\rar\C$, $Y=P|S^{n-1}$, eine Kugelfunktion des Grades $l$. Sei $H_l^n$ der von den Kugelfunktionen des Grades $l$, $l\in\N_0$, erzeugte Unterraum von $L_2(S^{n-1})$, dann bilden diese eine orthogonale Zerlegung von $L_2(S^{n-1})$, i.e.
$$
L_2(S^{n-1})=\bigoplus_{l=0}^\infty H_l^n
\quad\mbox{und für alle $l\neq k$:}\quad
H_l^n\perp H_k^n~.
$$
Die Bedeutung der Kugelfunktionen in der Quantenmechanik bzw. der theoretischen Chemie liegt an folgender Eigenschaft: sie sind sozusagen der richtungsabhängige Teil der Eigenfunktionen des Schrödinger-Operators $\D+V$ mit einem beliebigen rotationssymmetrischen Potential $V$. Im Fall $n=3$ nennt man diese Eigenfunktionen auch Orbitale und insbesondere für $l=0$ bzw. $1$ bzw. $2$ heißen sie $s-$ bzw. $p-$ bzw. $d$-Orbitale; ferner gilt: $\dim H_l^3=2l+1$. Den Index $l$ nennt man auch die Drehimpulsquantenzahl und eine Basis von $H_l^3$ indiziert man mit $m\in\{-l,-l+1,\ldots,0,1,\ldots,l\}$ und nennt $m$ die Magnetquantenzahl. Mit ein paar Vereinfachungen liefert dies eine ziemlich genaue Beschreibung des Aufbaus der Periodentafel sowie der Bindungseigenschaften der Elemente, cf. e.g. Feynman Lectures III, 19-6 The periodic table.
Maximum principle
Wir betrachten im Folgenden differenzierbare Funktionen $f:\O\rar X$, die auf einer offenen Teilmenge $\O$ von $\C^n$ definiert sind und Werte in einem komplexen Banachraum $X$ annehmen.
$\R^n$ bzw. $\C^n$ mit den üblichen euklidischen Normen sind z.B. strikt konvex.
Für einen Banachraum $X$ sind folgende Aussagen äquivalent (Lösungsvorschlag):
- $X$ ist strikt konvex, i.e. für alle $x,y\in S_X$ mit $y\neq x$ gilt: $\norm{x+y} < 2$.
- Für alle $x\in S_X$, alle $y\in\cl{B_X}$ mit $y\neq x$ gilt: $\norm{x+y} < 2$.
- Für alle $x\neq y\in S_X$ und alle $t\in(0,1)$ gilt: $\norm{(1-t)x+ty} < 1$ - die Einheitssphäre $S_X$ enthält keine nicht trivialen Strecken.
- Sind $x,y\in X\sm\{0\}$, so daß $\norm{x+y}=\Vert x\Vert+\norm y$, dann gibt es ein $\l > 0$, so daß $y=\l x$.
Ferner ist $L_p(\mu)$ genau dann strikt konvex, wenn $1 < p < \infty$: in der Minkowski-Ungleichung $\norm{X+Y}_p\leq\norm X_p+\norm Y_p$ gilt für $p\in(1,\infty)$ genau dann Gleichheit, wenn für ein $\l\geq0$: $X=\l Y$ oder $Y=\l X$. Falls also $\norm X_p=\norm Y_p=1$ und $\norm{X+Y}_p=2$, dann folgt $\l=1$, i.e. $Y=X$. $L_1(\mu)$ und $L_\infty(\mu)$ sind nicht strikt konvex, denn für je zwei Indikatorfunktionen $I_A$ und $I_B$ gilt: $\norm{I_A+I_B}_1=\mu(A)+\mu(B)-\mu(A\cap B)$; falls $A\cap B=\emptyset$, dann folgt: $\norm{I_A+I_B}_1=\norm{I_A}_1+\norm{I_B}_1$. Falls $\mu(A\cap B) > 0$, dann folgt: $\norm{I_A+I_B}_\infty=\norm{I_A}_\infty+\norm{I_B}_\infty$.
Wir benötigen im Beweis des Maximumprinzips folgende Eigenschaft strikt konvexer Räume:
$\proof$
1. Für alle $\z\in\C^n$ mit $\norm\z=1$ ist $g_\z(z)\colon=f(w+z\z)$ auf einer offenen Umgebung von $\cl D_r$ differenzierbar, also
$$
f(w)
=g_\z(0)
=\frac1{2\pi}\int_0^{2\pi}g_\z(re^{it})\,dt
=\frac1{2\pi}\int_0^{2\pi}f(w+r\z e^{it})\,dt
$$
und damit:
\begin{equation}\label{cgteq5}\tag{CGT5}
\norm{f(w)}
\leq\frac1{2\pi}\int_0^{2\pi}\norm{f(w+r\z e^{it})}\,dt
\leq\sup\{\norm{f(z)}:\Vert z-w\Vert=r\}~.
\end{equation}
2. Angenommen die Funktion $\vp$ nimmt in einem Punkt $w\in\O$ ihr Maximum an, dann gibt es ein $r >0$, so daß für alle $z\in B_r(w)$: $\vp(z)\leq\vp(w)$ und in der Beziehung \eqref{cgteq5} muß für alle $\z\in\C^n$ mit $\norm\z=1$ Gleichheit gelten, d.h. erstens muß $\vp$ auf $B_r(w)$ konstant sein und zweitens muß gelten:
\begin{equation}\label{cgteq6}\tag{CGT6}
\forall\norm\z=1:\qquad
\int_0^{2\pi}\norm{f(w+r\z e^{it})}\,dt
=\Big\Vert\int_0^{2\pi}f(w+r\z e^{it})\,dt\Big\Vert
\end{equation}
Sei $A\colon=\{z\in\O:\vp(z)=\vp(w)\}$, dann ist $A$ aufgrund der Stetigkeit von $\vp$ abgeschlossen in $\O$; $A$ ist aber auch offen in $\O$, denn $\vp$ nimmt in jedem Punkt $z\in A$ ihr Maximum an; nach dem oben angeführten Argument gibt es daher zu jedem $z\in A$ ein $r > 0$, so daß $\vp$ auf $B_r(w)$ konstant ist. Da $\O$ zusammenhängend ist, folgt: $A=\O$ und somit muß $\vp$ konstant sein.
Ist nun weiters $X$ strikt konvex, so folgt aus der Beziehung \eqref{cgteq6} und Beispiel: $f(w+r\z e^{it})=F_\z(t)f(w)$ mit $F_\z(t)\geq0$ und $F_\z(t)\norm{f(w)}=\norm{f(w)}$, also $F_\z(t)=1$, i.e. $f$ ist auf $B_r(w)$ konstant gleich $f(w)$ und da $\O$ zusammenhängend ist, folgt wiederum daß $f$ auf $\O$ konstant ist.
3. Sei $M\colon=\sup\{\vp(z):z\in K\}$, dann ist $M$ abgeschlossen in $K$ und damit kompakt in $\O$. Angenommen $[\vp=M]\sbe K^\circ$; sei $Z$ eine Zusammenhangskomponente von $[\vp=M]$ in $K$, dann ist $Z$ eine kompakte Teilmenge der offenen Menge $K^\circ$; also existiert ein $\d >0$, so daß $Z_\d\colon=\{z:d(z,Z) < \d\}\sbe K^\circ$. $Z_\d$ ist aber erstens eine echte zusammenhängende Obermenge von $Z$ - aus $Z=Z_\d$ folgte: $Z$ ist eine offene und abgeschlossene Teilmenge von $\O$, also $Z=\emptyset$ oder $Z=\O$ - und zweitens muß nach 2. $\vp$ auf $Z_\d$ konstant sein, was unmöglich ist.
$\eofproof$
Bemerkung: Bleibt die Aussage 2. des obigen Satzes richtig, wenn man Maximum durch lokales Maximum ersetzt? Im strikt konvexen Fall folgt jedenfalls aus der lokalen Konstanz aufgrund des Identitätssatzes die globale Konstant von $f$ und damit auch die von $\vp$.
Das Maximumprinzip ist keine Eigenschaft, die nur für komplex differenzierbare Funktionen gilt, cf. e.g. I. Weinberger; ist z.B. $f:\O(\sbe\R^n)\rar\R$ harmonisch und $\cl{B_r(w)}\sbe\O$. Dann gilt aufgrund der Mittelwerteigenschaft:
$$
\inf\{f(z):\Vert z-w\Vert=r\}\leq f(w)\leq\sup\{f(z):\Vert z-w\Vert=r\}
$$
und daraus folgt, daß eine nicht konstante harmonische Funktion $f$ in keinem Punkt eines Gebiets $\O$ ein lokales Maximum oder ein lokales Minimum annehmen kann - und damit folgt wiederum, daß für jede kompakte Teilmenge $K$ von $\O$ gilt:
$$
\sup_{z\in K}f(z)
=\sup_{z\in\pa K}f(z)
\quad\mbox{und}\quad
\inf_{z\in K}f(z)
=\inf_{z\in\pa K}f(z)~.
$$
Der Begriff 'Maximumprinzip' besitzt in der Mathematik eine wesentlich breitere Bedeutung, z.B. I. Ecklands Variationsprinzip oder verschiedene Nuancen des sogenannte Omori-Yau Maximumprinzips, die in der Geometrie Anwendung finden. Auf z.B. $\R^n$ besagt dieses Prinzip folgendes:
Wir kommen nun aber zu den bekanntesten Implikationen des Maximumprinzips:
Schwarz` lemma
$\proof$
Sei $0 < r < 1$. Da $f(0)=0$ und $f$ auf $D$ analytisch ist, folgt $f(z)=zg(z)$ mit einer analytischen Funktion $g:D\rar X$. Für alle $z\in\pa D_r$ gilt also: $\norm{g(z)}\leq1/r$ und nach dem Maximumprinzip gilt dies für alle $z\in D_r$, i.e. $\norm{f(z)}\leq|z|/r$. Da $r < 1$ beliebig war, folgt: $\norm{f(z)}\leq|z|$.
Falls $\norm{f^\prime(0)}=1$ oder falls ein $z_0\in D\sm\{0\}$ existiert, so daß $|f(z_0)|=|z_0|$, dann nimmt $g$ in einem inneren Punkt ($0$ bzw. $z_0$) von $D$ ihr Maximum an; da $X$ strikt konvex ist, ist $g$ nach dem Maximumprinzip konstant, d.h. $g(z)=u$ mit $\Vert u\Vert=1$ und $f(z)=zu$.
$\eofproof$
Phragmén-Lindelöf theorems
Angenommen $\O$ ist beschränkt, $f:\cl{\O}\rar X$ stetig und auf $\O$ komplex differenzierbar. Falls $\vp\colon=\Vert f\Vert$ nicht konstant ist, dann nimmt $\vp$ nur in Randpunkten von $\O$ ihr Maximum an. Aber
Achtung: Der Betrag einer komplex differenzierbaren Funktion nimmt nicht auf jedem Gebiet $\O$ sein Supremum am Rand an: Sei z.B. $\O\colon=\{z\in\C:\Re z > 0,-\pi/2 < \Im z < \pi/2\}$, dann ist die Funktion $\exp(\exp z)$ zwar auf $\pa\O$ nicht aber auf $\O$ beschränkt, denn für $z=x\pm i\pi/2$ ist
$$
\exp(z)=e^x\exp(\pm i\pi/2)=\pm ie^x
\quad\mbox{und damit:}\quad
|\exp(\exp(z))|=1·
$$
wohingegen für $z=x > 0$: $\exp(\exp(z))=\exp(e^x)$.
Unter gewissen Einschränkungen an das Wachstum der Funktion $f$ für $z\to\infty$ kann man jedoch auf die Beschränktheit schließen. Aussagen dieser Art sind unter dem Namen Phragmén-Lindelöf Sätze zu finden.
$\proof$
Wir wählen $c < b < 1$ und $\e >0$ und setzen
$$
f_\e(z)\colon=f(z)\exp(-\e e^{bz})~.
$$
Dann folgt mit $z=x+iy$:
\begin{eqnarray*}
\norm{f_\e(z)}
&\leq&M|\exp(-\e e^{bz}+e^{cx})|\\
&=&M\exp(-\e e^{bx}\cos(by)+e^{cx})
\leq M\exp(-\e e^{bx}\cos(b\pi/2)+e^{cx})~.
\end{eqnarray*}
Da $c < b < 1$, schließen wir: $\lim_{x\to\infty}f_\e(x+iy)=0$. Also ist $\norm{f_\e}$ für hinreichend große $N$ auf dem Rand von $\O\cap[\Re z\leq N]$ beschränkt durch $1$ - auf $[\Re z > N]$ ist sie ohnehin beschränkt durch z.B. $1/2$. Nach dem Maximumprinzip muß daher für alle $z\in\O$ gelten: $\norm{f_\e(z)}\leq1$. Da $\e > 0$ beliebig war, folgt: $\norm{f}\leq1$.
$\eofproof$
$\proof$
Sei zunächst $X=\C$. Wir können o.B.d.A. annehmen, daß $M_1=1$. Wähle $z_0\in\O$ beliebig aber fix und setze für $n\in\N$:
$$
f_n(z)\colon=\frac{f(z)^nd(z_0,\O^c)}{z-z_0}~.
$$
Dann ist für alle $z\in\pa\O$: $|f_n(z)|\leq1$ und für alle $z\in\O^c$ mit $d(z,z_0)=r$: $|f_n(z)|\leq M_2^nd(z_0,\O^c)/r$. Nach dem Maximumprinzip folgt für alle $z\in\O^{c\circ}\cap D_r$:
$$
|f_n(z)|\leq\max\{1,M_2^nd(z_0,\O^c)/r\},
$$
also mit $r\to\infty$: $|f_n(z)|\leq1$ und damit für alle $n\in\N$:
$$
|f(z)|\leq\Big(\frac{|z-z_0|}{d(z_0,\O^c)}\Big)^{1/n}~.
$$
Mit $n\to\infty$ erhalten wir daher: $|f(z)|\leq1$.
2. Für einen beliebigen komplexen Banachraum $X$ gilt nach 1. für alle $x^*\in X^*$ mit $\norm{x^*}\leq1$: $|x^*(f(z))|\leq1$, i.e. $\norm{f(z)}\leq1$.
$\eofproof$
$\proof$
Definiere $f=P/Q$, dann ist $f$ in einer Umgebung von $D^c$ komplex differenzierbar
und nach Korollar folgt: $|f(z)|\leq1$, also $|P(z)|\leq|Q(z)|$ für alle $z\in D^c$. Sei $|a| >1$ und $R_a\colon=P-aQ$; wir behaupten, daß alle Nullstellen des Polynoms $R_a$ in $D$ liegen, denn aus $R_a(z_0)=0$ folgt entweder $|P(z_0)| >|Q(z_0)|$ oder $Q(z_0)=0$. Nach Proposition liegen daher auch alle Nullstellen von $R_a^\prime=P^\prime-aQ^\prime$ in $D$ und folglich besitzt die Gleichung $P^\prime-aQ^\prime=0$ für kein $|a| > 1$ auf $D^c$ eine Lösung; da $|a| > 1$ beliebig war, folgt für alle $z\notin D$: $|P^\prime(z)|\leq|Q^\prime(z)|$.
$\eofproof$
Sei $P$ ein Polynom des Grades $n$ und $M\colon=\sup\{|P(z)|:|z|=1\}$. Setzen wir $Q(z)\colon=Mz^n$, so gilt für alle $z\in\pa D$: $|P(z)|\leq|Q(z)|$, also nach Korollar für alle $|z|=1$: $|P^\prime(z)|\leq nM$, i.e. es gilt die Bernstein Ungleichung
$$
\sup\{|P^\prime(z)|:|z|=1\}\leq n\sup\{|P(z)|:|z|=1\}
$$
$\proof$
Indem wir $f(z)$ durch $f(z)M_0^{z-1}M_1^{-z}$ ersetzen, können wir o.B.d.A. voraussetzen, daß $M_0=M_1=1$. Definieren wir
$$
f_n(z)\colon=f(z)e^{(z^2-1)/n},
$$
dann gilt mit $z=x+iy\in\cl S$: $\lim_{|z|\to\infty}f_n(z)=0$ sowie
$$
\sup_y\Vert f_n(iy)\Vert\leq e^{-1/n}
\quad\mbox{und}\quad
\sup_y\Vert f_n(1+iy)\Vert\leq\sup_ye^{-y^2/n}=1~.
$$
Nach dem Maximumprinzip folgt für alle $z\in S$: $\norm{f_n(z)}\leq1$. Da mit $n\to\infty$ die Funktionenfolge $f_n$ punktweise gegen $f$ konvergiert, folgt für alle $z\in S$: $\norm{f(z)}\leq1$.
$\eofproof$
Ersetzen wir $H$ durch $H+\e$, so können wir annehmen, daß $H > 0$, dann erfüllt die Funktion $f:\cl S\rar L(E)\simeq\Ma(n,\C)$, $f(z)\colon=H^zTH^{1-z}$ die Voraussetzungen des 3-Linien-Satz, denn für alle $y\in\R$ ist $H^{iy}$ eine Isometrie, also
$$
\Vert H^{iy}TH^{1-iy}\Vert=\Vert TH\Vert\leq1
\quad\mbox{und}\quad
\Vert H^{1+iy}TH^{-iy}\Vert=\Vert HT\Vert\leq1~.
$$
Mittels komplex differenzierbarer Abbildungen kann man Korollar auf verschiedenen Gebieten formulieren: Sei z.B. $F:S\rar\O$ komplex differenzierbar und auf $S\cup\pa S$ stetig mit $F(\pa S)\sbe\pa\O$. Für jede stetige Funktion $f:\O\cup\pa\O\rar X$, die auf $\O$ komplex differenzierbar ist, gilt für $f\circ F$ der 3-Linien-Satz unter den dortigen Voraussetzungen an $F\circ f$. Z.B. bildet $\exp$ den Streifen $S$ auf einen Kreisring ab und die Gerade $x+i\R$ bildet $\exp$ auf einen Kreis um $0$ mit dem Radius $e^x$ ab:
Minimum principle
$\proof$
Angenommen $f$ besitzt auf $B_r(w)$ keine Nullstelle, dann besitzt $f$ wegen $\inf\{|f(z)|:|z-w|=r\} > 0$ sowie der Stetigkeit auch in einer Umgebung $U$ von $\cl{B_r(w)}$ keine Nullstelle. Somit ist $g\colon=1/f$ auf $U$ komplex differenzierbar und es gilt: $|g(z_0)| > \sup\{|g(z)|:|z-w|=r\}$ - dies widerspricht jedoch dem Maximumprinzip.
$\eofproof$
Die Gebietstreue nicht konstanter, komplex differenzierbarer Funktionen folgt nun aus dem Minimumprinzip:
$\proof$
Da $f$ stetig und $\O$ zusammenhängend ist, ist $f(\O)$ zusammenhängend. Sei $z_0\in \O$ beliebig; da $f$ analytisch und nicht konstant ist, gibt es nach Lemma ein $r > 0$, so daß $\cl{B_r(z_0)}\sbe\O$ und für alle $z\in\pa B_r(z_0)$: $f(z)\neq f(z_0)=\colon w_0$. Damit ist
$$
2\e\colon=\inf\{|f(z)-w_0|:|z-z_0|=r\} > 0~.
$$
Für $w\in B_\e(w_0)$ betrachten wir die Funktion $f(z)-w$ auf $z\in\cl{B_r(z_0)}$; $|z-z_0|=r$ impliziert:
$$
|f(z)-w|
\geq|f(z)-w_0|-|w_0-w| > \e~.
$$
Andererseits ist $|f(z_0)-w|=|w-w_0| < \e$ und nach dem Minimumprinzip folgt, daß die Funktion $z\mapsto f(z)-w$ auf $B_r(z_0)$ eine Nullstelle besitzt, i.e.: $f(B_r(z_0))\spe B_\e(w_0)$.
$\eofproof$
Seien $U$ bzw. $V$ zwei offene, disjunkte, nicht leere Teilmengen von $\C$ und $f:U\cup V\rar\C$ die Abbildung $f|U=0$ und $f|V=1$. Dann ist $f$ komplex differenzierbar aber $f(U\cup V)=\{0,1\}$ ist keine offene Teilmenge von $\C$.
Eine stetige Abbildung $f$ eines metrischen Raumes $X$ in $\R$, die in einem Punkt $x_0$ ein lokales Maximum annimmt, kann nicht offen sein, denn falls für alle $x\in B_r(x_0)$ gilt: $f(x)\leq f(x_0)$, dann enthält $f(B_r(x_0))$ den Punkt $f(x_0)$ und ist selbst in $(-\infty,f(x_0)]$ enthalten, also kann $f(B_r(x_0))$ nicht offen sein.
$\proof$
Angenommen $f(D_r^c)$ ist nicht dicht, dann gibt es ein $w_0\notin f(D_r^c)$ und ein $\d > 0$, so daß für alle $z\notin D_r$: $|f(z)-w_0|\geq\d$; seien $z_1,\ldots,z_n$ die in ihrer Vielfachheit aufgelisteten Nullstellen von $f(z)-w_0$ in $D_r$, dann ist
$$
g(z)\colon=\frac{f(z)-w_0}{(z-z_1)\cdots(z-z_n)}
$$
eine nullstellenfreie, ganze Funktion, so daß für alle $z\notin D_r$: $|1/g(z)|\leq(C_0+C_1|z|^n)/\d$. Nach Korollar ist $1/g$ ein nullstellenfreies Polynom, i.e. $1/g$ ist konstant und damit ist $f$ ein Polynom.
$\eofproof$
Ist also $f:\C\rar\C$ eine ganze Funktion, so ist $f(\C)$ offen (nach Korollar) und dicht (nach Korollar); nach einem Satz von E. Picard (cf. e.g. wikipedia) enthält die Menge $f(\C)^c$ höchstens einen Punkt!
$\proof$
1. $f$ ist ein Polynom: $U\colon=f(D_1)$ ist nach Korollar offen und falls $f$ kein Polynom wäre, dann gäbe es nach Korollar ein $z\notin D_1$, so daß $f(z)\in U$, i.e. $f$ ist nicht injektiv.
2. Ist $f$ ein Polynom, so folgt aufgrund der Injektivität, daß $f$ nur eine einzige Nullstelle besitzt, also $f(z)=a(z-z_0)^n$ - dies Funktion ist aber nur dann injektiv, wenn $n=1$.
$\eofproof$
Convergence of sequences of holomorphic functions
Die folgende Proposition ist eine wesentliche Verschärfung von Proposition:
$\proof$
Ist $K\sbe B_r(w)$ kompakt, so gilt für alle $\z\in K$: $d(\z,\pa B_r(w))\geq\d > 0$ und damit nach dem Satz von Cauchy-Goursat mit $\g(t)=w+re^{2\pi it}$:
$$
\sup_{\z\in K}\norm{f_k^{(n)}(\z)-f_l^{(n)}(\z)}
\leq n!r\d^{-n-1}\int_0^1\norm{f_k(\g(t))-f_l(\g(t))}\,dt~.
$$
Nach dem Satz von der beschränkten Konvergenz (oder Satz) konvergieren sämtliche Ableitungen von $f_k:\O\rar X$ kompakt - nach Proposition ist damit $f$ beliebig oft komplex differenzierbar. Alternativ folgt auch für alle $r > 0$ und alle $w\in\O$ mit $B_r(w)\sbe\O$:
$$
f(w)=\frac1{2\pi i}\int_{\pa B_r(w)}\frac{f(z)}{z-w}\,dz
$$
i.e. $f$ ist komplex differenzierbar.
$\eofproof$
Hardy spaces $H_p(D)$
Sei $p\geq1$ und $H_p(D)$ der Raum
$$
H_p(D)\colon=\Big\{f:D\rar\C:\, f\mbox{ ist analytisch und }
\sup_{r < 1}\int|f(re^{it})|^p\,dt < \infty\Big\}~.
$$
Wir versehen diesen Raum mit der Norm
$$
\norm f_{H_p}\colon=\sup_{r < 1}\Big(
\frac1{2\pi}\int_0^{2\pi}|f(re^{it})|^p\,dt\Big)^{1/p}
$$
und zeigen, daß $H_p(D)$ ein Banachraum ist: Sei $f_n$ eine Cauchyfolge in $H_p(D)$ und $0 < r < r+s=R < 1$. Nach dem Satz von Cauchy-Goursat gilt:
$$
\forall z\in D_r:\quad
f(z)=\frac1{2\pi i}\int_{\pa D_R}\frac{f(w)}{w-z}\,dz~.
$$
Damit folgt aber für alle $z\in D_r$ wegen $p\geq1$:
\begin{eqnarray*}
|f_n(z)-f_m(z)|
&\leq&\frac{R}{2\pi s}\int_0^{2\pi}|f_n(re^{it})-f_m(re^{it})|\,dt\\
&\leq&\frac{R}{s}\Big(\frac1{2\pi}\int_0^{2\pi}|f_n(re^{it})-f_m(re^{it})|^p\,dt\Big)^{1/p}
\leq\frac{R}{s}\norm{f_n-f_m}_{H_p}
\end{eqnarray*}
und somit konvergiert $f_n$ kompakt.
Applications of the Residue Theorem
Computation of Residues
Zunächst einige Hinweise zur Berechnung von Residuen. In den meisten Fällen treffen wir folgende Situation an: gegeben seien zwei in einer Umgebung von $z_0\in\C$ komplex differenzierbare Funktionen $f,g$ mit $g^\prime(z_0)\neq0$ und $g(z_0)=0$. Dann folgt:
$$
\Res(z_0,f/g)=\frac{f(z_0)}{g^\prime(z_0)},
$$
denn unter diesen Voraussetzungen ist $h:z\mapsto(z-z_0)f(z)/g(z)$ in einer Umgebung von $z_0$ komplex differenzierbar mit $h(z_0)=f(z_0)/g^\prime(z_0)$, also gilt für hinreichend kleine $r >0$ mit $\g_r(t)=z_0+re^{it}$ nach dem Satz von Cauchy-Goursat oder der Cauchyschen Integralformel:
$$
\Res(z_0,f/g)
=\frac1{2\pi i}\int_{\g_r}\frac{f(z)}{g(z)}\,dz
=\frac1{2\pi i}\int_{\g_r}\frac{h(z)}{z-z_0}\,dz
=h(z_0)~.
$$
In diesem Fall ist $f(z)=z^2$ und $g=z^4-1$; da $g(1)=0$, $f(1)=1$ und $g^\prime(1)=4$, ist das gesuchte Residuum gleich $1/4$.
Für alle $w\in V\colon=f(B_r(z_0))$ besitzt die Funktion $g:z\mapsto zf^\prime(z)/(f(z)-w)$ auf $B_r(z_0)$ genau einen Pol, nämlich die Nullstelle $z_1$ des Nenners; da $\o(z_1,g)=-1$, folgt:
$$
\Res(z_1,g)=\frac{z_1f^\prime(z_1)}{f^\prime(z_1)}=z_1=f^{-1}(w)~.
$$
Falls allgemeiner $\o(z_0,f)=-m$ mit $m\in\N$, dann gibt es eine in einer Umgebung von $z_0$ komplex differenzierbaren Funktion $h$, so daß $f(z)=(z-z_0)^{-m}h(z)$, also:
$$
h(z)=\sum_{k=0}^\infty a_k(z-z_0)^k
\quad\mbox{und}\quad
f(z)=\sum_{k=0}^\infty a_k(z-z_0)^{k-m}
$$
Es gilt daher $\Res(z_0,f)=a_{m-1}$; nach der Taylor-Formel folgt:
\begin{equation}\label{arteq1}\tag{ART1}
\Res(z_0,f)=\frac1{(m-1)!}\frac{d^{m-1}}{dz^{m-1}}\Big|_{z=z_0}(z-z_0)^{m}f(z)
\end{equation}
Dasselbe Resultat erhält man auch unmittelbar aus dem Satz von Cauchy-Goursat oder der Cauchyschen Integralformel:
$$
\Res(z_0,f)
\colon=\frac1{2\pi i}\int_{\g_r}f(z)\,dz
=\frac1{2\pi i}\int_{\g_r}\frac{h(z)}{(z-z_0)^m}\,dz
=\frac1{(m-1)!}h^{(m-1)}(z_0)~.
$$
Da $\o(0,f)=-2$, also $m=2$, erhalten wir $\Res(0,f)$ durch einfache Ableitung der Funktion $h:z\mapsto(z/(e^z-1))^2$ im Punkt $z=0$, i.e. $\Res(0,f)=-1$.
Some Integrals
Nun zur Bestimmung von Integralen mithilfe des Residuensatzes: Sei $0 < x < 1$; wir möchten dann folgende reellen Intergale berechnen
$$
I(x)\colon=\int_\R\frac{e^{xt}}{e^t+1}\,dt
\quad\mbox{und}\quad
\int_\R\frac{te^{xt}}{e^t+1}\,dt
$$
Sei $C_n$ das in positiver Richtung umlaufene Rechteck mit den Eckpunkten $-n,n,n+2\pi i,-n+2\pi i$. Die Funktion $z\mapsto e^{xz}/(e^z+1)$ besitzt in diesem Rechteck nur den Pol $i\pi$ mit dem Residuum: $-e^{i\pi x}$, also für $n\to\infty$: $I(x)-I(x)e^{2i\pi x}=-2i\pi e^{i\pi x}$, oder:
$$
I(x)=\frac{\pi}{\sin(\pi x)}
\quad\mbox{und}\quad
\int_\R\frac{te^{xt}}{e^t+1}\,dt
=I^\prime(x)=-\frac{\pi^2\cos(\pi x)}{\sin^2(\pi x)}
$$
Bemerkungen: 1. Das zweite Integral kann man auf dieselbe Weise berechnen; Differentiation scheint aber einfacher zu sein!
2. Die Substitution $e^t=s$ ergibt $I(x)=\int_0^\infty\frac{s^{x-1}}{1+s}\,ds$, i.e. eine Mellin-Transformierte, cf \eqref{arteq9}.
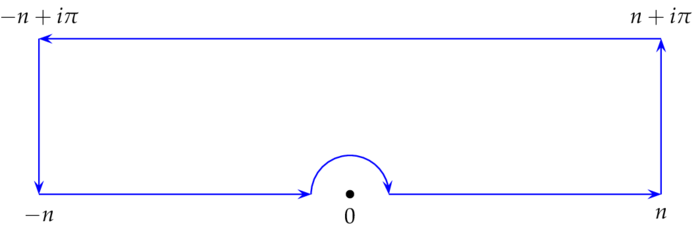
1. Sei $C_n$ das in positiver Richtung umlaufene Rechteck mit den Eckpunkten $-n,n,n+i\pi,-n+i\pi$. Die Funktion $z\mapsto ze^{xz}/(e^z-1)$ ist in diesem Rechteck komplex differenzierbar, also für $n\to\infty$:
$$
J(x)-\int_\R\frac{(t+i\pi)e^{xt+i\pi x}}{-e^t-1}\,dt=0~.
$$
Damit erhalten wir:
\begin{eqnarray*}
J(x)&=&-\cos(\pi x)\int_\R\frac{te^{xt}}{e^t+1}\,dt
+\pi\sin(\pi x)\int_\R\frac{e^{xt}}{e^t+1}\,dt\\
&=&-\cos(\pi x)I^\prime(x)+\pi\sin(\pi x)I(x)\\
&=&\left(\frac{\pi\cos(\pi x)}{\sin(\pi x)}\right)^2
+\pi^2
=\left(\frac{\pi}{\sin(\pi x)}\right)^2~.
\end{eqnarray*}
2. Wiederum betrachten wir den Integrationsweg $C_n$, nur diesmal ersetzen wir die Strecke $[-r,r]$, auf der die Singularität $0$ liegt, durch den in der oberen Halbebene liegenden Halbkreisbogen $\g_r(t)=re^{it}$, $t\in(0,\pi)$:
Da im Inneren von $C_n$ nun keine Singularität liegt, folgt nach dem Residuensatzes:
$$
0=\int_{-n}^{-r}+\int_{r}^{n}-\int_{\g_r}
+\int_{n}^{n+i\pi}+\int_{n+i\pi}^{-n+i\pi}-\int_{-n}^{-n+i\pi}
$$
Mit $n\to\infty$ und $r\to0$ konvergiert die Summe der beiden ersten Integrale gegen
$$
\pv\int_\R\frac{e^{xt}}{e^t-1}\,dt;
$$
das dritte konvergiert gegen
$$
\lim_{r\dar0}\int_{\g_r}\frac{ze^{xz}}{e^z-1}\frac1z\,dz
=\lim_{z\dar0}\frac{ze^{xz}}{e^z-1}i\pi
=i\pi,
$$
das fünfte gegen
$$
\int_\R\frac{e^{x(t+i\pi)}}{e^t+1}\,dt=\frac{\pi e^{i\pi x}}{\sin(\pi x)}
$$
und die verbleibenden zwei konvergieren gegen $0$.
The values of $\z(2k)$, $k\in\N$
Euler bestimmte diese Werte der Zetafunktion mithilfe der Produktdarstellung der Sinusfunktion \eqref{arteq16} (cf. Beispiel). Wir bestimmen sie hier über die Fourier-Reihen der Bernoulli-Polynome: Für $x\in\R$ und $z\in\C$ sei
$$
F(x,z)\colon=\frac{ze^{xz}}{e^z-1}
$$
vgl. Beispiel, dann ist $z\mapsto F(x,z)$ analytisch auf $\C\sm\{\pm2\pi in:n\in\N\}$, also können wir $z\mapsto F(x,z)$ um $0$ in eine Reihe entwickeln:
$$
F(x,z)
=\colon\sum_{k=0}^\infty\frac{B_k(x)}{k!}z^k~.
$$
Die Funktionen $B_k(x)$ sind tatsächlich Polynome $k$-ten Grades, die sogenannten Bernoulli-Polynome - die Zahlen $B_k\colon=B_k(0)$ nennt man Bernoulli-Zahlen und die Funktion $F(x,z)$ die erzeugende Funktion der Bernoulli-Polynome.
Zeigen Sie (Lösungsvorschlag)
- Der Konvergenzradius der Potenzreihe $\sum_k\frac{B_k(x)}{k!}z^k$ beträgt $2\pi$, also
$$
\limsup_k\frac{|B_k(x)|^{1/k}}k=\frac1{2e\pi}~.
$$
- $F(x,z)=e^{xz}F(0,z)$ und $B_n(x)$ ist ein Polynom
$n$-ten Grades mit dem führenden Koeffizienten $1$.
- $\pa_xF(x,z)=zF(x,z)$, $F(x+1,z)-F(x,z)=ze^{xz}$ und $F(1-x,z)=F(x,-z)$.
- $B_n^\prime(x)=nB_{n-1}(x)$, $B_n(x+1)-B_n(x)=nx^{n-1}$ und $B_n(1-x)=(-1)^nB_n(x)$.
- $B_1=-1/2$ und alle anderen Bernoulli-Zahlen zu ungeraden Indices verschwinden.
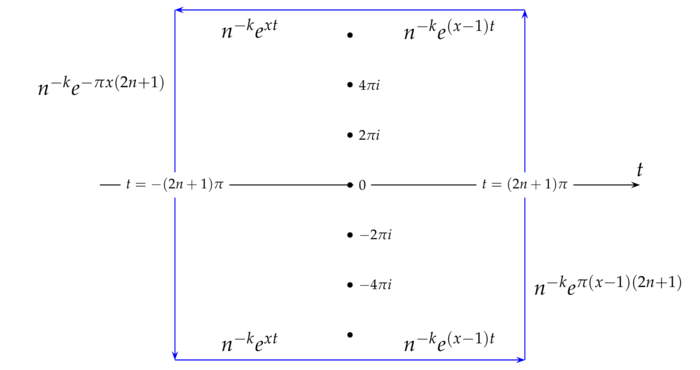
Seien nun $x\in[0,1)$, $k\geq2$ und $c_n$ der positiv (i.e. entgegen dem Uhrzeigersinn) umlaufene Rand des Quadrates mit den Eckpunkten $(2n+1)\pi(\pm1\pm i)$.
Auf dem Inneren des Quadrates hat die Funktion $z\mapsto z^{-k-1}F(x,z)$ die Pole $0,\pm2\pi i,\ldots,\pm2n\pi i$. Das Residuum bei $0$ ist $B_k(x)/k!$ und das bei $2m\pi i$, $m\neq0$, ist $(2m\pi i)^{-k}e^{2m\pi ix}$. Also erhalten wir nach dem Residuensatz:
$$
\int_{c_n}\frac{F(x,z)}{z^{k+1}}\,dz
=2\pi i\left(\frac{B_k(x)}{k!}
+\sum_{m=1}^n(2m\pi i)^{-k}e^{2m\pi ix}
+(-2m\pi i)^{-k}e^{-2m\pi ix}\right)~.
$$
Mit $n\to\infty$ konvergiert das Integral aber gegen $0$, d.h.:
\begin{eqnarray*}
B_k(x)
&=&-k!\sum_{m=1}^\infty
\frac{e^{2m\pi ix}}{(2m\pi i)^{k}}+\frac{e^{-2m\pi ix}}{(-2m\pi i)^{k}}\\
&=&-\frac{k!(1+(-1)^k)}{(2\pi i)^k}\sum_{m=1}^\infty\frac{\cos(2m\pi x)}{m^k}
-\frac{k!(1-(-1)^k)i}{(2\pi i)^k}\sum_{m=1}^\infty\frac{\sin(2m\pi x)}{m^k}~.
\end{eqnarray*}
Insbesondere für gerade bzw. ungerade Werte:
$$
B_{2k}(x)
=(-1)^{k+1}\frac{2(2k)!}{(2\pi)^{2k}}
\sum_{m=1}^\infty\frac{\cos(2m\pi x)}{m^{2k}}
\quad\mbox{bzw.}\quad
B_{2k+1}(x)
=(-1)^{k+1}\frac{2(2k+1)!}{(2\pi)^{2k+1}}\sum_{m=1}^\infty\frac{\sin(2m\pi x)}{m^{2k+1}}~.
$$
Dies sind also die Fourier-Reihen von $B_k\in L_2([0,1])$, $k=2,3,\ldots$; setzen wir $x=0$, so folgt:
$$
\forall k\in\N:\quad
\z(2k)=(-1)^{k+1}\frac{(2\pi)^{2k}B_{2k}}{2(2k)!}~.
$$
Z.B. $\z(2)=4\pi^2B_2/4=\pi^2/6$ und $\z(4)=-16\pi^4B_4/48=\pi^4/90$. Ob es eine ähnliche Formel für die Werte der Zetafunktion an den ungeraden Stellen gibt ist nach wie vor unbekannt, cf. e.g. wikipedia.
Bessel-Funktionen erster Art: Die Funktion
$$
F(x,z)\colon
=\exp(x(z-1/z)/2)
=e^{xz/2}e^{-x/2z}
=\colon\sum_{n\in\Z}J_n(x)z^n
$$
heißt die erzeugende Funktion der Bessel-Funktionen erster Art $J_n$, $n\in\Z$. Zeigen Sie:
- $F(-x,1/z)=F(x,z)=F(-x,-z)$ und $J_n(-x)=J_{-n}(x)=(-1)^nJ_n(x)$.
- Folgern Sie aus $2\pa_xF(x,z)=F(x,z)(z-z^{-1})$ und $2\pa_zF(x,z)=xF(x,z)(1+z^{-2})$: $2J_n^\prime=J_{n-1}-J_{n+1}$, $2nx^{-1}J_n(x)=J_{n-1}(x)+J_{n+1}(x)$ und $\ttd x(x^nJ_n(x))=x^nJ_{n-1}(x)$.
- Mit $\g(t)=e^{it}$ gilt für alle $n\in\Z$:
$$
J_n(x)
=\frac1{2\pi i}\int_\g\frac{\exp(x(z-1/z)/2)}{z^{n+1}}\,dz
=\frac1{2\pi}\int_0^{2\pi}e^{i(x\sin t-nt)}\,dt
=\Big(\frac{x}{2}\Big)^{n}\sum_{k=0}^\infty\frac{(-1)^k}{k!\G(n+k+1)}\Big(\frac{x}{2}\Big)^{2k}~.
$$
- Definieren wir $J_n$ durch letztere Reihe, so können wir $n\in\C$ wählen; zeigen Sie, daß dann die Besselsche Differentialgleichung gilt:
$$
\forall n\in\C:\quad
x^2J_n^\dprime(x)+xJ_n^\prime(x)+(x^2-n^2)J_n(x)=0~.
$$
modifizierte Bessel-Funktionen: Die Funktion
$$
F(x,z)
\colon=\exp(x(z+1/z)/2)
=\colon\sum_{n\in\Z}I_n(x)z^n
$$
hießt die erzeugende Funktion der modifizierten Bessel-Funktionen erster Art $I_n$, $n\in\Z$. Zeigen Sie:
- $F(x,1/z)=F(x,z)=F(-x,-z)$ und $I_n(-x)=I_{-n}(-x)=(-1)^nI_n(x)$.
- Folgern Sie aus $2\pa_xF(x,z)=F(x,z)(z+z^{-1})$ und $2\pa_zF(x,z)=xF(x,z)(1-z^{-2})$: $2I_n^\prime=I_{n-1}+I_{n+1}$, $2nx^{-1}I_n(x)=I_{n-1}(x)-I_{n+1}(x)$ und $\ttd x(x^nI_n(x))=x^nI_{n-1}(x)$.
- Mit $\g(t)=e^{it}$ gilt für alle $n\in\Z$:
$$
I_n(x)
=\frac1{2\pi i}\int_\g\frac{\exp(x(z+1/z)/2)}{z^{n+1}}\,dz
=\frac1{2\pi}\int_0^{2\pi}e^{x\cos t-nit}\,dt
=\Big(\frac{x}{2}\Big)^{n}\sum_{k=0}^\infty\frac{1}{k!\G(n+k+1)}\Big(\frac{x}{2}\Big)^{2k}~.
$$
- Definieren wir $I_n$ durch letztere Reihe, so können wir $n\in\C$ wählen; zeigen Sie, daß dann die modifizierte Besselsche Differentialgleichung gilt:
$$
\forall n\in\C:\quad
x^2I_n^\dprime(x)+xI_n^\prime(x)-(x^2+n^2)I_n(x)=0~.
$$
Perron`s formula and the distribution of primes
Sei $f:\N\rar\C$ eine Funktion, so daß die Dirichlet-Reihe
$$
\sum_{n=1}^\infty f(n)n^{-z}
$$
von $f$ absolut konvergiert, dann folgt mittels der Abelschen Summationsformel:
$$
\sum_{n=1}^\infty f(n)n^{-z}
=z\int_1^\infty\Big(\sum_{n\leq x}f(n)\Big)x^{-z-1}\,dx~.
$$
Die Perronsche Formel ist die dazu inverse Beziehung, d.h. aus der Kenntnis der Reihe $\sum f(n)n^{-z}$ gestattet sie die Partialsummen $\sum_{n\leq x}f(n)$ zu berechnen. Wir benötigen hierzu einen einfachen Hilfssatz: Sei $a > 0$, $c:\R\rar\C$ die Kurve $c(t)=a+it$, dann gilt für alle $b > 0$:
$$
\frac1{2\pi i}\int_c z^{-1}b^z\,dz
=\left\{
\begin{array}{cl}
0&\mbox{falls $0 < b < 1$}\\
1&\mbox{falls $1 < b$}
\end{array}
\right.
$$
Die Funktion $f:z\mapsto z^{-1}b^z$ ist auf $\C\sm\{0\}$ komplex differenzierbar; sei $c_n$ der Rand des Rechtecks mit den Eckpunkten $a-in,a+in,a+n+in$ und $a+n-in$. Für $0 < b < 1$ verschwinden die Integrale über die drei Seiten $[a+in,a+n+in]$, $[a+n+in,a+n-in]$ und $[a+n-in,a-in]$ mit $n\to\infty$, also folgt in diesem Fall die Behauptung nach der Cauchyschen Integralformel.
Falls $b > 1$, so sei $c_n$ der Rand des Rechtecks mit den Eckpunkten $a-in,a+in,a-n+in$ und $-a-n-in$. Wiederum verschwinden die Integrale über die drei Seiten $[a+in,a-n+in]$, $[a-n+in,a-n-in]$ und $[a-n-in,a-in]$ mit $n\to\infty$. Da $\Res(f,0)=1$, folgt in diesem Fall die Behauptung nach dem Residuensatz.
Konvergiert nun die Reihe $\sum f(n)n^{-z}$ absolut, so gilt die Perronsche Formel
\begin{equation}\label{arteq2}\tag{ART2}
\sum_{n\leq x}f(n)
=\frac1{2\pi i}\int_c\Big(\sum_{n=1}^\infty f(n)n^{-z}\Big)z^{-1}x^z\,dz
\end{equation}
wobei $c:\R\rar\C$ eine Kurve $c(t)=a+it$ mit $a >0$ bezeichnet und $x\in\R^+$ keine ganze Zahl ist. Dies folgt unmittelbar aus dem obigen Hilfssatz, denn $\int_c z^{-1}(x/n)^z\,dz=1$ für $1 < x/n$ und $\int_c z^{-1}(x/n)^z\,dz=0$ für $1 > x/n$.
Eine der bekanntesten Anwendungen der Perronschen Formel betrifft den Zusammenhang zwischen der Primzahlverteilung und der Zetafunktion, die wir genauer in Abschnitt untersuchen.
Für $x > 0$, $x\notin\N$ und $\psi(x)\colon=\sum_{n\leq x}\L(n)$ erhalten wir nach der Perronsche Formel:
$$
\frac{\psi(x)}{x}
=\frac1{2\pi i}\int_c\Big(\sum_{n=1}^\infty\L(n)n^{-z}\Big)z^{-1}x^{z-1}\,dz
=\frac1{2\pi i}\int_c\frac{\z^\prime(z)}{\z(z)z}x^{z-1}\,dz~.
$$
Sei nun $\pi(x)$ die Anzahl der Primzahlen $\leq x$, dann gilt (cf. Abschnitt):
$$
\lim_{x\to\infty}\frac{\pi(x)}{\frac x{\log x}}=a
\quad\mbox{falls}\quad
\lim_{x\to\infty}\frac{\psi(x)}x=a~.
$$
Gaussian integral
Nahezu alle Berechnungen des Integrals $\int e^{-x^2}\,dx$ beruhen darauf, das Integral in mehr oder minder versteckter Form mit sich selbst zu multiplizieren; eine Alternative ist folgende (cf. H. Kneser, Funktionentheorie): Sei $\Re a\neq0$, $\Im a > 0$ und
$$
h(z)\colon=\frac{e^{-z^2}}{1-e^{-(2az+a^2)}}~.
$$
Der Nenner verschwindet genau dann, wenn $z=-a/2+n\pi i/a$, $n\in\Z$. Besitzt $h$ auf dem Rand des Streifen $S=[0\leq\Im z\leq\Im a]$ keinen Pol, so gilt nach dem Residuensatz:
$$
2\pi i\sum_{w\in S}\Res(w,h)=\int_\R h(z)-h(z+a)\,dz~.
$$
Der Nenner von $h$ ist genau dann periodisch mit der Periode $a$, wenn $2a^2$ ein Vielfaches von $2\pi i$ ist; in diesem Fall erhalten wir
$$
h(z)-h(z+a)
=\frac{e^{-z^2}-e^{-(a+z)^2}}{1-e^{-(2az+a^2)}}
=\frac{e^{-z^2}(1-e^{-(2az+a^2)})}{1-e^{-(2az+a^2)}}
=e^{-z^2}~.
$$
Setzen wir nun $a=(1+i)\sqrt{\pi/2}$, so folgt $2a^2=2\pi i$ und $h$ besitzt in $S$ nur den Pol $z=a/2$; das Residuum an dieser Stelle berechnet sich zu:
$$
\frac{e^{-a^2/4}}{2ae^{-2a^2}}
=\frac{e^{-a^2/4}}{2a}
=\frac{e^{-i\pi/4}}{\sqrt{2\pi}(1+i)}
=\frac{1}{2\sqrt\pi}\frac{1-i}{1+i}
=-\frac{i}{2\sqrt\pi}~.
$$
Es folgt:
$$
\int_\R e^{-z^2}\,dz
=\int_\R h(z)-h(z+a)\,dz
=-\frac{2\pi i^2}{2\sqrt\pi}
=\sqrt\pi~.
$$
Residues at infinity
Sei $E$ eine endliche Teilmenge von $\C$ und $f:\C\sm E\rar X$ komplex differenzierbar. Unter dem Residuum im Unendlichen $\Res(\infty,f)$ von $f$ versteht man das Residuum
$$
\Res(\infty,f)\colon=\Res(0,-f(R^2/z)R^2/z^2),
$$
wobei $R > 0$ so zu wählen ist, daß $E\sbe D_R$. Setzen wir $F(z)\colon=R^2/z$ und $\g(t)=Re^{it}$, $t\in(-\pi,\pi)$, dann ist $F\circ\g(t)=Re^{-it}=\g^{-1}(t)$, also:
\begin{eqnarray*}
2\pi i\sum_{w\in E}\Res(w,f)
&=&\int_\g f(z)\,dz
=-\int_{F\circ\g}f(z)\,dz\\
&=&\int_\g f(R^2/z)R^2/z^2\,dz
=-2\pi i\Res(\infty,f)
\end{eqnarray*}
Schließt man also das Residuum im Unendlichen mit ein, so ist die Summe aller Residuen gleich Null!
Integrals: type 1
Sei $H^+\colon=\{z\in\C:\Im z > 0\}$ die oberen Halbebene, $E$ eine endliche Teilmenge von $H^+$, $f:H^+\sm E\rar X$ komplex differenzierbar und auf $\cl{H^+}\sm E$ stetig, so daß
$$
\lim_{z\to\infty,z\in\cl{H^+}}z f(z)=0~.
$$
Dann gilt:
\begin{equation}\label{arteq3}\tag{ART3}
\lim_{n\to\infty}\int_{-n}^n f(t)\,dt
=2\pi i\sum_{z\in E}\Res(z,f)~.
\end{equation}
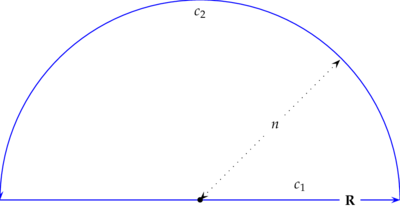
Ist $c_1$ die Strecke von $-n$ nach $n$ und $c_2$ der positiv durchlaufene Halbkreis von $n$ nach $-n$, so folgt die Behauptung aus
$$
\limsup_n\Big|\int_{c_2}f(z)\,dz\Big|
\leq\pi\limsup_n\sup\{|nf(ne^{it})|:0\leq t\leq\pi\}=0
$$
sowie dem Residuensatz.
Da $m\geq1$, folgt: $\lim_{z\to\infty}z(1+z^{2m})^{-1}=0$ und damit:
\begin{eqnarray*}
\int_\R\frac{1}{1+t^{2m}}\,dt
&=&2\pi i\sum_{z^{2m}=-1,\Im z > 0}\frac1{2mz^{2m-1}}\\
&=&-\frac{\pi i}m\sum_{k=0}^{m-1}e^{(2k+1)\pi i/2m}
=-\frac{2\pi ie^{\pi i/2m}}{m(1-e^{\pi i/m})}
=2\frac{\frac{\pi}{2m}}{\sin\frac{\pi}{2m}}~.
\end{eqnarray*}
Integrals: type 2a
Sei $E$ eine endliche Teilmenge von $\C\sm\R_0^+$. Ist $f:\C\sm E\rar X$ komplex differenzierbar, so daß
$$
\lim_{z\to0,z\in\C\sm\R_0^+}zf(z)\Log z
=\lim_{z\to\infty,z\in\C\sm\R_0^+}zf(z)\Log z
=0,
$$
wobei $\Log z\colon=\log|z|+i\arg(z)$ mit $0\leq\arg(z) < 2\pi$. Dann gilt:
\begin{equation}\label{arteq4}\tag{ART4}
\lim_{n\to\infty}\int_0^n f(t)\,dt
=-\sum_{z\in E}\Res(z,f(z)\Log z)~.
\end{equation}
$\Log:\C\sm\R_0^+\rar\C$ ist komplex differenzierbar und
$$
\forall t > 0:\quad
\lim_{\e\dar0}\Log(t+i\e)=\log t
\quad\mbox{und}\quad
\lim_{\e\dar0}\Log(t-i\e)=\log t+2\pi i~.
$$
Sei $c_1$ die Strecke von $i\e$ nach $n+i\e$, $c_2$ der positiv durchlaufene Kreis von $n+i\e$ nach $n-i\e$, $c_3$ die Strecke von $n-i\e$ nach $-i\e$ und $c_4$ der negativ durchlaufene Kreis von $-i\e$ nach $i\e$.
Nach dem Residuensatz ist
$$
2\pi i\sum_{z\in E}\Res(z,f(z)\Log z)
=\lim_{n\to\infty}\lim_{\e\dar0}\int_{c_1c_2c_3c_4}f(z)\Log z\,dz~.
$$
Da nach Voraussetzung $\lim_{\e\dar0}\int_{c_4}f(z)\Log z\,dz=\lim_{n\to\infty}\int_{c_2}f(z)\Log z\,dz=0$
und
\begin{eqnarray*}
\lim_{\e\dar0}\int_{c_3}f(z)\Log z\,dz
&=&-\int_0^n f(t)(\log t+2\pi i)\,dz\\
&=&-2\pi i\int_0^n f(t)\,dt
-\lim_{\e\dar0}\int_{c_1}f(z)\Log z\,dz
\end{eqnarray*}
folgt die behauptete Beziehung.
Da $m\geq1$, folgt: $\lim_{z\to\infty}z(1+z^{2m+1})^{-1}\log z=0$; mit $a\colon=e^{\pi i/2m+1}$ sind die Nullstellen von $1+z^{2m+1}$ gleich: $a,a^3,\ldots,a^{4m+1}$, also erhalten wir:
\begin{eqnarray*}
\int_0^\infty\frac{1}{1+t^{2m+1}}\,dt
&=&-\sum_{z^{2m+1}=-1}\frac{\Log z}{(2m+1)z^{2m}}\\
&=&\frac{\pi i}{(2m+1)^2}\sum_{k=0}^{2m}(2k+1)a^{2k+1}~.
\end{eqnarray*}
Nun ist aber für alle $z\in\C$:
$$
\sum_{k=0}^{2m}(2k+1)z^{2k+1}
=z\ftd z\sum_{k=0}^{2m}z^{2k+1}
=z\ftd z\Big(z\frac{1-z^{4m+2}}{1-z^2}\Big);
$$
also wegen $a^{4m+2}=1$ und $(1/a-a)/2i=-\sin(\pi/(2m+1))$:
$$
\int_0^\infty\frac{1}{1+t^{2m+1}}\,dt
=-\frac{\pi i}{(2m+1)^2}\frac{4m+2}{1/a-a}
=\frac{\pi}{(2m+1)\sin(\pi/(2m+1))}~.
$$
Integrales: type 2b
Durch Integration der Funktion $f(z)\Log^2z$ erhält man analog für eine auf $\C\sm E$, $E\sbe\C\sm\R_0^+$, komplex differenzierbare Funktion $f$ mit
$$
\lim_{z\to0}z\Log^2zf(z)
=\lim_{z\to\infty}z\Log^2zf(z)
=0
$$
folgende Beziehung:
\begin{equation}\label{arteq5}\tag{ART5}
\lim_{n\to\infty}\int_0^n f(t)\log t\,dt
=-i\pi\int_0^\infty f(t)\,dt-\tfrac12\sum_{z\in E}\Res(z,f(z)\Log^2z)~.
\end{equation}
Integrales: trigonometric integrals
Sei $R:[-1,1]^2\rar\C$, so daß
$$
\wt R(z)\colon=R(\tfrac12(z+1/z),\tfrac1{2i}(z-1/z))/z
$$
auf $\pa D$ keine Singularitäten besitzt und auf $D$ mit Ausnahme endlich vieler Punkte $E$ komplex differenzierbar ist. Dann gilt
\begin{equation}\label{arteq6}\tag{ART6}
\int_{-\pi}^\pi R(\cos t,\sin t)\,dt
=2\pi\sum_{z\in E}\Res(z,\wt R)
\end{equation}
Denn ist $\g:(-\pi,\pi]\rar\C$ die Kurve $\g(t)=e^{it}$, so gilt:
$$
i\int_{-\pi}^\pi R(\cos t,\sin t)\,dt
=\int_\g\wt R(z)\,dz~.
$$
In diesem Fall ist
$$
\wt R(z)
=\frac1{z(1-a(z+1/z)+a^2)}
=\frac{-1}{a(z-a)(z-1/a)}
$$
und $\Res(a,\wt R)=1/(1-a^2)$ bzw. $\Res(1/a,\wt R)=1/(a^2-1)$.
Integrales: Fourier transforms
Sei $E\sbe H^+\colon=[\Im z > 0]$ endlich, $U$ eine Umgebung von $H^+$ und $f:U\sm E\rar X$ komplex differenzierbar, so daß:
$$
\lim_{z\to\infty,z\in H^+}f(z)=0,
$$
dann gilt:
\begin{equation}\label{arteq7}\tag{ART7}
\forall y < 0:\quad
\lim_{n\to\infty}\int_{-n}^n f(t)e^{-iyt}\,dt
=2\pi i\sum_{z\in E}\Res(z,f(z)e^{-iyz})~.
\end{equation}
Sei $c_n$ der rechteckige Weg mit die Eckpunkten $-n$, $n$, $n+in$ und $-n+in$.
Nach Voraussetzung gilt dann
$$
\lim_n\int_{n}^{n+in}f(z)e^{-iyz}\,dz
=\lim_n\int_{n+in}^{-n+in}f(z)e^{-iyz}\,dz
=\lim_n\int_{-n+in}^{-n}f(z)e^{-iyz}\,dz
=0~.
$$
Somit folgt die Behauptung aus dem Residuensatz.
Für $y < 0$ ist das Integral gleich
$$
2\pi i\Res(i,(1+z^2)^{-1}e^{-izy})
=2\pi i e^{y}/2i
=\pi e^{y}
$$
und für $y > 0$ verlegt man den Integrationsweg entweder in die untere Halbebene oder man beachtet, daß die Funktion $t\mapsto(1+t^2)^{-1}$ reell und symmetrisch ist (vgl. Beispiel).
Integrals: Laplace transforms
Sei $E\sbe\O\colon=[\Re z > 0,\Im z > 0]$ endlich, $U$ eine Umgebung von $[\Re z\geq0,\Im z\geq0]$ und $f:U\sm E\rar X$ komplex differenzierbar, so daß:
$$
\lim_{z\to\infty,z\in\O}f(z)=0,
$$
dann gilt für alle $x > 0$ (vgl. Unterabschnitt):
\begin{equation}\label{arteq8}\tag{ART8}
\lim_n\int_0^n f(t)e^{-xt}\,dt-i\int_0^{n}f(it)e^{-ixt}\,dt
=2\pi i\sum_{z\in E}\Res(z,f(z)e^{-xz})~.
\end{equation}
Bezeichnet $c_n$ die Strecke von $n$ nach $n+in$ gefolgt von der Strecke von $n+in$ nach $in$, so wählen wir zu $\e > 0$ $n\in\N$ so groß, daß für alle $|z|\geq n$: $|f(z)|\leq\e$. Dann erhalten wir
$$
\Big|\int_{c_n}f(z)e^{-xz}\,dz\Big|
\leq\e ne^{-xn}+\e\int_0^{n}e^{-xt}\,dt
\leq\e ne^{-xn}+\e/x~.
$$
Die Beziehung \eqref{arteq8} folgt nun aus dem Residuensatz angewandt auf die Funktion $f(z)e^{-xz}$ und den rechteckigen geschlossenen Integrationsweg von $0$ nach $n$ nach $n+in$ nach $in$ und zurück zu $0$ mit $n\to\infty$.
Die Funktion $f:z\mapsto z^{a-1}$ ist auf $\O\colon=[\Im z > 0,\Re z > 0]$ komplex differenzierbar und es gilt: $\lim_{z\to\infty}f(z)=0$; also:
$$
\lim_n\int_0^n t^{a-1}e^{-xt}\,dt-\lim_n \int_0^{n}(it)^{a-1}e^{-ixt}i\,dt=0
$$
Das erste Integral konvergiert gegen $\G(a)x^{-a}$ und das zweite gegen $e^{ia\pi/2}\int_0^{n}t^{a-1}e^{-ixt}\,dt$.
Integrals: Mellin transforms
Sei $E$ eine endliche Teilmenge von $\C\sm\R_0^+$ und $a\in\C$. Ist $f:\C\sm E\rar X$ komplex differenzierbar, so daß
$$
\lim_{z\to0,z\in\C\sm\R_0^+}z^af(z)=0
\quad\mbox{und}\quad
\lim_{z\to\infty,z\in\C\sm\R_0^+}z^af(z)=0,
$$
dann gilt:
\begin{equation}\label{arteq9}\tag{ART9}
\lim_{n\to\infty}\int_0^n f(t)t^{a-1}\,dt
=\frac{2\pi i}{1-e^{2\pi ia}}\sum_{z\in E}\Res(z,f(z)z^{a-1})
\end{equation}
wobei $z^{a-1}=\exp((a-1)\Log z)$ und $\Log z$ wie in Typ 2a definiert ist. Die Funktion $F(a)\colon=\int_0^\infty f(t)t^{a-1}\,dt$ heißt die Mellin-Transformierte von $f$. Cf. e.g. wikipedia. Seien $c_1,c_2,c_3,c_4$ wie in Typ 2a, dann folgt nach Voraussetzung:
$$
\lim_{n\to\infty}\lim_{\e\dar0}\int_{c_2}f(z)z^{a-1}\,dz=0
\quad\mbox{und}\quad
\lim_{\e\dar0}\int_{c_4} f(z)z^{a-1}\,dz=0~.
$$
Da ferner für alle $t > 0$:
$$
\lim_{\e\dar0}(t+i\e)^{a-1}=t^{a-1}
\quad\mbox{und}\quad
\lim_{\e\dar0}(t-i\e)^{a-1}=t^{a-1}e^{2\pi ia}
$$
erhalten wir weiters
\begin{eqnarray*}
\lim_{\e\dar0}\int_{c_1}f(z)z^{a-1}\,dz
&=&\int_0^n f(t)t^{a-1}\,dt
\quad\mbox{und}\\
\lim_{\e\dar0}\int_{c_3}f(z)z^{a-1}\,dz
&=&-e^{2\pi ia}\int_0^n f(t)t^{a-1}\,dt~.
\end{eqnarray*}
und \eqref{arteq9} folgt wiederum aus dem Residuensatz.
Für alle $0 < x < 1$ gilt (cf. Beispiel):
$$
\b(x,1-x)
=\int_0^\infty\frac{t^{x-1}}{t+1}\,dt
=\frac{\pi}{\sin(\pi x)}~.
$$
Es folgt die Ergänzungsformel der Gammafunktion \eqref{arteq17}:
$$
\forall 0 < x < 1:\quad
\frac1{\G(x)\G(1-x)}=\frac{\sin(\pi x)}{\pi}~.
$$
Das Residuum bei $z=-1$ ist $(-1)^{x-1}=\exp((x-1)\Log(-1))=e^{i\pi(x-1)}$, also:
$$
\b(x,1-x)=\frac{-2\pi ie^{i\pi x}}{1-e^{2\pi ix}}
=\frac{2\pi i}{-e^{-i\pi x}+e^{i\pi x}}
=\frac{\pi}{\sin(\pi x)}~.
$$
Z.B. erhalten wir für die Mellin-Transformierte von $f(x)=e^{-wx^p}$ mit $p > 0$ und $\Re w > 0$ nach Beispiel: $Mf(z)=\G((z+1)/p)w^{(-z-1)/p}/p$ und diese Funktion besitzt für kein $z\in i\R$ eine Nullstelle.
Integrals: type 2c
Analog erhalten wir wiederum für eine auf $\C\sm E$, $E\sbe\C\sm\R_0^+$ isoliert, komplex differenzierbare Funktion $f$ unter den Voraussetzungen
$$
\lim_{z\to0,z\in\C\sm\R_0^+}z^a\Log zf(z)=0
\quad\mbox{und}\quad
\lim_{z\to\infty,z\in\C\sm\R_0^+}z^a\Log zf(z)=0~:
$$
\begin{equation}\label{arteq10}\tag{ART10}
\lim_{n\to\infty}
\Big(\int_0^n f(t)t^{a-1}\log t\,dt
-\frac{2\pi ie^{2\pi ia}}{1-e^{2\pi ia}}\int_0^n f(t)t^{a-1}\,dt\Big)
=\frac{2\pi i}{1-e^{2\pi ia}}\sum_{z\in E}\Res(z,f(z)z^{a-1}\Log z)~.
\end{equation}
I.A. ist folgende Alternative einfacher: Sei $F(a)\colon=\int_0^\infty f(t)t^{a-1}\,dt$, dann gilt:
$$
\int_0^\infty f(t)t^{a-1}\log^n t\,dt=F^{(n)}(a)~.
$$
Achtung: Dies setzt voraus, daß die Funktionen $t\mapsto f(t)t^{a-1}\log^k t$ für alle $k=0,\ldots,n$ über $\R^+$ integrierbar sind!
1. Ein Sonderfall von Beispiel.
2. Sei $F(x)\colon=\int_0^\infty\frac{t^{x-1}}{1+t^2}\,dt$; mit der Substitution $t^2\to s$ erhalten wir nach Beispiel:
$$
F(x)=\tfrac12\int_0^\infty\frac{s^{x/2-1}}{1+s}\,ds
=\frac{\pi}{2\sin(\pi x/2)}
$$
und die behauptete Beziehung folgt nach Differentiation.
1. Mithilfe der oben definierten Funktion $F$:
$$
\int_0^\infty\frac{t^{-1/2}\log t}{1+t^2}\,dt
=F^\prime(1/2)
=-\frac{\pi^2\cos(\pi/4)}{4\sin^2(\pi/4)}
=-\sqrt2(\pi/2)^2~.
$$
2. Für $f(z)\colon=1/(1+z^2)$ und $a=1/2$, folgt nach \eqref{arteq10}:
$$
I=-\pi i\int_0^n f(t)t^{-1/2}\,dt
+\pi i\sum_{z=\pm i}\Res(z,f(z)z^{-1/2}\Log z)
$$
Das Residuum bei $i$ ist $i^{-1/2}\Log(i)/2i=e^{-i\pi/4}\pi/4$ und das Residuum bei $-i$ ist $(-i)^{-1/2}\Log(-i)/-2i=-e^{-3i\pi/4}3\pi/4$.
Integrals of the form $\int_0^\infty f(t^x)\,dt$, $x > 1$
Diese Integrale kann man u.A. durch Integration entlang des Randes eines Sektors mit dem Öffnungswinkel $2\pi/x$ bestimmen, i.e. $S\colon=\{z\in\C:0 < \arg(z) < 2\pi/x\}$: Ist $E\sbe S$ endlich, $F:S\sm E\rar\C$, $F(z)\colon=f(z^x)$ komplex differenzierbar und auf $\cl S\sm E$ stetig, so daß
$$
\lim_{z\to\infty,z\in S} zF(z)=0~.
$$
Dann gilt mit $z^x=\exp(x\Log z)$, $\Log z\colon=\log|z|+i\arg(z)$ und $\arg(z)\in[0,2\pi)$:
$$
\lim_{n\to\infty}\int_0^n f(t^x)\,dt
=\frac{2\pi i}{1-e^{2\pi i/x}}\sum_{z\in E}\Res(z,F)~.
$$
Denn nach dem Residuensatz folgt für $E\sbe D_n$:
$$
\lim_{n\to\infty}\int_0^nf(t^x)\,dt
+\lim_{n\to\infty}\int_{\g_n}F(z)\,dz
-e^{2\pi i/x}\lim_{n\to\infty}\int_0^nf(t^x)\,dt
=2\pi i\sum_{z\in E}\Res(z,F)
$$
wobei $\g_n$ den Kreisbogen des Radius` $n$ mit dem Innenwinkel $2\pi/x$ bezeichnet. Die Voraussetzungen implizieren nun, daß der zweite Limes verschwindet.
Da sowohl die rechte als auch die linke Seite auf $\Re w > 1$ analytisch sind (cf. Beispiel), genügt es die Beziehung für $w=x\in(1,\infty)$ zu zeigen.
1. Ein Sonderfall von Beispiel.
2. Die Funktion $g(z)=1+z^x$ besitzt auf dem Sektor $[0 < \arg(z) < 2\pi/x]$ nur im Punkt $z_0\colon=e^{i\pi/x}$ eine Nullstelle; da $g^\prime(z_0)\neq0$ folgt:
$$
\Res(z_0,1/g)
=\frac1{g^\prime(z_0)}
=\frac1{xz_0^{x-1}}
=\frac1{xe^{i\pi(x-1)/x}}
=-\frac1{xe^{-i\pi/x}}~.
$$
Damit erhalten wir
$$
I(x)
=-\frac{2\pi i}{(1-e^{2\pi i/x})xe^{-i\pi/x}}
=-\frac{2\pi i}{x(e^{-\pi i/x}-e^{\pi i/x})}
=\frac{\pi/x}{\sin(\pi/x)}~.
$$
Fourier transform of gaussian measures
Sei $\g_t$ das Gaußmaß auf $\R$ mit der Varianz $2t > 0$, d.h.
$$
\g_t(dx)
=p(t,x)\,dx
=(4\pi t)^{-1/2}\exp(-x^2/4t)\,dx~.
$$
Dann ist die Fourier-Transformierte des Gaußmaßes
$$
\wh\g_t(y)
\colon=\frac1{\sqrt{2\pi}}\int e^{-ixy}\,\g_t(dx)
\quad\mbox{gegeben durch}\quad
\wh\g_t(y)=\frac1{\sqrt{2\pi}}e^{-ty^2}~.
$$
Die Fourier-Transformierte macht aber auch für komplexe Werte des Parameters $w$ Sinn:
\begin{equation}\label{arteq11}\tag{ART11}
\forall \Re w > 0\,\forall y\in\C:\quad
\wh\g_w(y)=\frac1{\sqrt{2\pi}}e^{-wy^2}~.
\end{equation}
1. Sei $w=t > 0$: dies ist ein spezieller Fall von Proposition. Quadratische Ergänzung ergibt:
$$
-izy-z^2/4t=-(z+2ity)^2/4t-ty^2~.
$$
Sei nun $c_n$ der geschlossene Weg von $-n$ nach $n$ nach $n-2ity$ nach $-n-2ity$ und zurück nach $-n$, dann konvergieren die Integrale über die Strecken von $n$ nach $n-2ity$ und von $-n-2ity$ nach $-n$ gegen $0$; also folgt nach der Cauchyschen Integralformel:
\begin{eqnarray*}
0
&=&\lim_n\int_{c_n}e^{-izy}e^{-z^2/4t}\,dz\\
&=&\lim_n\int_{-n}^ne^{-ixy}e^{-x^2/4t}\,dx
+\lim_n\int_{n-2ity}^{-n-2ity}e^{-(z+2ity)^2/4t-ty^2}\\
&=&\int_\R e^{-ixy}e^{-x^2/4t}\,dx-e^{-ty^2}\int_\R e^{-x^2/4t}\,dx
=\sqrt{2\pi}\sqrt{4\pi t}\,\wh\g_t(y)-\sqrt{4\pi t}\,e^{-ty^2}~.
\end{eqnarray*}
2. Schließlich sind sowohl die linke als auch die rechte Seite von \eqref{arteq11} auf $[\Re w > 0]$ komplex differenzierbar, also analytisch auf $[\Re w > 0]$ und somit folgt die behauptete Gleichheit aus 1. sowie dem Identitätssatz. Vgl. Unterabschnitt.
Nach dem Wiener Theorem erhalten wir daher z.B.:
Singular integrals over $\R^+$
Besitzt die Funktion $f$ auf dem Integrationsweg Pole, so nimmt man anstelle des Integrals dessen Cauchyschen Hauptwert:
Wiederum setzen wir $z^{x-1}=\exp((x-1)\Log z)$ mit $\Log z\colon=\log|z|+i\arg(z)$ und $\arg(z)\in[0,2\pi)$. Sei $\g(t)=1+re^{it}$, $t\in(0,2\pi)$, dann gilt:
$$
0=(1-e^{2\pi i(x-1)})I(x)
-\lim_{r\dar0}\int_{\g}\frac{z^{x-1}}{z-1}\,dz~.
$$
Achtung: die Funktion $z\mapsto z^{x-1}$ ist im Inneren von $\g$ weder stetig noch meromorph!
Da mit $r\dar0$: $\g(t)^{x-1}\to1$ für $\Im\g(t) > 0$ und $\g(t)^{x-1}\to e^{2\pi ix}$ für $\Im\g(t) < 0$, folgt:
$$
\lim_{r\dar0}\int_{\g}\frac{z^{x-1}}{z-1}\,dz
=i\pi(1+e^{2\pi i x})
$$
und damit:
$$
I(x)
=i\pi\frac{1+e^{2\pi i x}}{1-e^{2\pi i x}}
=-\pi\cot(\pi x)~.
$$
Singular integrals over $\R$
Anders als im voranstehenden Beispiele gestaltet sich hier die Bestimmung der Hauptwerte meist ein wenig komplizierter: die Beiträge an den reellen Polen zählen im einfachsten Fall nur zur Hälfte (cf. Beispiel oder Beispiel).
Wir demonstrieren dies an zwei Beispielen: 1. Die (distributionelle) Fourier-Transformierte der Funktion $1/(x^2-a^2)$ für $a > 0$:
$$
\pv\int_\R\frac{e^{ixy}}{x^2-a^2}\,dx=-\pi\sign(y)\frac{\sin(ay)}a~.
$$
Sei $\g_+(t)\colon=a+re^{it}$, $t\in(0,\pi)$, dann folgt:
$$
\lim_{r\dar0}\int_{\g_+}\frac{e^{izy}}{z^2-a^2}\,dz
=\lim_{r\dar0}\int_{\g_+}\frac{e^{izy}}{z+a}\frac1{z-a}\,dz
=\lim_{z\to a}\frac{e^{izy}}{z+a}\,i\pi
=\frac1{2a}\pi ie^{iay}
$$
und analog folgt für $\g_-(t)\colon=-a+re^{it}$, $t\in(0,\pi)$:
$$
\lim_{r\dar0}\int_{\g_-}\frac{e^{izy}}{z^2-a^2}\,dz=-\frac1{2a}\pi ie^{-iay}
$$
Für $y > 0$ erhalten wir somit nach der Cauchyschen Integralformel:
$$
\pv\int_\R\frac{e^{ixy}}{x^2-a^2}\,dx
=\frac{-\pi}{a}\sin(ay)~.
$$
Für $y < 0$ z.B. nach dem Residuensatz angewandt auf den in die untere Halbebene $[\Im z < 0]$ ergänzten Integrationsweg (oder aufgrund der Symmetrie):
$$
\pv\int_\R\frac{e^{ixy}}{x^2-a^2}\,dx
=\frac{\pi}{a}\sin(ay)~.
$$
2. Die (distributionelle) Fourier-Transformierte der Funktion $f(x)=1/x$ ist gegeben durch
$$
\wh f(y)
=-i\pi\sign(y)/\sqrt{2\pi}
=-i\sqrt{\pi/2}\sign(y)~.
$$
Für $y < 0$ ist $\pv\int_\R e^{-ixy}/x\,dx=i\pi$ und da $f$ ungerade ist, folgt die behauptete Beziehung.
Digression: Distributional Fourier transform
Weder die Funktion $1/(x^2-a^2)$ noch die Funktion $1/x$ sind auf $\R$ lokal integrierbar. Die Fourier-Transformierte dieser Funktionen haben wir daher durch den Cauchyschen Hauptwert definiert - falls dieser existiert! Allgemeiner ist die distributionelle Fourier-Transformierte einer z.B. lokal integrierbaren Funktion $f:\R^n\rar\C$ definiert (vgl. Parsevalsche Gleichung):
$$
\forall\vp\in C_c^\infty(\R):\quad
\int f(x)\wh\vp(x)\,dx
=\int\wh f(y)\vp(y)\,dy~.
$$
Eine solche Funktion $\wh f$ muß jedoch nicht existieren; z.B. für die konstante Funktion $f(x)=1$, denn in diesem Fall müßte gelten: $\int\wh f(y)\vp(y)\,dy=\int\wh\vp(x)\,dx=c_1^{-1}\vp(0)$; eine solche Funktion $\wh f$ gibt es aber nicht! Es gibt jedoch ein Maß - nämlich das im Punkt $0$ konzentrierte Diracmaß $\d_0$ multipliziert mit $c_1^{-1}$. Analog kann man $c_1^{-1}\d_y$ als die distributionelle Fourier-Transformierte der Funktion $x\mapsto e^{ixy}$ betrachten, denn
$$
\int\vp(x)\,c_1^{-1}\d_y(dx)
=c_1^{-1}\vp(y)
=\int e^{ixy}\wh\vp(x)\,dx
$$
Wir wollen uns im Weiteren jedoch auf Funktionen $\wh f$ beschränken. Proposition besagt z.B., daß für ein $l$-homogenes harmonisches Polynom $H$ in $\R^n$ die distributionelle Fourier-Transformierte der Funktion $x\mapsto H(x)\Vert x\Vert^{-l-n+\a}$ bis auf einen Faktor mit der Funktion $x\mapsto H(x)\Vert x\Vert^{-l-\a}$ übereinstimmt.
Falls $f$ quadratisch integrierbar ist, dann stimmt die distributionelle Fourier-Transformierte mit der üblichen Fourier-Transformierten überein! Im Rahmen der Theorie der Distributionen definiert man die Fourier-Transformation auf viel allgemeineren Objekten denn Funktionen (cf. e.g. J. Alvarez). Wir wollen das hier für Funktionen $f$ ausführen, die mit Ausnahme endlich viele Punkte $E$ auf der erweiterten reellen Achse $\cl{\R}$ lokal integrierbar sein sollen.
Angenommen $f:\cl{\R}\sm E\rar\R$ sei mit Ausnahme endlich viele Punkte $E$ lokal integrierbar und für alle $\vp\in C_c^\infty(\R)\cup\F(C_c^\infty(\R))$ existiere der Cauchysche Hauptwert:
$$
\pv f(\vp)
\colon=\lim_{r\dar0}\int_{E_r^c}\vp(x)f(x)\,dx
=\pv\int_\R\vp(x)f(x)\,dx~.
$$
Dies gilt z.B. wenn $f$ nur Pole erster Ordnung besitzt und ein $n\in\N_0$ existiert, so daß $\lim_{x\to\pm\infty}f(x)/|x|^n=0$ (cf. e.g. Beispiel. Existiert eine Funktion $\wh f$, so daß für alle $\vp$:
$$
\pv f(\wh\vp)=\int\vp(x)\wh f(x)\,dx,
$$
so nennt man $\wh f$ die distributionelle Fourier-Transformierte von $f$. Im Unterschied zur Definition der distributionellen Fourier-Transformierten einer lokal integrierbaren Funktion steht also auf der linken Seite der Cauchysche Hauptwert! Jedenfalls erhalten wir
\begin{eqnarray*}
\pv f(\wh\vp)
&=&\pv\int_\R\wh\vp(y)f(y)\,dy
=\lim_{r\dar0}\int_{E_r^c}\wh\vp(y)f(y)\,dy\\
&=&c_1\lim_{r\dar0}\int_{E_r^c}\int_\R\vp(x)e^{-ixy}f(y)\,dx\,dy
=\lim_{r\dar0}\int_\R\vp(x)c_1\int_{E_r^c}f(y)e^{-ixy}\,dy\,dx~.
\end{eqnarray*}
Falls nun erstens der Cauchysche Hauptwert
\begin{equation}\label{arteq12}\tag{ART12}
\wh f(x)\colon=c_1\lim_{r\dar0}\int_{E_r^c}f(y)e^{-ixy}\,dy
\end{equation}
existiert und zweitens $C > 0$ und $n\in\N_0$ existieren, so daß für alle $r > 0$:
$$
\Big|c_1\int_{E_r^c}f(y)e^{-ixy}\,dy\Big|\leq C(1+|x|^n),
$$
dann folgt $|\wh f(x)|\leq C(1+|x|^n)$ und
$$
\pv\int_\R f(x)\wh\vp(x)\,dx
=\pv f(\wh\vp)
=\int_\R\wh f(x)\vp(x)\,dx~.
$$
Daher ist durch \eqref{arteq12} tatsächlich die distributionelle Fourier-Transformierte von $f$ definiert.
Bemerkung: Da $\F(C_c^\infty(\R))$ nicht in $C_c^\infty(\R)$ enthalten ist, ist es günstiger die distributionelle Fourier-Transformation auf einem etwas erweiterten Raum zu betrachten, dem Schwartzraum, cf. e.g. Abschnitt oder wikipedia.
Für alle $r > 0$:
$$
c_1\int_{-r}^r\sign(y)e^{-ixy}\,dy
=ic_1x^{-1}(-1+e^{ixr}+e^{-ixr}-1)
=2ic_1x^{-1}(\cos(rx)-1)
$$
und der Limes $\lim_{r\to\infty}(\cos(rx)-1)$ existiert nicht.
Das nachstehende Beispiel zeigt, daß die Bildung des Cauchyschen Hauptwerts i.W. nur bei Integranden mit einfachen Polstellen sinnvoll ist:
Für welche $x > 0$ und $n\in\N$, $n\geq2$, existiert der Cauchysche Hauptwert (
Lösungsvorschlag)
$$
\pv\int_\R\frac{e^{ixy}}{(1-x)^n}\,dx?
$$
Hilbert transform on $\R$
Sei $f:\R\rar\C$ meßbar. Falls der Cauchysche Hauptwert existiert, dann nennt man die durch
$$
Hf(x)\colon=\frac{1}{\pi}\pv\int_\R\frac{f(y)}{x-y}\,dy~.
$$
definierte Funktion $Hf$ die Hilbert-Transformierte - $Hf$ stimmt also mit der 'Faltung' $h*f$ überein, wobei $h(x)=1/\pi x$. Die wesentlichste Eigenschaft der Hilbert-Transformation ist aber folgende: bezeichnen $u$ bzw. $\wt u$ die harmonischen Fortsetzungen von $f:\R\rar\R$ bzw. $Hf:\R\rar\R$ in die obere Halbebene $H^+\colon=[\Im z > 0]$, so ist $F\colon=u+i\wt u$ komplex differenzierbar. Gleichbedeutend damit ist die Eigenschaft, daß die Fourier-Transformierte von $f+iHf$ auf der negativen reellen Achse verschwindet - Physiker sagen dazu: die Funktion $f+iHf$ besitzt nur positive Frequenzen.
Sei $a > 0$ und $\g_+$ der Halbkreis $\g_+(t)=x+re^{it}$, $0 < t < \pi$, dann erhalten wir:
$$
\lim_{r\dar0}\int_{\g_+}\frac{e^{iaz}}{x-z}\,dz
=-i\lim_{r\dar0}\int_0^{\pi}e^{ia(x+re^{it})}\,dt
=-\pi ie^{iax}~.
$$
Es folgt daher nach der Cauchyschen Integralformel:
$$
\pv\int_\R\frac{e^{iay}}{x-y}\,dy+\pi ie^{iax}=0
$$
Sei z.B. $f(x)=\cos x$, dann ist $Hf(x)=-i(e^{ix}-e^{-ix})/2=\sin x$ und $f(x)+iHf(x)=e^{ix}$ ist die Einschränkung der komplex differenzierbaren Funktion $F(z)=e^{iz}$ auf die reelle Achse!
Die distributionelle Fourier-Transformierte von $h(x)=1/x$ ist nach Unterabschnitt: $\wh h(y)=-i\sign(y)/\sqrt{2\pi}$, also wegen $\F(h*f)=\sqrt{2\pi}\wh h\cdot\wh f$:
$$
\F(Hf)(y)
=\F(h*f)(y)
=\sqrt{2\pi}\wh h(y)\wh f(y)
=-i\sign(y)\wh f(y)~.
$$
Die Nullstellen von $g(z)\colon=1+z^{2m}$ in $[\Im z > 0]$ sind $z_k\colon=e^{(2k+1)\pi i/2m}$, $k=0,1,\ldots,m-1$. Damit folgt:
$$
\Res(z_k,\frac{f(z)}{z-x})
=\frac1{g^\prime(z_k)(z_k-x)}
=\frac1{2mz_k^{2m-1}(z_k-x)}
=\frac1{2m(-1-z_k^{2m-1}x)}
=\frac1{2m(-1+e^{-(2k+1)\pi i/2m}x)}
$$
und wir erhalten
$$
Hf(x)
=-if(x)+\frac{i}{m}\sum_{k=0}^{m-1}\frac1{e^{-(2k+1)\pi i/2m}x-1}
$$
Partial fraction and product formulas
Wie bereits im Falle der Bernoulli-Polynome nutzen wir auch hier den Residuensatz um eine Summe mithilfe eines Integrals zu berechnen: Sei $p$ eine Polynomfunktion mit $d\colon=\deg(p)\geq2$ und den Nullstellen $N\sbe\C$, so daß keine Nullstelle von $p$ in $\Z$ liegt. Ist dann $C_n$ das Quadrat mit den Eckpunkten $(n+1/2)(1+i),(n+1/2)(-1+i),(n+1/2)(-1-i)$ und $(n+1/2)(1-i)$, so liegen erstens (für hinreichend große $n$) alle Nullstellen von $p$ in $C_n$ und zweitens gilt für alle $z\in C_n^c$: $|p(z)|\geq K|z|^d$. Sei
$$
f(z)\colon=\frac1{p(z)\sin(\pi z)},
$$
dann folgt nach dem Residuensatz:
$$
\int_{\pa C_n}f(z)\,dz
=2\pi i\sum_{w\in C_n}\Res(w,f)
$$
Da $d\geq2$ und für $x,y\in\R$: $|\sin(x+iy)|^2=\sin^2(x)+\sinh^2(y)$, konvergieren die Integrale auf allen vier Seiten von $C_n$ mit $n\to\infty$ gegen $0$; es gilt also:
$$
0=\lim_{n\to\infty}\sum_{w\in C_n}\Res(w,f)
$$
In $z=k\in\Z$ besitzt $f$ das Residuum
$1/(p(k)\pi\cos(k\pi))=(-1)^k/(\pi p(k))$, also:
\begin{equation}\label{arteq13}\tag{ART13}
\lim_{n\to\infty}\sum_{|k| < n}\frac{(-1)^k}{\pi p(k)}
=-\sum_{w\in N}\Res(w,f)
\end{equation}
Sei insbesondere $p(z)=z^2-w^2$ mit $w\notin\Z$, dann ist $N=\{\pm w\}$ und
$$
\sum_{z\in N}\Res(z,f)
=\frac1{w\sin(\pi w)}~;
$$
damit erhalten wir die sogenannte Partialbruchzerlegung von
$\pi/w\sin(\pi w)$:
\begin{equation}\label{arteq14}\tag{ART14}
-\sum_{k\in\Z}\frac{(-1)^k}{k^2-w^2}
=\frac{\pi}{w\sin(\pi w)}~.
\end{equation}
Ersetzt man in der Definition von $f$ $\sin(\pi z)$ durch $\tan(\pi z)$, so folgt aus
$$
|\tan(x+iy)|^2=\frac{\sin^2(x)+\sinh^2(y)}{\cos^2(x)+\sinh^2(y)},
$$
daß $|\tan(\pi z)|^2$ auf $\pa C_n$ nach unten beschränkt ist durch $1/2$. Da das Residuum von $1/(z^2-w^2)\tan(\pi z)$ im Punkt $z=k$ gleich $1/(k^2-w^2)\pi/\cos^2(\pi z)$, erhält man die Partialbruchzerlegung von $\pi/w\tan(\pi w)$:
\begin{equation}\label{arteq15}\tag{ART15}
-\sum_{k\in\Z}\frac1{k^2-w^2}
=\frac{\pi}{w\tan(\pi w)}~.
\end{equation}
Nun ist $w\mapsto\pi/\tan(\pi w)$ die Ableitung von $f:w\mapsto\log\sin(\pi w)$, also:
$$
f^\prime(w)
=\frac{\pi}{\tan(\pi w)}
=\frac1{w}-\sum_{k=1}^\infty\frac{2w}{k^2-w^2}
=\log^\prime w+\sum_{k=1}^\infty(\log f_k)^\prime(w)
$$
wobei für $k\in\N$: $f_k(w)\colon=1-w^2/k^2$. Es gibt daher eine Konstante $C\in\C$, so daß für alle $w\in\C\sm\Z$:
$$
\log\sin(\pi w)=C+\log w+\sum_{k=1}^\infty\log\Big(1-\frac{w^2}{k^2}\Big)
$$
Aus $\lim_{w\to0}\sin(\pi w)/w=\pi$ schließen wir: $C=\log\pi$. Somit haben wir die Eulersche Produktdarstellung der Sinusfunktion:
\begin{equation}\label{arteq16}\tag{ART16}
\sin(\pi w)=\pi w\prod_{k=1}^\infty\Big(1-\frac{w^2}{k^2}\Big)~.
\end{equation}
Mithilfe der Produktdarstellung der Gammafunktion (cf. Abschnitt)
erhalten wir daraus unmittelbar die Ergänzungsformel der Gammafunktion:
\begin{equation}\label{arteq17}\tag{ART17}
\frac1{\G(z)\G(-z)}=-\frac{z\sin(\pi z)}{\pi}\quad\mbox{i.e.}\quad
\frac1{\G(z)\G(1-z)}=\frac{\sin(\pi z)}{\pi}~.
\end{equation}

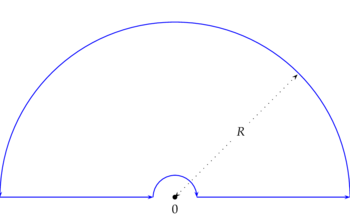
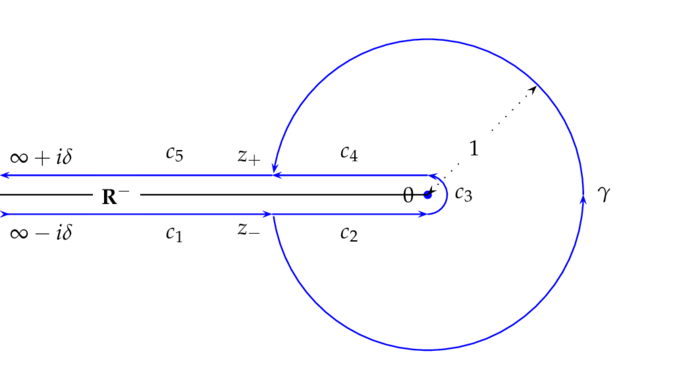
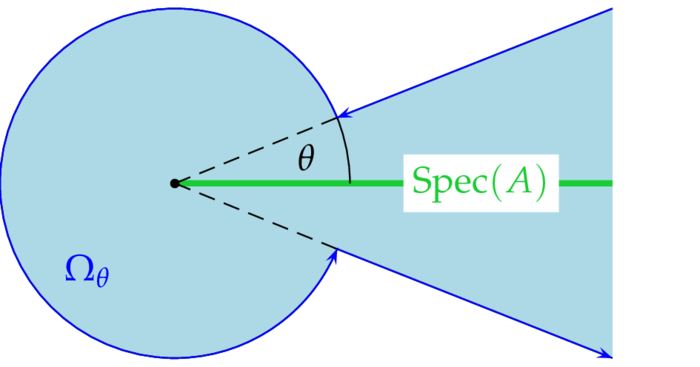 Damit die Funktion $z\mapsto e^{-wz}$ im Unendlichen verschwindet müssen wir $z$ so wählen, daß $|\arg(w)+\arg(z)| < \pi/2$. Sei daher $\theta\in(\a,\pi/2-|\arg(w)|)$, also insbesondere: $|\arg(w)| < \pi/2-\a$. Ferner setzen wir:
$$
\O_\theta\colon=S_\theta\cup\cl D=\{z\in\C:|\arg(z)|\leq\theta\}\cup\cl D~.
$$
Bezeichnet $\g_n$ eine Parametrisierung jenes Teils von $\pa\O_\theta$, der von $ne^{i\theta}$ gegen den Uhrzeigersinn nach $ne^{-i\theta}$ verläuft, so setzen wir $\g\colon=\g_\infty$ und
$$
P_w\colon=\lim_n\frac1{2\pi i}\int_{\g_n} e^{-wz}U_z\,dz
=\frac1{2\pi i}\int_{\g} e^{-wz}U_z\,dz
$$
1. Die Definition ist unabhängig von $\theta\in(\a,\pi/2-|\arg(w)|)$: Nach dem Cauchyschen Integralsatz genügt der Nachweis, daß für $\a < \theta_0 < \theta_1 < \pi/2-|\arg(w)|$:
$$
\lim_n\norm{\int_{c_n}e^{-zw}U_z\,dw}=0,
$$
wobei $c_n$ die beiden Kreisbögen zwischen $ne^{i\theta_1}$ und $ne^{i\theta_0}$ bzw. zwischen $ne^{-i\theta_0}$ und $ne^{-i\theta_1}$ bezeichnet. Nun ist für ein $\d > 0$: $\theta_1+|\arg(z)|\leq\pi/2-\d$ und damit nach Voraussetzung:
$$
\int_0^1
|e^{-zc_n(t)}|
\Vert(c_n(t)+A)^{-1}\Vert|c_n^\prime(t)|\,dt
\leq e^{-n\cos(\pi/2-\d)}
\frac{C_{\theta_0}}n2n(\theta_1-\theta_0)~.
$$
2. Wir zeigen nun analog zum Spektralkalkül, daß $P_w$ eine Halbgruppe ist; dazu benötigen wir wiederum die Resolventengleichung \eqref{asceq3}: Seien für $j=0,1$: $\g_j\colon=\pa\O_{\theta_j}$ - aus technischen Gründen sollten wir in der Definition von $\O_\theta$ anstelle von $D$ eine Kreisscheibe wählen, die mit $\theta$ strikt wächst, also etwa $D$ durch $D_{1+\theta}$ ersetzen:
\begin{eqnarray*}
P_{w_1}P_{w_0}
&=&-\frac1{4\pi^2}\int_{\g_1}\int_{\g_0}
e^{-z_1w_1-z_0w_0}U_{z_1}U_{z_0}\,dz_0\,dz_1\\
&=&-\frac1{4\pi^2}\int_{\g_1}\int_{\g_0}
\frac{e^{-z_1w_1-z_0w_0}}{z_1-z_0}(U_{z_0}-U_{z_1})\,dz_0\,dz_1\\
&=&-\frac1{4\pi^2}\int_{\g_0}\Big(\int_{\g_1}
\frac{e^{-z_1w_1-z_0w_0}}{z_1-z_0}\,dz_1\Big)U_{z_0}\,dz_0
+\frac1{4\pi^2}\int_{\g_1}\Big(\int_{\g_0}
\frac{e^{-z_1w_1-z_0w_0}}{z_1-z_0}\,dz_0\Big)U_{z_1}\,dz_1
\end{eqnarray*}
Wählen wir wiederum den Winkel $\theta_1$ von $\g_1$ größer als den Winkel $\theta_0$ von $\g_0$, so folgt aus der Cauchyschen Integralformel sowie einer zu Beispiel analogen Rechnung: das zweite innere Integral verschwindet und für das erste Doppelintegral erhalten wir
$$
\frac1{2\pi i}\int_{\g_0}
e^{-z_0w_0-z_0w_1}U_{z_0}\,dz_0
=P_{w_0+w_1}~.
$$
Damit die Funktion $z\mapsto e^{-wz}$ im Unendlichen verschwindet müssen wir $z$ so wählen, daß $|\arg(w)+\arg(z)| < \pi/2$. Sei daher $\theta\in(\a,\pi/2-|\arg(w)|)$, also insbesondere: $|\arg(w)| < \pi/2-\a$. Ferner setzen wir:
$$
\O_\theta\colon=S_\theta\cup\cl D=\{z\in\C:|\arg(z)|\leq\theta\}\cup\cl D~.
$$
Bezeichnet $\g_n$ eine Parametrisierung jenes Teils von $\pa\O_\theta$, der von $ne^{i\theta}$ gegen den Uhrzeigersinn nach $ne^{-i\theta}$ verläuft, so setzen wir $\g\colon=\g_\infty$ und
$$
P_w\colon=\lim_n\frac1{2\pi i}\int_{\g_n} e^{-wz}U_z\,dz
=\frac1{2\pi i}\int_{\g} e^{-wz}U_z\,dz
$$
1. Die Definition ist unabhängig von $\theta\in(\a,\pi/2-|\arg(w)|)$: Nach dem Cauchyschen Integralsatz genügt der Nachweis, daß für $\a < \theta_0 < \theta_1 < \pi/2-|\arg(w)|$:
$$
\lim_n\norm{\int_{c_n}e^{-zw}U_z\,dw}=0,
$$
wobei $c_n$ die beiden Kreisbögen zwischen $ne^{i\theta_1}$ und $ne^{i\theta_0}$ bzw. zwischen $ne^{-i\theta_0}$ und $ne^{-i\theta_1}$ bezeichnet. Nun ist für ein $\d > 0$: $\theta_1+|\arg(z)|\leq\pi/2-\d$ und damit nach Voraussetzung:
$$
\int_0^1
|e^{-zc_n(t)}|
\Vert(c_n(t)+A)^{-1}\Vert|c_n^\prime(t)|\,dt
\leq e^{-n\cos(\pi/2-\d)}
\frac{C_{\theta_0}}n2n(\theta_1-\theta_0)~.
$$
2. Wir zeigen nun analog zum Spektralkalkül, daß $P_w$ eine Halbgruppe ist; dazu benötigen wir wiederum die Resolventengleichung \eqref{asceq3}: Seien für $j=0,1$: $\g_j\colon=\pa\O_{\theta_j}$ - aus technischen Gründen sollten wir in der Definition von $\O_\theta$ anstelle von $D$ eine Kreisscheibe wählen, die mit $\theta$ strikt wächst, also etwa $D$ durch $D_{1+\theta}$ ersetzen:
\begin{eqnarray*}
P_{w_1}P_{w_0}
&=&-\frac1{4\pi^2}\int_{\g_1}\int_{\g_0}
e^{-z_1w_1-z_0w_0}U_{z_1}U_{z_0}\,dz_0\,dz_1\\
&=&-\frac1{4\pi^2}\int_{\g_1}\int_{\g_0}
\frac{e^{-z_1w_1-z_0w_0}}{z_1-z_0}(U_{z_0}-U_{z_1})\,dz_0\,dz_1\\
&=&-\frac1{4\pi^2}\int_{\g_0}\Big(\int_{\g_1}
\frac{e^{-z_1w_1-z_0w_0}}{z_1-z_0}\,dz_1\Big)U_{z_0}\,dz_0
+\frac1{4\pi^2}\int_{\g_1}\Big(\int_{\g_0}
\frac{e^{-z_1w_1-z_0w_0}}{z_1-z_0}\,dz_0\Big)U_{z_1}\,dz_1
\end{eqnarray*}
Wählen wir wiederum den Winkel $\theta_1$ von $\g_1$ größer als den Winkel $\theta_0$ von $\g_0$, so folgt aus der Cauchyschen Integralformel sowie einer zu Beispiel analogen Rechnung: das zweite innere Integral verschwindet und für das erste Doppelintegral erhalten wir
$$
\frac1{2\pi i}\int_{\g_0}
e^{-z_0w_0-z_0w_1}U_{z_0}\,dz_0
=P_{w_0+w_1}~.
$$